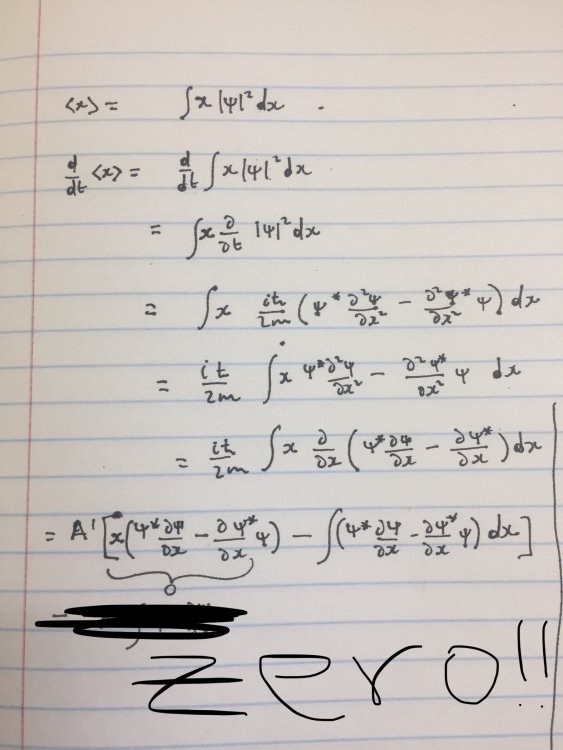Leaderboard

No. They are purely about the "completeness" of formal systems. In other words, can a formal system (e.g. mathematics) prove that anything that can be written down using that formal system is either true of false. And the answer to that is no. You can write something using mathematics that you cannot use the same mathematics to prove or disprove. You can extend your formal system to make it more complete and allow you to prove that statement. But then there will be other statements that this extended system cannot prove. And so ad infinitum. Physics uses mathematics but it is not limited by that mathematics in the same way. (And some mathematicians complain that physicists are a bit "ad hoc" and don't really stick to absolutely formal derivations.)

That is out of my knowledge. The only thing I can say is that trying to change the elements (river, sea, land) in a specific way most of the times drive to unexpected results. I have the experience where a hotel constructed a small dock in the sea for his single inflated boat sportcraft had the result to erase completely its sandy beach.

Please show me how to move from equation 1.30 to 1.31 I tried using integration by parts

Pretty much everything in mathematics can be proved. There are a few well-known problems that have not been proved yet (some have substantial prizes associated with them). It took over 300 years before someone proved Fermat's Last Theorem. That is partly because it had to build on a huge amount of mathematics that was developed in the meantime. Some very simple looking problems can be very hard to solve. Some quite complex sounding problems, that people have struggled with for decades, might turn out to have a really simple proof. (Mathematics is one of the few files where outsiders can, and do, make breakthroughs.) There are lots of unknowns in mathematics (e.g the continuum hypothesis; that there is no infinity between the (infinite) set of integers and the (infinitely larger) set of reals) that have not yet been proved either way. And there are some problems for which it can be proved that there's no solution. But I don't think you can ever say that a particular problem is unprovable because of Gödel Incompleteness. Unless it is a problem specifically constructed to be unprovable for that reason (which is how Gödel proved the theorem; by constructing a mathematical statement that could not be proved in the rules of the system).

Yes Strange's description of 'formal systems' is a good one. And whilst much of mathematics is embodied in formal systems some important parts are not. For instance the technique of iterative refinement is widely used in Science and Engineering. That is Have a guess at the answer or value you seek. Substitute in your guesstimate and see how close to the correct outcome you are. Refine your first guess and test again. Repeat until your guess matches observation to the required degree of accuracy. This technique appears in statistics as Bayes Theorem. Remember that in Physics well conducted observation always trumps any 'proof' or theoretical determination of a result.

Symmetric is the term your looking or in this case also commutative. (Under constant velocity) This is shown as the inner product of the Minkowskii group is symmetric via [math]\mu \cdot \nu=\nu \cdot \mu[/math] The equations are linearized however that doesn't necessarily describe reversible functions.

I have a copy of his second edition. It's a decent textbook. Griffith has a section on Dirac notation.

I think I can do a little bit more than that. Most, if not all, interesting wave functions in QM have a behaviour that goes to zero as a Gaussian at infinity. If you take a look at most eigenfunctions of "realistic"* Hamiltonians, for example, the harmonic oscillator, hydrogen atom, etc. The all are dominated by exponential damping at infinity. Example: \[\psi\left(x,0\right)=\frac{e^{-x^{2}/2-if\left(x\right)}}{x^{n}}\] Now it's very easy to see that no matter what power of x is integrated against the exponential, the idea works. \[\int_{\mathbb{R}}dx\frac{e^{-x^{2}/2+if\left(x\right)}}{x^{n}}\frac{d}{dx}\left[\frac{e^{-x^{2}/2-if\left(x\right)}}{x^{n}}\right]=\left.\frac{e^{-x^{2}}}{x^{2n}}\right|_{-\infty}^{+\infty}-\int_{\mathbb{R}}dx\frac{d}{dx}\left[\frac{e^{-x^{2}/2+if\left(x\right)}}{x^{n}}\right]\frac{e^{-x^{2}/2-if\left(x\right)}}{x^{n}}\] Watch out for silly mistakes. * Meaning nothing pathological, like Airy functions, or something like that.

No, no. Careful. That's not the point. The point is that the integrals, \[\int dx-\left(\frac{\partial\psi^{*}}{\partial x}\psi\right)\] and, \[\int dx\psi^{*}\frac{\partial\psi}{\partial x}\] differ in what is called "a surface term" or "a boundary term". Because in quantum mechanics the boundary is at infinity, they can be identified for all intents and purposes. If you equate one of these integrals to its complex conjugate, what you're saying is that the integral is real. That's not quite so correct. The integrals are equal except terms that vanish at infinity. The point is a bit subtle, but that's the way to read its meaning. Edit: In this case, the surface term is, \[\left.\left(\psi^{*}\psi\right)\right|_{\textrm{infinity}}\]

Consider: \[\int dx\left(-\frac{\partial\psi^{*}}{\partial x}\psi\right)=\int dx\psi^{*}\frac{\partial\psi}{\partial x}\] and what I told you in the other post about fields vanishing fast enough at infinity. You get twice the first integral in 1.30.

How was the equation highlighted in the attachment below simplified. I get the other term but another highlighted term went to zero, how? The hand writing is where I tried using integration by parts. A’ = ih/2m

It is because you are evaluating the integral at the limits of integration. That's very common in any field theory. The fields are assumed to go to zero fast enough at infinity. In fact, you need that if you want your momentum operator to be Hermitian. If D is any of these differential operators, you need both the i and the vanishing at infinity so that, \[\int d^{3}xF^{*}iD\left(G\right)=\int d^{3}x-\left(DF^{*}\right)iG=\] \[=\int d^{3}x\left(iDF\right)^{*}iG\] I hope that helps. Good question. +1

So basically you’re suggesting we can only fix this problem by hiring members of the Gracie family to police our streets? Seems unrealistic, but okay. I think more is needed, like federally set bare minimum standards about what is and is not allowed and what happens when those thresholds are crossed. The defund the police objective is a poorly framed way of asking for funds to be out to better uses. It’s not at odds, it’s exactly what they’re seeking. Yes, who wouldn’t? But why present a false choice / false dichotomy? It’s not like those are the only 2 options available. They could also buy me a cheeseburger or get me engaged with a social worker.

No choke holds. Full stop. Blood choke. Air choke. Artichoke. It doesn’t matter. If you’re a cop you don’t choke others. That has to be one of the rules of engagement. We’re citizens with rights in a free society. We’re not willing fighters entering an octagon for a paycheck.

Thank you for the detailed answers. +1 You mean lambda = 1+ √5 And lambda = 4 is the chaotic one.

Good that you are still with us after all that squabbling. Please explain where you got those ideas post a link or reference. Because they are seditious. The whole point of Maths is that it is self consistent. But that does not mean that any part of it is complete ie tells everything. That is the point of Godel's incompleteness theorems - we will never know everything unless everything is limited. But we do not know and I do not believe that 'everything is limited'. If you like ? a bit of background about the Erlangen program and David Hilbert might help place Godel in context.

Just to add to that, it's not like in SR where each observer also has a different notion of simultaneity, but each of those is physically meaningful. Eg. in flat spacetime, any two events that can be considered simultaneous by someone will have intersecting future light cones, where different future observers can agree or disagree on whether the events were simultaneous. In GR you must make a choice of how to define the surfaces of a foliation, that's not just based on a physically meaningful connection between its events. You'd choose it to make a useful tool, not a 'real' representation of simultaneity throughout the universe for a given observer.

Not a bad idea at all. I was breeding on such a 'pin' for philosophy. I would like to see similar requirements to postings in other groups, so: opinions without (good?) arguments are not acceptable Questions, except completely nonsensical ("What is the colour of time?") are of course allowed Taking away some misunderstandings about what philosophy is (not wild speculations, not scientific speculations, but intelligibility problems) I can try to write such a 'pinned post'. Of course I also think about a pinned post about free will... I think I can express me pretty neutrally. (Living in Switzerland for nearly 30 years now )

As noted, this works in principle (just isn’t very effective in practice - although light sails may be). But I am curious why you think it would require space to have drag for it to work? Are you thinking that the light would need to push against something? But that is not how propulsion works - otherwise rockets would not work in space! It is enough that the light pushes against the spacecraft (as it leaves). Physics 🙂