Leaderboard

Ok, I get you now. This is not a trivial question, and the short truth is that we do not really know the answer, based on currently known physics. The trouble is this - the established model currently available to describe gravity (General Relativity, or GR for short) is purely classical, meaning it does not and cannot account for quantum effects. When we describe the process of gravitational collapse, then in the beginning stages of that process quantum effects can be neglected, so up to a certain point GR does a really good job in describing things. We can even cheat a bit, and extend the range for which our description is valid by considering already known quantum effects simply as classical pressures that counteract gravity. For suitable initial conditions, this may yield an equilibrium state such as a dwarf star, or a neutron star, or something more exotic like quark stars. However, once the total mass of the collapsing object exceeds a certain limit, there is no known mechanism by which the collapse could be stopped - in these cases the object keeps collapsing under its own gravity, and eventually becomes so dense that quantum gravitational effects can no longer be ignored. At that point General Relativity quite simply stops being a valid model. And this is where we get stuck, because we do not yet have a model of quantum gravity, so we simply do not know what happens in the final stages of such a collapse, and what happens to the mass of the original object. There are a few speculations, hypotheses and candidate models, but none of them is sufficiently well understood, or tested in any way. If we naively consider GR on its own, the end result of this collapse is a singularity - all the mass of the collapsing object becomes concentrated in a single point of infinite density, and infinite spacetime curvature. The ‘size’ of that infinity is always zero, regardless of how much mass you start out with, and regardless of how much mass falls into it later on. However, this is not to be understood as a physical prediction - in physics, when a model becomes singular and infinite, then that simply means that we have wrongly extended that model beyond its domain of applicability. In this particular case, we have attempted to apply a purely classical model to a physical situation that is decidedly not classical, so obviously the answer we get is not physically meaningful. Note that the singularity itself, for mathematical reasons, wouldn’t be part of the spacetime manifold, so counterintuitively the entire spacetime in and around a black hole of this kind would be completely empty. The mass of such a black hole is actually a global property of the entire spacetime, and cannot be localised anywhere. The volume of a singularity - in so far as that concept makes sense (it doesn’t, really) is zero. This is true for both point singularities, and ring singularities. Yes, in the purely classical picture of GR it would be matter compressed to infinite density. But we know (see above) that this is not a physical meaningful concept, since it cannot happen in the real universe. Even the already known laws of quantum physics prohibit such a state (ref e.g. the Pauli exclusion principle). Again, in the classical picture of GR the answer is no - the singularity remains point-like or ring-like. What does change though is the radius of the event horizon. When we look at current attempts to write out a model of quantum gravity (a very difficult problem!), then three main themes emerge, depending on which model is used: 1. Below a certain length scale, a new symmetry emerges that turns the collapse into a rebound - so the collapsing matter will never become singular, but instead begins to ‘bounce’ back out while the event horizon shrinks. However, due to the extreme time dilation in that region, this process would take a very long time (~100s of billions of years) as seen by an outside observer, which is why it has never been observed. 2. You end up with some sort of exotic degeneracy state below the horizon, such as a fuzzball. 3. Spacetime itself becomes quantised below a certain length scale, so the question as to what happens to the matter or where it goes becomes meaningless There is no telling at present if any of these possibilities describes what actually happens in the real world. Yes, but at the same time it will also continue to evaporate via Hawking radiation.

No, there are other ways to avoid the singularity - namely by making adjustments to the laws of (classical) gravity. The most straightforward amendment would be to allow what is called torsion in your spacetime. GR is explicitly constructed to use only curvature to describe gravity, so torsion always vanishes. If one allows torsion (simply by choosing a different connection), then we end up with a model called Einstein-Cartan gravity (ECG). In this model, the singularity never happens, and the collapse actually turns into a bounce, so after a very long time everything that fell into the black hole will bounce back out (but in scrambled form). This would also be true for the Big Bang singularity, so the BB model is naturally replaced by a ‘Big Bounce’ scenario. The issue with this is that when you allow torsion on your spacetime, then this has consequences not just for gravity, but for some other laws of physics as well - specifically, it makes the Dirac equation for spin-½ particles non-linear, and also has other impacts on the Standard Model. The resulting effects would be too small to be detectable at currently available energies (at least as far as I know), so ECG remains a potentially viable model that can’t be ruled out (but also not confirmed) at present. Yes, this is what would happen if String Theory is physically viable - the interior of black holes would then simply be the highest form of degeneracy, being what is called a fuzzball (see link in previous post). The singularity is again avoided. Well, instead of having a model of gravity that accounts for quantum effects, you can of course look for an extension of the Standard Model that accounts for gravitational effects. The end result is the same

Nothing to solve, as no problem has been posed.

Speaking as a licensed HIgh School math teacher I would say no-- not something we should teach in High School. Benford's law is indeed very interesting, but the High School math curriculum is focused on continuing the development of math skills started in lower grades, in a building block fashion, in order to prepare the student for post-HS education. Pre-Algebra, Algebra, Geometry, Algebra 2, pre-calc and sometimes early stages of Calculus. That is, we are still in the process of building connected competencies-- one topic building on the previous. Benford's law and its implications is pretty much outside the things that have to get done in High School. The amount of material to be mastered is very large and difficult to do as is-- I would not want to add more.

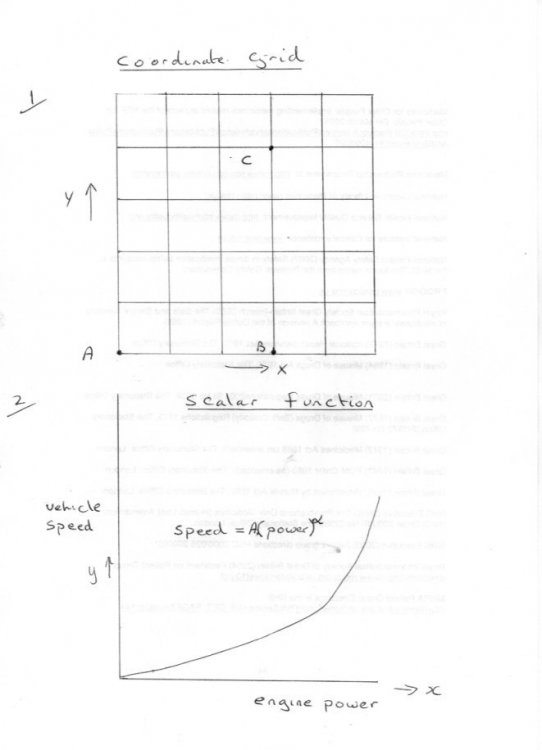
Swansont and Joe have both said more or less the same thing and given some examples. In particular there is a heirarchy or ladder; I have pointed out that vectors are not the top of the ladder. ...... Vectors Scalars Numbers So what are the differences and how do you tell these differences? It is a little more tricky than at first sight, as Joe has hinted since distance can be a scalar or a vector, depending upon circumstances. But let us start at the bottom. Numbers and scalars. Not all numbers are scalars. 3 and 5 by themselves are just numbers. You can add them together 3 + 5 = 8 Give them units eg 3 apples, 5 oranges. You cannot add these together 3 apples plus 5 oranges is always 3 apples plus 5 oranges (unless we rename them both fruit). You can, however add 3 apples and 5 apples to get 8 apples. So sometimes you can add scalars - but only if they ahae the same units and they apply to the same situation. 4 kg plus 4 kg is only 8 kg if they are on the same side of the scales. You can always add two any numbers to obtain a sum number without restriction Note swansont said scalars usually have units. Sometimes a scalar can be just a number. This is, in fact, where the name comes from, An enlargement of 1.2 or 120% on you photocopier is just a number, as is the scale factor on a map But adding the scale of one map to the scale of another makes no sense. And if you enlarge by 1.2 twice you do not get an enlargement of (1.2 + 1.2 =2.4) you get an enlargement of (1.2 * 1.2 = 1.44) So a number can be a scalar (one step up the ladder) or it can be just a number. Similarly Joe has noted that distance can be a scalar, with units, or it can be one step up the ladder as a vector. Talking of maps neatly brings us to coordinate systems where we can start to look at the differences between scalars and vectors. I assume you are familiar with plotting a graph of a function ? That is a form of coordinate system. We do not need fancy coordinates systems, a simple X - Y grid as in Fig 1will suffice. The important points are that X and Y are variables that on take on any value - that is we can choose any value for Y without regard to the value of X. So we can place A, B and C where we like on the grid. We say that X and Y are both independent variables and we need (at least) two of them to create a vector. Before we come to that, The graph plotted in fig 2 relates to swansont's example of speed and velocity. Both speed and power are scalars. The speed of our vehicle depends upon the power supplied by the engine. So we cannot place A, B and C anywhere on the XY plot we are constrained by the relationship between X and Y In this case we say that We say that X is an independent variable and Y is a dependent variables We will examine the significance of this when we come to plot vectors in the next instalment, along with the significance of the units of scalers for the addition of vectors. How are we doing?

The rotation isn’t in 3D Euclidean space, but in the 4D Minkowski spacetime of Special Relativity. The geometry of that spacetime is hyperbolic, so the situation is more complex than what can be easily visualised. Note also - and that is important - that spin is not a function of spacetime coordinates, so visualising it as some kind of rotation about itself is highly misleading. Rather, the rotation involved is one of the wavefunction about a hyperbolic angle in spacetime - in other words, a Lorentz transformation between inertial frames. I think a better way to understand spin is to take it to signify what kind of mathematical object the quantum mechanical wavefunction of the entity in question needs to be, in order for it to be compatible with both the laws of quantum mechanics and Special Relativity. Spin-0 means we are dealing with a scalar, spin-½ means it is a Dirac spinor (bispinor), spin-1 means it is a vector, and spin-2 means it is a rank-2 tensor. Of course all these object types are closely related, in that they are all representations of the Lorentz group - that group which captures the symmetries of spacetime. So spin is at its heart a relativistic phenomenon, and an expression of symmetry.

You are not invoking the function fun1(e) and storing the results in the list. You are storing five different functions fun1(e) in a list and never invoke them. Namely, the functions you store are fun1(e)=e+0, fun1(e)=e+1, fun1(e)=e+2, fun1(e)=e+3 and fun1(e)=e+4. What the print tells you is exactly this: Your list contains five functions named fun1 at the memory locations 0x7f6d8a364e18, 0x7f6d8a28a158 etc. If you wanted to invoke the function and store its values you'd need to invoke the function and type something like fun_list1.append(fun1(42)) (in this case you invoke it with the parameter 42 - every other number would work, too). And of course writing fun_list1.append(42 + j) would be the cleaner code to do the same without the unnecessary function. There are legitimate reasons why sometimes you want to store an actual function instead of the function result (you don't know the argument at the moment, you want to execute it multiple times, ....). You can call the stored function fun1(e) just like any other function. If you want to see evaluated results, change your print statement to print(x(42)) and your output should become 42, 43, 44, 45, 46 (again, the argument 42 is just a random number, and any other number should work).

On average, the OH bond will be polarised. In fact, it can participate in a particular type of dipole interaction called hydrogen bonding. As with all electrostatic interactions, it is not overly strong when you compare it to covalent bond strengths, but hydrogen bonds are considered quite a bit stronger than other intermolecular attractive forces. I have bolded a sentence that is not quite right. You won't covalently bond two ethane molecules together. You will get Van der Waals (also London dispersion forces) between molecules of ethane, but that's about it. They are very weak interactions. You will also get Van der Waals interactions with alcohol molecules. When you compare the two, you have (for example) ethanol, which has hydrogen bonding and Van der Waals interactions, and ethane, which only contains Van der Waals interactions. As you noted above, the stronger the interactions and the more of them that there are, the more energy it requires to break intermolecular bonds and pull molecules apart, which translates to a higher boiling point. As such, you would reasonably expect ethanol to have a higher boiling point to ethane. Another interesting comparison is between diethyl ether, acetic acid, ethanol and ethane. Can you predict the order of boiling points between those molecules from highest to lowest?

Yes, more or less. So with an alcohol, can you identify what sort of intermolecular interactions might exist? Hydrogen bonding, London dispersion, dipole, Van der Waals, etc.?