Leaderboard

I have seen some data and I can probably dig out papers for more detail. But from what I recall issues regarding substance abuse is fairly high, roughly in the 70% range. The most prominent one being alcohol. Mental illness depends a lot on classification, as substance abuse can also be classified as a disorder, for example. But diagnoses like schizophrenia, anxiety disorders and so on are fairly high and most long-term homeless folks suffer from something. Which is not surprising, as such. If not already suffering from these disorders, being homeless is certainly making things worse. But you are of course correct, one should really establish facts (rather than anecdotes) before thinking about doing something that can significantly affect other folks. Especially if the thing is convenient for you but with unclear consequences for others. The mere thought that it does not affect oneself, makes it easier to go way overboard, resulting in unintended atrocities.

Has the number of homeless who are addicts been established? Are we assuming most are? Or is addiction relatively rare among the homeless? I think it would help if we had some idea of what portion of homeless are addicts or mentally ill, or just people who are down and out financially.

The point is that you need to set the stage you are working on. That is the point of all the different offereings about open and closed sets, squences and so on. In what circumstances are you looking for a next number ? My stage is concerned with what are numbers? and what properties do we want them to have ? Thank you that I hope that is useful information to everybody. I expect he alsotold you that each Aleph is the cardinality of a particular infinite set of numbers. And perhaps he also made the point that it is not necessary for the cardinal number of the set to be an element of that set. I can be for finite sets, but it can't be for infinite sets. So often we all read something into what someone else has said, that was just not there. I do it, though I try to guard against it. In this case I specifically said the opposite To return to my stage. The thing about the rational numbers is that they have the same property we are examining as the reals, which is called density or denseness. Density should not be confused with completeness. In colloquial terms density means that between any two rational numbers we can find another rational number. This is an easy 3 line algebraic proof/demonstration if you want it. So the rationals also have this property of no nearest neighbour, assuming you have decided what you mean by 'nearest'. So what is the difference between the rationals and the reals ? Understanding this difference is the great step forward that Dedekind took when he published Stetigkeit und irrationale Zahlen, Braunschweig, in 1872 Yes WTF is correct in that Dedekind Cuts (Schnitt) divides the entire set of numbers into two subsets, but there is more to Dedekind than that. The fun begins when you try to determine which of the two sets a particular number belongs in. I was trying to avoid implying that 'isolating' every number in its own partition means just two partitions, I simply thought that perhaps you were half remembering something like this.

One example of all three is thermal equilibrium.

Removing a boundary point is akin removing surface from water. It is possible to remove a very thin layer of water from the surface, but it is not possible to remove the surface and to leave the water without a surface.

In my defence, I would suggest that there is a certain selection bias at play. I tend not to photograph those individuals I didn't notice.

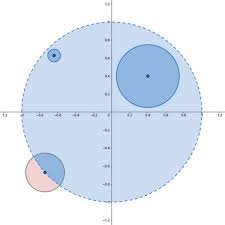
Thank you, glad it was helpful. After I wrote my post I went back and read through this entire thread, and I see I haven't actually said anything that hasn't already been said, so credit to all the others here before me. It's much more than that. It's a definitive proof that [math][0,1)[/math] has no largest element. Because if you claim that [math]x[/math] is the largest element, I can just note that [math]x + \frac{1 - x}{2}[/math] is strictly between [math]x[/math] and [math]1[/math]. I hope you can see that. This point was made by @Genady on page 1 of this thread. He noted that if p and q are real numbers then (p + q)/2 is a real number strictly between them. It's essentially the same argument that I just gave. Well it IS strange and interesting, that's why you asked! It is counterintuitive that given a real number, there is not a "next" point; and that if a line segment is missing its right endpoint, then it can't contain a largest number. Many people are confused about this, and it takes some understanding of the real numbers to correct our false intuitions. If it helps, think of the real numbers as maple syrup, or an infinitely stretchy rubber band; and not as a string of bowling balls. The real numbers are not lined up next to each other. Between any two real numbers are infinitely many more. Indeed, I just showed you a proof. Any candidate real number in [0, 1) that you might claim is the largest isn't. That's because you can take half the distance between your number and 1, and add it to x, to get a number strictly between your number and 1. It's a boundary point. That's one of the topological notions mentioned by @studiot on page 1. A boundary point has the property that any interval surrounding it necessarily contains points in the original interval, as well as points outside it. If you look at the closed unit interval [0,1] (remember that contains both endpoints) the right endpoint is indeed special. Any interval that contains it, such as, say, (.99, 1.01), contains points that are in [0,1] and also points not in [0,1]. That's the definition of a boundary point. A point in inside the interval, like 0.5, does not have that property. There are small intervals around 0.5 that are entirely contained within [0,1]. The name for that kind of point is interior point. So yes, boundary points are special. When you remove one of the endpoints from an interval, that end of the interval becomes open, and gets "fuzzy" if you think of it that way. It's sometimes more geometrically enlightening to think of it in two dimensions. Consider the unit disk consisting of all the points within 1 unit of the origin. If we include the boundary, we have the set [math]\{(x,y) : x^2 + y^2 \leq 1\}[/math]; and if we exclude the boundary, we have [math]\{(x,y) : x^2 + y^2 < 1\}[/math]. You can see that if we omit the boundary, for any point inside the disk, there's another point strictly between that point and the boundary. If we omit the boundary of the disk, there are no points that are "closest to the boundary." It gets fuzzy out there. Here's a picture I found online. You can see that a point on the boundary is characterized by the fact that any (blue and pink) disk we draw around it contains points of the original disk and points outside the disk. And any interior point is characterized by our ability to find a (blue) disk containing that point that's entirely within the original disk.

Meanwhile, mirror ribosome is on the way. https://www.science.org/doi/10.1126/science.abm0646 https://cen.acs.org/biological-chemistry/synthetic-biology/Mirror-image-polymerase-makes-key/100/web/2022/10

Correct. I have since amended that point as the discussion unfolded, the Sun Break Ranch proposal being more closely aligned with what I think would actually work.

I respect that you modified your ideas in the course of this chat, and it speaks to your openness to trying different things. I would guess that the above quote in the OP has, unfortunately, led to the recurrent references to guard towers, barb wire, and other validations of Godwin's Law of Net forums. As you realize by this point, the OP restriction above would necessitate guards of some kind, and physical barriers, given that some would opt to leave for whatever reason. I like the HF approaches, in that they recognize that any person, once they have a secure sheltering space over which they have some control, is better situated to consider how/if they might work on goals of betterment.

Look forward to seeing the 2040 ultra-stealthed furry-winged variation of the F35 fighter.

How about the Lorenz transformations ? They are equivalence relations. https://deepblue.lib.umich.edu/bitstream/handle/2027.42/152115/A_novel_equivalence_relation_in_relativity.pdf?sequence=1&isAllowed=y

Yes I agree it is about what one means by "real". I would contend that those calculational conveniences, and more importantly the concepts which we relate to one another in our calculations, do in the end purport to tell us something about physical existence, i.e. what we think is real, even if they do not claim to be definitive. Otherwise why bother? I think the scientist must believe there is an objective reality out there to be modelled, or he or she would not make the models. To borrow from St. Paul, we may "see through a glass darkly", but surely we have to think we are dimly perceiving something real, don't we?

Photons do not cause magnetic attraction. First, the classical EM field consists of very rapidly oscillating electric field, and an associated --also very rapidly oscilating-- magnetic field perpendicular to the E field, and both perpendicular to the direction of propagation of such EM field. Particles are predicted to oscillate in response by the theory, and so it is confirmed experimentally. That's how antennae work. It's oscillation, rather than overall attraction. Photons, OTOH, are quanta of such EM field. They can be absorbed, emitted, scatter... They never result in overall attraction either. They just change the state of electrically charged particles by making them change their energy and momentum. I hope that helps.

All electric charges possess an electric field around them. When they move their charge interacts with both their own electric field and the electric fields due to any other charges. Moving electric charges induce a magnetic field. We call this effect electromagnetism. This field changes according to the movement of the charges concerned. This distinguishes it from 'permanent magenetic' fields which do not change with movement (apart from moving bodily themselves with the magnet) But as Genady says the term is also used in a more general manner to cover all matter electrical and magnetic.

Hey everyone, I just wanted to share how the world looks to some people. To help me, I will be using Octavio Ocampo's paintings. Basically, some people see faces in almost everything.