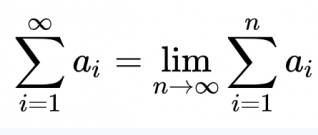Leaderboard

Step 1: The limit of the sequence 1/2, 3/4, 7/8/ 15/16, ... is 1 Step 2: The sum of an infinite series is defined as the limit of the sequence of partial sums. Step 3: The infinite series 1/2 + 1/4 + 1/8 + 1/16 + ... has the associated sequence of partial sums 1/2, 3/4, 7/8, 15/16, ... Step 4. Therefore the sum of the infinite series 1/2 + 1/4 + 1/8 + 1/16 + ... is 1, by Step 2. Which part of that logic is giving you trouble? If you can focus on the logic of these steps you will understand the process. You can have private intuitions about "the end" or whatever your intuitions may be, but when doing math, you need to focus on the math itself.

The raw amount is meaningless without knowing the concentration, and the resulting activity per liter. 1.8 g of tritium in a liter of water is quite different than the same amount in 10,000 liters https://www.reuters.com/world/asia-pacific/japan-release-fukushima-water-into-ocean-starting-aug-24-2023-08-22/ “The water will initially be released in smaller portions and with extra checks, with the first discharge totalling 7,800 cubic metres over about 17 days… That water will contain about 190 becquerels of tritium per litre, below the World Health Organisation drinking water limit of 10,000 becquerels per litre, according to Tepco”

Yes, such batteries exist https://en.m.wikipedia.org/wiki/Betavoltaic_device Separating tritiated water is difficult and might not be cost-effective at low concentrations. If you do mass separation you’ll also get water with O-18, which has the same mass. So there’s probably a threshold below which it’s not worth the effort.

Any point 50 miles south of equator. According to the definition of manifold, it already has necessary structures, specifically, it has neighborhoods defined and, moreover, homeomorphic with Euclidean neighborhoods. It does not necessarily have a metric.

No, we use the partial sums trick to define the sum of an infinite series. As you note, the limit of a sequence is given by the epsilon-N definition. That's the right definition. (ps) The absolute value should be LESS THAN epsilon. Right, the sum of 1/2^n is "obviously" 1. Now if someone says to us, well I don't believe that, how can you make MATH out of it? How can you lay down some basic principles from which the fact that the sum is 1 will follow LOGICALLY? And THAT's what the limit of the partial sums definition is. It's a way of FORMALIZING what we already see must be true. In other words we already know what we want the answer to be. The partial sums are a clever way of constructing a framework in which what we "know" to be true, can be logically proven to be true. Does that help? Are we converging, no pun intended, to understanding? The partial sums are a way of formalizing our intuition. Exactly in the same way that the epsilon-N definition formalized our intuition that the limit of the sequence 1/2, 3/4, 7/8, ... should be 1. We already know what answer we want to get. The epsilon-N definition is a formalization that lets us logically derive the answer we wanted to get in the first place. In a sense, this whole business is an inversion of how people usually see math. People think that in math we have a problem and we want to find the answer. But in many cases, we already know the what the answer should be, and we want to create the math that gives us that answer!

Because that is how they define the sum of an infinite series. We want to define the sum 1/2 + 1/4 + 1/8 + ... But we don't know how to add up infinitely many things. So we DEFINE the sum to be the limit of the sequence of partial sums. The sequence of partial sums is 1/2, 3/4, 7/8, 15/16, ... Can you see that? Ok now the sequence of partial sums happens to have the limit 1. That follows from the definition of the limit of a sequence. Do we perhaps have to review that? That's actually the trickiest part of all this. Once we have that, the rest is easy. The sequence of partial sums has the limit 1. We are not defining 1 differently, it's the same old familiar number 1. We are noting that the limit of the sequence of partial sums is 1. Then, since our goal was to somehow define the infinite sum, we define the sum of the series 1/2 + 1/4 + 1/8 + ... to be whatever the limit of the sequence of partial sums is, which in this case happens to be 1. Is that any more clear? Once we know what the limit of the sequence of partial sums is, we just make an arbitrary rule to define the sum of the series as the limit of the sequence of partial sums. Only in this case it turns out to not really be arbitrary, but actually rather clever ... since we've found a sensible way to define the sum of an infinite series. The reason it's sensible, is that the sum of that series should be 1 if it's anything at all; and now we've found a way to define it logically so that it works out.

It is not wrong. But three bars make it clear that it is a definition rather than an equation.

Yes. The partial sums of 1/2 + 1/4 + 1/8 + ... are 1/2, 3/4, 7/8, ... and the limit of that sequence of partial sums is 1. So the sum of the original series is 1 by definition. Definitions can't be correct or incorrect, only useful or not, insightful or not. The entire point of the formal definition is to bypass meaningless and unanswerable questions involving "the end." There are no answers to those kinds of speculations nor is there really any meaning in them. Instead, we substitute the clever definition that allows us to formally prove that the sum of 1/2^n is 1, and we let everyone have their own private intuitions as long as we agree to use the formalism.

Perhaps it might be clearer if instead of they have said

The notation says that the sum is defined as the limit of the partial sums. It's defined to be 1, the limit of the partial sums. That's actually the clever part of the definition. We can't make sense of "what is the sum after infinitely many operations?" or "Isn't there a tiny little bit left over?" and so forth. The limit definition avoids those problems by providing a precise definition of the sum of an infinite series.

Yes, I should have waited for someone with actual knowledge (i.e. you) to comment on that. While I am aware of Darwinistic influences, it was a long time ago when I read Nietzsche. While his anti-religious stance left a lasting impression (must be around high school/Abitur) I was a bit worried that my memory might conflate bits that should be attributed to his sister (and an overall social-darwinistic view). And I agree, the idea of some sort of salvation or transcendence is very palpable in his writing (again, based on my limited understanding). But here you will need to define what you think an "idea of a Jesus" is. In the Christian religious sense, no. But if you mean Jesus as as stand-in for an enlightened (whatever that may be) person, then perhaps but specifically for Nietzsche the wording might be awkward. One big difference (again, in my mind) beside the organized religion part is that Jesus gathered followers whereas Nietzsche was also preaching to some degree, but focused on individualism. While I agree, that in the parable Nietzsche establishes that without the "sun (i.e. religion)" as a guiding post, there is a need to find an alternative (or else being lost in nihilism). But as such, I semi-disagree that the Uebermensch fills the role of the god. The reasons is that phrasing could imply another sole source of hierarchical morality. Rather, the idea alludes to an human ideal that folks should strive towards. The gap would not be filled by a being, but by humanity. A new village has to be constructed in which the villagers remove themselves from using outdated (and objective) morals but rather define it anew.

Yes you are considering the right things this time. As regards the start point, even simple counting has a start point 1,2,3........ But it has no end point unless you run out of numbers to count., which of course you will not. That is what is meant by infinity in this case. (remember there are other cases) An absolutely spot on answer to the series part of the question. Clear compact and brings out the essential points. +1 I would add to this that for further information @Boltzmannbrain should study Cauchy sequences as this is one good way of dealing with this subject. https://en.wikipedia.org/wiki/Cauchy_sequence

End of 4th paragraph.

The sum is defined as the limit of partial sums. So if we have 1/2 + 1/4 + 1/8 + 1/16 + ..., the partial sums are: 1/2, 3/4, 7/8, 15/16, ... The limit of the sequence of partial sums is 1. So by definition the sum of the original infinite sum is 1. It's explained here on Wiki. https://en.wikipedia.org/wiki/Series_(mathematics) "it is sometimes possible to assign a value to a series, called the sum of the series. This value is the limit as n tends to infinity (if the limit exists) of the finite sums of the n first terms of the series, which are called the nth partial sums of the series."

You will never understand this subject, because its irrational nonsense. All the solutions are nonsense. Einstein's conclusions about warping time and distances and mass, is nonsense. This has been proven beyond doubt. You cant get rational science truth from a nonsense hypothesis. There needs to be an agreement by the majority of scientists that their dogma about Einstein is full of nonsensical claims and that there is most likely aa much better correct interpretation. But dogma belongs to religious belief and that's what Physics of Einstein is based on. Few are interested in truth, they prefer comfortable lies that sound like science fiction. Because that's more exciting. Like Santa and the tooth fairy, exciting but imaginary.