JVNY

Agreed. Consider the Gravitron, the amusement park ride that spins around and subjects riders to 3g force (due to the change of direction from spinning). If that were the same as linear acceleration (speeding up) of 3g's, you would be able to measure relativistic effects on the ride after only a few days of constant spinning.

No objections.

Decraig, this example is quite good, but I don't "feel" the release from the paradox using it. Others might. md65536's explanation based on simultaneity seems the better way. The most fundamental difficulty seems to me to be reconciling symmetry with the outcome of the inertial triplet and the a=1 accelerating triplet in post 391 above. Each is in motion relative to the other, and they meet up again after their first crossing. So a naive application of special relativity would say that each's clock runs slow to the other, and thus at their second meeting each must observe the other's clock to be behind his own -- which is plainly false. It cannot be that each clock runs slower to the other. The accelerating triplet's clock runs slower to the inertial triplet, and the inertial triplet's clock runs faster to the accelerating twin. The two are simply not symmetrical to each other and cannot be -- and it is the supposed symmetry of the two that drives the paradox. It may be better to give up symmetry here and focus on the relativity of simultaneity. Although it would be great if the example resonates with other readers.

Xyzzy, on your question I do not know what you mean by coordinate speed. If you mean the time that it takes for light to travel a straight radial path toward a mass, reflect, then travel a straight radial path back to the source, as measured by an observer at the source, then I agree. That two leg path is slower as measured by an observer at the light source than the same flash takes for the same two legs absent the mass. But then I do not know what you mean by it being unphysical. There is a very important disagreement here: how to transform the events from the illustrated inertial frame to the ships' frame (or each ship's frame, for those who conclude that the accelerating ships do not share a single reference frame). Iggy is not giving preference to a particular frame. The inertial frame is clear (it is illustrated), so all Iggy is doing is the transform to the ships' frame. Iggy and I draw three conclusions. First, that by accelerating each ship inversely to its distance from the front ship one keeps the ships at the same proper distance, that is the same distance in their accelerating reference frame. Each will have a vertical worldline in that frame, always the same distance apart (just as they would if they were in inertial motion with respect to the inertial frame). Second, that all ships agree at all times on their common velocity (just as they would if they were in inertial motion with respect to the inertial frame). Third, that the ships agree on the simultaneity of events in their frame (just as they would if they were in inertial motion with respect to the inertial frame). Xyzt, am I correct in concluding that you agree with the second conclusion (but consider it unimportant), and that you disagree with the first and third?

Here is a good presentation showing how the proper distance stays constant using the inversely proportional acceleration relationship that Iggy refers to. When you Lorentz transform to the ships' frame, they stay 0.25 apart (for the three ships in the second scenario) or 0.5 apart (for the two ships in the first scenario). http://www.csupomona.edu/~ajm/professional/talks/relacc.ppt The whole presentation is useful, but slides 12-15 are the core for our discussion.

On the Shapiro delay, the picture does not show purely radial travel that we are discussing here. Consider instead a mirror orbiting the gravitational mass between that mass and earth. One sends a signal directly toward the mass. The signal travels radially directly toward the mass, then reflects off the mirror and returns to earth on the same radial path. There is no deflection like the curved path under the mass in the picture. There is no change of direction other than the 180 degree reflection. The light will take longer to make that trip than it would absent the mass. There is no curving in space. But there seems to be curvature in spacetime, and some people say that it is due to gravitational time dilation. On the proper distance, by setting the proper accelerations at 2, 1.33, and 1, one ensures that the ships always stay 0.25 apart in their own reference frame. This is explained more fully in http://www.mathpages.com/home/kmath422/kmath422.htm .

Here is part of the Physics FAQ answer on the quotation and point: "In the 1920 book "Relativity: the special and general theory" he wrote: . . . according to the general theory of relativity, the law of the constancy of the velocity of light in vacuo, which constitutes one of the two fundamental assumptions in the special theory of relativity [. . .] cannot claim any unlimited validity. A curvature of rays of light can only take place when the velocity of propagation of light varies with position. Since Einstein talks of velocity (a vector quantity: speed with direction) rather than speed alone, it is not clear that he meant the speed will change, but the reference to special relativity suggests that he did mean so. This interpretation is perfectly valid and makes good physical sense, but a more modern interpretation is that the speed of light is constant in general relativity. The problem here comes from the fact that speed is a coordinate-dependent quantity, and is therefore somewhat ambiguous. To determine speed (distance moved/time taken) you must first choose some standards of distance and time, and different choices can give different answers. This is already true in special relativity: if you measure the speed of light in an accelerating reference frame, the answer will, in general, differ from c." http://math.ucr.edu/home/baez/physics/Relativity/SpeedOfLight/speed_of_light.html So even that careful web site seems to go back and forth on the answer. This is in part why I asked this question here, to get everyone's views.

Yes, the center ship is equidistant from the front and rear ships at the start. All three are at rest in the inertial frame, with rear at x=0.5, center at x=0.75, and front at x=1.0. Then, when they accelerate, they maintain their proper distance in their accelerating frame. In their frame, there is always 0.25 distance between rear and center, and 0.25 distance between center and front. In the inertial frame the distances length contract, however. The scenarios relate to the title because it seems that the acceleration pattern causes the rearward flash to return to the center after the forward flash returns to the center in the ships' frame, even though they travel the same spatial distance in the ships' frame. Analogize to gravity, and the same would occur. This seems to be the first step in a deeper analysis that may well end with your result -- that light is still traveling at c, but there is a spacetime effect that explains why the rearward or downward flash returns later.

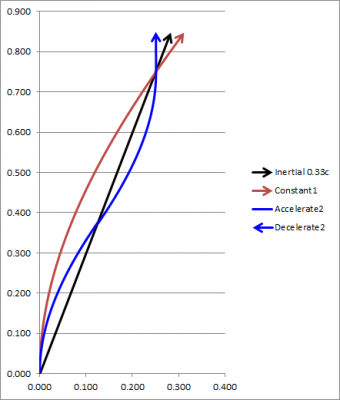
Perhaps members can comment on the following diagram of triplets, whether the calculations are correct, and if it makes sense then how it relates to their explanation of the paradox. Two triplets are at rest at the origin of the inertial frame in the Minkowski diagram. The third triplet is traveling inertially with respect to the inertial frame at 1/3c. When the third triplet reaches the origin, all three agree on simultaneity because they are at the same point. They set their clocks at zero. Simultaneously, the first triplet begins constant acceleration at 1 light year per year^2, and the second triplet initiates a pattern of acceleration at 2 LY per Y^2 for 0.125 LY in the inertial reference frame, then deceleration at the same rate for the same distance. The result is that all three meet again in the inertial frame at (0.25 LY, 0.75 Y). They agree on simultaneity because they are at the same point, and they compare clocks. What results? The first triplet's clock reads 0.693 LY. One can calculate this by the formulas for relativistic travel at a constant acceleration found at: http://math.ucr.edu/home/baez/physics/Relativity/SR/rocket.html. The second triplet's clock reads 0.693 LY. One can calculate proper time for him by the same formulas first for the acceleration leg, then double it for the total (as the website states, you can use the same formula because you are just running the clock backward on the second leg). The third triplet's clock reads 0.707 LY. This is the 0.75 LY in the inertial frame dilated by the Lorentz factor for 1/3c travel (that is, divided by 1.06). Each triplet had the same average speed, 1/3c (0.25 LY / 0.75 Y). However, the accelerating triplets' clocks ran slower than the inertial triplet's clock. The first triplet underwent constant proper acceleration of 1, whereas the second triplet underwent (a) zero net acceleration and (b) constant absolute proper acceleration of 2. Yet their clocks ran at the same rate. I would appreciate it if anyone could confirm or correct the calculations. If the calculations are correct, then average speed is not relevant. The accelerating triplets achieved higher velocity (0.6c according to the formulas at the website above). Time dilation is disproportionately higher at higher velocities, which should explain why the accelerating triplets' clocks ran slower than the inertial triplet's clock. Also, I don't think that the absolute amount of acceleration that one feels is relevant. Here one triplet felt absolute acceleration of 2 over the same distance that the other felt absolute acceleration of 1. Yet their clocks ran at the same rate. I suspect that this is because they traveled at the same speeds for the same times although in different patterns. This seems different from gravity. If a clock experienced gravity of 2 from the left and then 2 from the right, I think that the gravitational time dilation would be greater than that for a clock that experienced gravity of 1 from a single side for the same total time.

Yes and no. I believe that the ships remain at rest with respect to each other, maintain their proper distance, and agree on the simultaneity of events, all in their own single accelerating reference frame. However, their clocks do not run at the same rate. The rear ship's clock runs at 50% of the rate of the front clock, and the center at 75% of the rate of the front clock. This is the equivalence principle in action, just as clocks closer to a gravitational mass run slower than those farther away. The ships can always compensate for this and show the same clock times. The rear ship, for example, can program its clock to record 2 units of time for every 1 unit that elapses at the rear. Then its clock will always show the same time as the front clock (simultaneously in the ships' frame). I think that this is what Iggy means in post 40 when he says "We will have the forward ship be the timekeeper." This does not change the passage of time. Time continues to elapse more slowly the farther back one is from the front. But it does allow the ships to label events that they agree are simultaneous with the same clock time. Here are some links from earlier posts to explanations. For setting up the hyperbolas, see http://en.wikipedia.org/wiki/Rindler_coordinates For details on the locus of simultaneity and drawing the line of simultaneity, see http://mathpages.com/rr/s2-09/2-09.htm

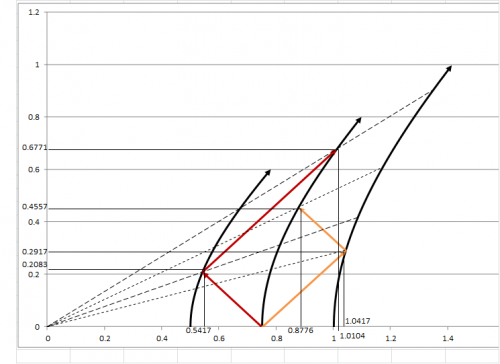
Some of this confusion is due to my having posted two separate scenarios. Apologies. In the first scenario, the front ship sends a flash toward the rear ship, and the rear ship sends a flash toward the front ship. In the second, there is also a center ship. The center ships sends flashes forward and rearward; they reflect off of the front and rear ships, then return to the center ship. The bulk of the discussion thread has covered the first scenario. It seems from the calculations, confirmed by Iggy, that the flash from the front reaches the rear simultaneously (in the ships' frame) with the flash from the rear to the front. So perhaps now let's turn to the second scenario. So here is the scenario and a Minkowski diagram. The three ships start out at rest in the inertial frame, rear at x=0.5, center at x=0.75, and front at x=1.0. Simultaneously, center sends flashes rearward and forward, and the ships begin constant proper acceleration of rear a=2, center a=1.33, and front a=1. This maintains their proper distance in their own accelerating reference frame. When a flash hits a ship, it reflects and returns to the center ship. The results, which are based again on the relativistic rocket formulas from Dr. Baez's website, are as follows. In the inertial frame, the order of light flashes striking ships is: rearward flash hits rear ship, then forward flash hits front ship, then forward flash returns to center ship, then rearward flash returns to center ship. The diagram shows the inertial frame times and locations for each strike. In the ships' frame, the order is different, as you can see from the lines of simultaneity. The forward flash hits the front ship first, then the rearward flash hits the rear ship, then the forward flash returns to the center, and finally the rearward flash returns to the center. In their proper times (not shown on the diagram), the rearward flash hits the rear at rear ship time Tr=0.203; the forward flash hits the front ship at front ship time Tf=0.288; the forward flash returns to the center at center ship time Tc=0.432, and finally the rearward flash returns to the center at center ship time Tc=0.608. This seems consistent with radial light travel and the Shapiro delay, if one sends signals in opposite directions, one toward the gravitational mass, and one away from it.

OK, thanks.

I posited two ships, front and rear, separated by 0.5. It works just the same for a single ship as you posit. Then one would posit a single ship of proper length 0.5. The front accelerates at a=1 and sends a flash to the rear, simultaneous with the rear accelerating at a=2 (and all points in between accelerating between 1 and 2 such that the whole ship maintains its proper length of 0.5). In that case, in inertial frame time t=0.375 the flash from the front of the ship travels 0.375 to the left. The rear of the ship travels 0.125 to the right, and the flash strikes the rear of the ship. Are we in agreement on that?

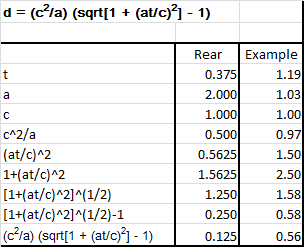
OK, so let's start with the rear ship, and an example from Dr. Baez's website http://math.ucr.edu/home/baez/physics/Relativity/SR/rocket.html. With the rear ship, we use c=1, a=2 and t=0.375. Then you just plug c, a and t into the formula for d from Dr. Baez's website. The result is distance traveled for the rear ship of 0.125 to the right. In t=0.375, the rearward flash travels a distance of 0.375 to the left. Combined, that is 0.125 + 0.375 = 0.5, and the flash has closed the 0.5 distance between the ships in the ground frame. Then do the same with c=1, a=1.03 (the equivalent of 1g, per that website), and t=1.19. The result is distance traveled of 0.56, which is what the website gives in the first example of typical results for a=1g travel (excerpted here): These equations are valid in any consistent system of units such as seconds for time, metres for distance, metres per second for speeds and metres per second squared for accelerations. In these units c = 3 × 108 m/s (approx). To do some example calculations it is easier to use units of years for time and light years for distance. Then c = 1 lyr/yr and g = 1.03 lyr/yr2. Here are some typical answers for a = 1g. T t d v γ 1 year 1.19 yrs 0.56 lyrs 0.77c 1.58 Here is a chart showing the two results from the formula, d=0.125 in the case of the rear ship, and d=0.56 in the website example:

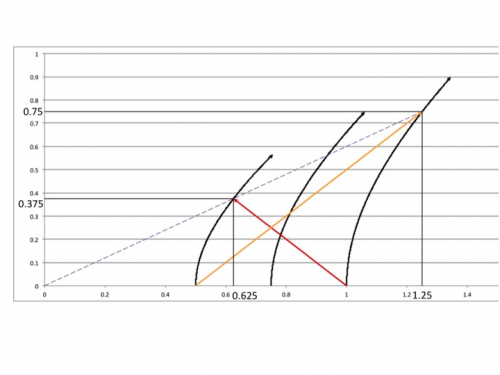
Here are the formulas, from http://math.ucr.edu/home/baez/physics/Relativity/SR/rocket.html Inertial frame time: t = sqrt[(d/c)2 + 2d/a] eq. 1 Inertial frame distance traveled: d = (c2/a) (sqrt[1 + (at/c)2] - 1) eq. 2 Ship's elapsed proper time: T = (c/a) ch-1 [ad/c2 + 1] eq. 3 Inertial frame velocity: v = at / sqrt[1 + (at/c)2] eq. 4 Each flash must close 0.5 distance in the inertial frame. The rearward flash closes with the rear ship (which accelerates at a=2), and the flash travels one unit of d for every unit of t (because c=1), so the flash strikes the rear ship when d + t = 0.5. d + t = 0.5 Using equations 1 and 2 above: (c2/a) (sqrt[1 + (at/c)2] - 1) + sqrt[(d/c)2 + 2d/a] = 0.5 Solving that equation, t = 0.375 and d = 0.125 Solving eq. 3 above using a = 2, t = 0.375 and d = 0.125, yields T = 0.346. The forward flash must cover 0.5 distance plus the distance that the front ship travels, so that the flash strikes the front ship at t = 0.5 + d, or t - d = 0.5. Using equations 1 and 2 above, where a = 1 for the front ship, sqrt[(d/c)2 + 2d/a] - (c2/a) (sqrt[1 + (at/c)2] - 1) = 0.5 Solving that equation, t = 0.75 and d = 0.25 Solving eq. 3 above using a = 1, t = 0.75 and d = 0.25, yields T = 0.693 These are simultaneous in the ships' frame because each is at rest with respect to the other. Their velocities are equal, 0.6c, determined using eq. 4 above for each ship. Another way to confirm that the two ships agree on simultaneity is to determine the line of simultaneity, the dashed line in the diagram, which has the slope 0.6. One determines the locus of the line as follows. If a point undergoes "constant proper acceleration a0," then the "locus of simultaneity constantly passes through the point (-1/a0, 0), and it maintains a constant absolute spacelike distance of -1/a0 from that point." See http://mathpages.com/rr/s2-09/2-09.htm. For the rear ship, that means that the locus of simultaneity is (-1/2, 0), or (-0.5, 0). Since the rear ship begins at 0.5, that means that its locus of simultaneity is at (0.5 - 0.5, 0), that is (0, 0). For the rear ship, the locus of simultaneity is (-1/1, 0), or (-1, 0). The front ship starts at 1.0, so its locus of simultaneity is (1.0 - 1.0, 0), that is (0, 0). Therefore the dashed line of simultaneity starts at (0, 0), and with a slope of 0.6 crosses the rear and front world lines as the flashes strike each.

OK, here are the calculations of the proper times for the ships. The rearward flash hits the rear ship at rear ship's proper time 0.346, and front ship's proper time 0.693. The forward flash hits the front ship at the rear ship's proper time 0.346, and the front ship's proper time 0.693. So the flashes arrive simultaneously in the ships' frame. Riders on each ship agree that the flashes arrive simultaneously, even though they disagree on what time the flashes arrived. The rear clock runs slower than the front clock in the ships' own frame (the rear at half the rate of the front), so although they agree on simultaneity, if they set their clocks at zero upon initiating acceleration then a rider on the rear will say that the flashes arrived at time 0.346, whereas the rider on the front will say that the flashes arrived at time 0.693.

OK, let's stay away from the issue of light speed, and just focus on simultaneity of events. Clearly in the lab frame the flash from the front strikes the rear (at lab time t=0.375) before the flash from the rear strikes the front (at lab time t=0.75). Based on the hyperbola formulas and the diagram above, is it the case that in the ships' reference frame the rearward flash arrives at the rear ship simultaneously with the forward flash arriving at the front ship (along the dashed line of ship frame simultaneity)?

I am starting to work through the materials. Start with xyzt's question of whether the end to end flashes arrive simultaneously in the accelerating frame, using hyperbolic formulas. Using the formulas, I believe that yes the flashes arrive simultaneously in the accelerating frame. Consider two ships, rear and front, at rest in the inertial lab frame, rear at x=0.5 and front at x=1.0. Simultaneously each flashes a light at the other ship and begins to accelerate so as to maintain their proper distance, rear at proper rate a=2, front at proper rate a=1 (all measures unitless, so c=1, the y axis can be for example years, the x axis light years, and acceleration light years per year^2). Below is a Minkowski diagram from the lab frame, which shows that the flashes strike simultaneously in the ships' frame. The dashed line marks simultaneity in the ships' frame (each ship's velocity is 0.6c there when the flashes strike). The diagram also shows for reference the mid point between the ships, which also maintains proper distance (proper rate a=1.33). The light flashes cross to the left of center, but nonetheless reach the ships simultaneously. Perhaps there is common ground between Iggy and xyzt. It seems that there are two ways to measure speed. One is what Iggy refers to, and xyzt calls coordinate speed. The diagram illustrates that kind of speed -- light goes faster (in both directions) when it is traveling in the area to the right, and it goes slower (in both directions) when it is traveling in the area to the left. This is consistent with the Shapiro delay. The other is the speed that someone measures locally, which is always c. Sorry, the post did not take the diagram. Here it is as an attachment.

Thanks to all for the answers. I will follow the suggestions to read the various references, because I seem to have gotten in a bit over my head here.

OK, thanks.

Yes, that is clearly the case in the lab frame. Say the elevator is at rest in the lab frame. Simultaneously (in both elevator and lab frame) there are two flashes, one up form the floor and one down from the ceiling, and the elevator begins to accelerate upward. The two flashes cross below the middle point of the elevator in the lab frame for the reasons you describe. Since they are at the same place when they cross, simultaneity is not relative there: they also cross below the middle in the elevator frame. However, the results are not symmetrical for the ultimate events of the flashes striking the floor and the ceiling. These two events are separated in space, so simultaneity is relative. In the ground frame, the downward flash strikes the floor first. In the elevator frame the two flashes strike the floor and the ceiling simultaneously. This is from the first Minkowski diagram attached to the first post. I am focused on what happens in the elevator frame, because that is the frame that Einstein uses as the one that is equivalent to being in gravity. Does that make sense?

On second thought, it works well for light going up the gravity well. But it does not explain why light also goes more slowly when it travels down the gravity well. The Minkowski diagrams attached to the first posting show that light also travels more slowly going rearward (down the well), not just forward (up the well). What explains this (expressed conceptually or visually)? In the first diagram, for example, it takes the same time for a flash to go rearward as forward (by the fact that the two flashes start simultaneously in the ships' frame from each end, and strike the opposite ends simultaneously in the ships' frame). In the second diagram, the flash from the center to the rear takes the same amount of center ship proper time as the flash takes to return from the rear to the center. I did not include these proper times in the diagram, but you can run the numbers and confirm that the rearward flash hits the rear ship when the center ship's clock reads T=0.3041. After reflecting off the rear ship, the flash strikes the center ship when the center's clock reads T=0.6082. It seems that travel in either radial direction is slower. This seems to be borne out by the Shapiro experiments -- when you break the signal's trip down into component segments, there is a segment toward the sun and a segment away from the sun, and light travels slower on both of these legs. Following the approach you suggest, the photos should gain energy on the first leg (going toward the sun), which would counteract the loss of energy going away from the sun, leaving the only net effect being the non-radial travel as the signal curves around the sun.

That works, thanks.

It does mathematically, but I was hoping for something conceptual (even visual). For example, it seems obvious that a light flash will have lower velocity traveling from 12 o'clock on a clock face to 6 o'clock if it gets bent around by gravity and has to travel around the rim of the face. It does not travel at c measured as net distance traveled divided by time, because it travels a greater total distance (the distance along the curve). But how does one conceptualize the light flash going slower than c when it travels radially directly from 12 o'clock to the center of the face, then back again? Or, say, from 12 o'clock straight along the diameter to 6 o'clock? One way to think of it is to turn the clock face 90 degrees so that you look directly at the rim, then position yourself to look directly at 3 o'clock, then observe the end of the second hand as it travels from 12 o'clock to 6 o'clock. You will effectively be looking at the second hand traveling in only one dimension (a rightward line from 12 o'clock on your left to 6 o'clock on your right -- assume that your vision is not good enough to see the depth involved). In that case, the second hand will travel to your right more slowly the closer it is to 12 and 6 o'clock (because it will be traveling mostly toward or away from you, even though you cannot really see that). It will travel faster around 3 o'clock (because there is very little curvature there, so it is mostly traveling to your right, with very little travel toward or away from you). Is that the sort of thing that happens in spacetime with a radial light path? That seems to put everything in space terms, not in time terms, so it is probably not right as a description of spacetime. Elsewhere (in discussions of Shapiro delay), authors say that the effect in the direction toward or away from the gravitational mass is the result of gravitational time dilation, which suggests that the second hand analogy is wrong.

Thanks. XYZT, is there any way that you can explain why this slowing down occurs in a way that will resonate with someone who is only so far studying special relativity? The assumption is that the light moves directly down the gravity well, reflects off of something there, and then returns directly up the gravity well (I suspect that this is what you call "radial" in both directions). Various sources say that it is a result of gravity contracting rulers and dilating clocks near the mass; or curving of space, or curving of space and time. Yet there should be no curving of the light's path like the famous experiments viewing stars during a solar eclipse, because the path is straight down then straight back up; and still the slowing occurs for the distant observer. I am hoping for an Einstein explanation to a five year old