Mordred

That's definitely a view I share, in my 36 years of studying particle physics including my degree. One learns that a particle is not some corpuscular solid. The pointlike attributes can be described by the De Broglie and Compton wavelength. Good article above its one Of commonly refer to, if you focus your learning upon the above understanding you will get a solid grasp. I have often stated "solid is an illusion". Funny part was when I first started learning particle physics I was a strong particle vs waveform advocate.

Not sure I would want to be close enough to see a supernova except through a strong telescope.

I'm curious as to why you keep trying to visualize an atom with some form of sentient life. ? No particle thinks... it cannot know anything The mass term of every particle is due to its coupling strength to their respective fields that the particle interacts with. Mass is defined as resistance to inertia change. There are no ropes involved so the above makes no sense. As others have already mentioned there are forces involved and each force has a ratio of change due to distance.

Atoms don't think or read indicators. They simply respond to their respective fields through attraction and repulsion interactions.

So we know the total resistance to inertia change.

Though particle physics uses GR GR itself only plots the worldline paths of particle momentum. Which is why I always get a kick out of people discounting GR because it didn't predict dark matter or dark energy. It's not the function of GR to predict the particle model only how particles move in spacetime.

Any integer spin either 1 or zero as most bosons are spin 1 with the exception of Higgs and possibly graviton spin 2 assuming gravitons exist.

The Dirac sea was originally developed when there were only two known particles. The electron and the proton. The negative energy states which make up the sea were filled with the positive energy states. However the theory didn't consider spin zero particles ie bosons which you can have any number of bosons of the same state in the same space. This in itself meant there is no limit of bosons that could fill a hole. Some bosons such as the photon are it's own antiparticle as it is charge neutral. It was the problem of bosons and advent of QFT that made the Dirac sea or hole theory problematic and essentially became useless. In essence you could have an infinite number of bosons in every hole.

No you have one too many humps the false and true vacuum will have their own minima with the minima of the false vacuum higher than the true vacuum. The tunneling must occur from the false vacuum to true vacuum. Through the potential barrier between them. See image on this link https://en.m.wikipedia.org/wiki/False_vacuum Here is an older paper of false vacuum. It was widely in inflationary cosmology. Allen Guth first applied it to inflation however Coleman was also using false vacuum at roughly the same time period. https://www.google.com/url?sa=t&source=web&rct=j&url=http://www.physics.princeton.edu/~steinh/ph564/Coleman.pdf&ved=2ahUKEwiu7ev1n9nmAhU0HjQIHWVKD1kQFjALegQICBAB&usg=AOvVaw2C_EEYqv4zbu9jrXvoXGk1 This is an older application however it points out all the essential details.

This article has a list. https://www.google.com/url?sa=t&source=web&rct=j&url=https://cds.cern.ch/record/534658/files/0201198.pdf&ved=2ahUKEwjP9vHV59jmAhVQ_J4KHUd_DhIQFjABegQIAxAB&usg=AOvVaw1mim8GrdtR9YRkL-Jxf402 Though you would need to go through the CKMS and PMNS mixing angles via the unitary triangle mentioned in the above article for the mass mixing angles for each particle species in each generation. False vacuum is a higher state than the true vacuum. You will also need to ensure their is a potential barrier between the two for quantum tunnelling from the false vacuum to the true vacuum.

The Higgs vacuum expectation value is 246 Gev. It is always a non zero value. One has to be careful on how one defines a true vacuum. For example a true vacuum could mean the Einstein Vacuum which is devoid of all particles. However with zero point energy there is always quantum fluctuations leading to particle production. Every coupling constant is defined by its own function. This is true for the SM coupling constants as well as those in Supersymmetry models.

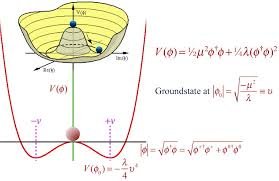
The Higgs Mexican hat potential does not below it's vacuum expectation value. Not all coupling constants obey the same relations to other coupling constants they each have their own potential curves. In essence any equation that describes your potential graph will not match the one I posted.

Be careful of such bold statements for example try to define that statement above to the Higgs coupling constants. First ask yourself the function of a coupling constant in regards to mass. (Hint). Mass is resistance to inertia change. (Second hint) You might also want to better understand Langrangian and the principle of least action with the above. https://www.feynmanlectures.caltech.edu/II_19.html QFT is based on perturbation theory which employs action in accordance to that principle. Here this will help call it the QFT preliminary Ie chapter 1. QFT can be described as a coupling of SR and QM in the non relativistic regime. 1) Field :A field is a collection of values assigned to geometric coordinates. Those values can be of any nature and does not count as a substance or medium. 2) As we are dealing with QM we need the simple quantum harmonic oscillator 3) Particle: A field excitation Simple Harmonic Oscillator [math]\hat{H}=\hbar w(\hat{a}^\dagger\hat{a}+\frac{1}{2})[/math] the [math]\hat{a}^\dagger[/math] is the creation operator with [math]\hat{a}[/math] being the destruction operator. [math]\hat{H}[/math] is the Hamiltonian operator. The hat accent over each symbol identifies an operator. This formula is of key note as it is applicable to particle creation and annihilation. [math]\hbar[/math] is the Planck constant (also referred to as a quanta of action) more detail later. Heisenberg Uncertainty principle [math]\Delta\hat{x}\Delta\hat{p}\ge\frac{\hbar}{2}[/math] [math]\hat{x}[/math] is the position operator, [math]\hat{p}[/math] is the momentum operator. Their is also uncertainty between energy and time given by [math]\Delta E\Delta t\ge\frac{\hbar}{2}[/math] please note in the non relativistic regime time is a parameter not an operator. Physical observable's are operators. in order to be a physical observable you require a minima of a quanta of action defined by [math] E=\hbar w[/math] Another key detail from QM is the commutation relations [math][\hat{x}\hat{p}]=\hat{x}\hat{p}-\hat{p}\hat{x}=i\hbar[/math] Now in QM we are taught that the symbols [math]\varphi,\psi[/math] are wave-functions however in QFT we use these symbols to denote fields. Fields can create and destroy particles. As such we effectively upgrade these fields to the status of operators. Which must satisfy the commutation relations [math][\hat{x}\hat{p}]\rightarrow[\hat{\psi}(x,t),\hat{\pi}(y,t)]=i\hbar\delta(x-y)[/math] [math]\hat{\pi}(y,t)[/math] is another type of field that plays the role of momentum where x and y are two points in space. The above introduces the notion of causality. If two fields are spatially separated they cannot affect one another. Now with fields promoted to operators one wiill wonder what happen to the normal operators of QM. In QM position [math]\hat{x}[/math] is an operator with time as a parameter. However in QFT we demote position to a parameter. Momentum remains an operator. In QFT we often use lessons from classical mechanics to deal with fields in particular the Langrangian [math]L=T-V[/math] The Langrangian is important as it leaves the symmetries such as rotation invariant (same for all observers). The classical path taken by a particle is one that minimizes the action [math]S=\int Ldt[/math] the range of a force is dictated by the mass of the guage boson (force mediator) [math]\Delta E=mc^2[/math] along with the uncertainty principle to determine how long the particle can exist [math]\Delta t=\frac{\hbar}{\Delta E}=\frac{\hbar}{m_oc^2}[/math] please note we are using the rest mass (invariant mass) with c being the speed limit [math] velocity=\frac{distance}{time}\Rightarrow\Delta{x}=c\Delta t=\frac{c\hbar}{mc^2}=\frac{\hbar}{mc^2}[/math] from this relation one can see that if the invariant mass (rest mass) m=0 the range of the particle is infinite. Prime example gauge photons for the electromagnetic force. Lets return to [math]L=T-V[/math] where T is the kinetic energy of the particle moving though a potential V using just one dimension x. In the Euler-Langrange we get the following [math]\frac{d}{dt}\frac{\partial L}{\partial\dot{x}}-\frac{\partial L}{\partial x}=0[/math] the dot is differentiating time. Consider a particle of mass m with kinetic energy [math]T=\frac{1}{2}m\dot{x}^2[/math] traveling in one dimension x through potential [math]V(x)[/math] Step 1) Begin by writing down the Langrangian [math]L=\frac{1}{2}m\dot{x}^2-V{x}[/math] next is a derivative of L with respect to [math]\dot{x}[/math] we treat this as an independent variable for example [math]\frac{\partial}{\partial\dot{x}}(\dot{x})^2=2\dot{x}[/math] and [math]\frac{\partial}{\partial\dot{x}}V{x}=0[/math] applying this we get step 2) [math]\frac{\partial L}{\partial\dot{x}}=\frac{\partial}{\partial\dot{x}}[\frac{1}{2}m\dot{x}^2]=m\dot{x}[/math] which is just mass times velocity. (momentum term) step 3) derive the time derivative of this momentum term. [math]\frac{d}{dt}\frac{\partial L}{\partial\dot{x}}=\frac{d}{dt}m\dot{x}=\dot{m}\dot{x}+m\ddot{x}=m\ddot{x}[/math] we have mass times acceleration Step 4) Now differentiate L with respect to x [math]\frac{\partial L}{\partial x}[\frac{1}{2}m\dot{x}^2]-V(x)=-\frac{\partial V}{\partial x}[/math] Step 5) write the equation to describe the dynamical behavior of our system. [math]\frac{d}{dt}(\frac{\partial L}{\partial\dot{x}}-\frac{\partial L}{\partial x}=0[/math][math]\Rightarrow\frac{d}{dt}[/math][math](\frac{\partial L}{\partial\dot{x}})[/math][math]=\frac{\partial L}{\partial x}\Rightarrow m\ddot{x}=-\frac{\partial V}{\partial x}[/math] recall from classical physics [math]F=-\nabla V[/math] in 1 dimension this becomes [math]F=-\frac{\partial V}{\partial x}[/math] therefore [math]\frac{\partial L}{\partial x}=-\frac{\partial V}{\partial x}=F[/math] we have [math]m\ddot{x}-\frac{\partial V}{\partial x}=F[/math]

There is 18 coupling constants in total for the weak, strong and Electromagnetic force including the two Higgs coupling constants but yes we examine all four of the above in that thread. GR gauge group would best be described as the Poincare group SO (3.1) Last I recall supersymmetry had roughly 114 coupling constants lol.

The gauge groups I mentioned are not specifically the harmonic oscillator. QFT accounts for the quantum harmonic oscillator in its gauge groups but that isn't the full story. https://www.google.com/url?sa=t&source=web&rct=j&url=https://www.hep.phy.cam.ac.uk/~gripaios/gft_lecture_notes.pdf&ved=2ahUKEwi79v_N09TmAhVuHzQIHbErDekQFjAAegQIBhAB&usg=AOvVaw2Tq7K0egwVnGx8aslG3PJE Here is a primer QFT takes a considerable time to learn. https://www.google.com/url?sa=t&source=web&rct=j&url=http://www.damtp.cam.ac.uk/user/tong/qft/qft.pdf&ved=2ahUKEwjw6qeL1tTmAhVXs54KHaCABBkQFjAAegQIBRAB&usg=AOvVaw0XQ8pIIPzIxiwafEUsja8F In order to be observed there must be a quanta of action. The external lines on those Feymann diagrams are observable's. (Operators) The internal lines (propogators ) (often thought of as virtual particles) are not observable. Here is the standard model of particle physics (not including Higgs) that is in another post [math]\mathcal{G}=SU(3)_c\otimes SU(2)_L\otimes U(1)_Y[/math] Color, weak isospin, abelion Hypercharge groups. Couplings in sequence [math]g_s, g, \acute{g}[/math] [math]\mathcal{L}_{gauge}=-\frac{1}{2}Tr{G^{\mu\nu}G_{\mu\nu}}-\frac{1}{2}Tr {W^{\mu\nu}W_{\mu\nu}}-\frac{1}{4}B^{\mu\nu}B_{\mu\nu}[/math] Field strengths in sequence in last G W B tensors for SU(3),SU(2) and U(1) Leads to covariant derivative [math]D_\mu=\partial_\mu+ig_s\frac{\lambda_i}{2}G^i_\mu+ig\frac{\sigma_i}{2}W^i_\mu+igQ_YB_\mu[/math] Corresponds to [math]G_{\mu\nu}=-\frac{i}{g_s}[D_\mu,D_\nu][/math] [math]W_-\frac{I}{g}[D_{\mu}D_{\nu}][/math] [math]B_{\mu\nu}-\frac{I}{\acute{g}}[D_\mu,D_\nu][/math] You can find the Higgs on page two https://www.scienceforums.net/topic/117992-the-lagrangian-equation/ In essence we were trying to validate and reverse engineer the equation in post 1. In order to do that I had to examine each gauge group of the standard model. Given by [math]\mathcal{G}=SU(3)_c\otimes SU(2)_L\otimes U(1)_Y[/math]

That theory lost popularity among the scientific community long ago. In essence symmetry gauge theory covers all the aspects of the above without specifying a single particle at all spacetime locations. Now under QFT the particle number density varies accordingly to the field strength.

Merry Christmas everyone everyone

No the mass distribution is homogeneous and isotropic. Homogeneous is no preferred location and isotropic is no preferred direction. In essence the distribution is uniform when both the above is involved However one must look on scales roughly 100 Mpc. This will even out the large scale clusters such as galaxies etc. (Averages to the above). Those temperature differences you see on that map is only 1/1000's of a degree difference. In essence incredibly uniform. The image would correlate early LSS such as galaxy cluster filaments in early development.

Cooler indicates less dense. A higher density would be hotter. Hence at time of CMB the mean average temperature was roughly 3000 CMB. Temperature drops on the inverse of the scale factor a.

Correct for QM, for QFT the Klien Gordon. +1 for studyi

Yes that link refers to quantum decoherence. Little hint anytime you see a reference to creation or annihilation operators your either dealing with QM or QFT. You may find it handy to look up the Bra and ket notations (Dirac notation) To get a better grasp of the mathematics on that link.

The point is the observable universe portion as you extrapolate expansion backwards. It is the region of shared causality with our current observable universe. In the case of an infinite universe each region of shared causality would extrapolate to different points.

Correction to the above gamma is as per GR not gamma matrix. Misread it.

Lol welcome to tensors, gamma in the above is the gamma matrixes. Those are used with the Dirac and Wheyl spinors. Here is decoherence make sure you look at quantum coherence hyperlink. I will have more time later to help

Here this article will help with Wicks rotation. https://www.google.com/url?sa=t&source=web&rct=j&url=https://cds.cern.ch/record/536859/files/0202018.pdf&ved=2ahUKEwicjZX258vmAhV9IDQIHVBBDK4QFjAEegQIBhAB&usg=AOvVaw0pRhVoMpCuLopChA28_OuC I will have time to look at your other questions after work.