-
Posts
10078 -
Joined
-
Last visited
-
Days Won
37
Content Type
Profiles
Forums
Events
Everything posted by Mordred
-
its not as simple a matter as mere calculations in order to renormalize gravity you must eliminate any divergence. a common method used is via a regulator operator. However with gravity we do not know any upper bound ( ultraviolet boundary). Good example being the singularity of a BH.
-
Deuterium BBN reference https://www.astro.uvic.ca/~jwillis/teaching/astr405/astr405_lecture4.pdf equation 18 \[\frac{\mathcal{n}_D}{\mathcal{n}_p\mathcal{n}_n}=6(\frac{m_nk\tau}{\pi\hbar^2})^{-3/2}exp(\frac{Q_D}{k\tau}\]
-
Bump, still examining this still trying to figure out thermal equilibrium dropout of several other particles and relevant atoms via Saha equations
-
It all depends on the mass of the BH. It isn't reliant on the gradient. I'm well aware your not strong on the mathematics so I won't try to post the ZAMO mathematics (zero angular momentum observer) with regards to frame dragging. The details of such can be found here https://www.roma1.infn.it/teongrav/onde19_20/kerr.pdf
-
attending a school is the best way short of that one an work through numerous textbooks choose ones with practice problems.
-

On the Observational constrains of shrinking matter theories
Mordred replied to caracal's topic in Speculations
Careful the overdot on the scale factor is a time derivative for velocity. Will look over the rest later on. Here https://en.m.wikipedia.org/wiki/Time_derivative I don't believe your intention is to modify the fluid equations above The fluid equations directly derive from the thermodynamic laws via the effective equations of state (cosmology). I'm not clear on this statement of yours \[a_{obs0} = a_{real0} = a_{apparent0} = 1\] the scale factor is simply a constant of proportionality as I'm sure your aware the scale factor today is set at 1. the scale factor at some point in the past is simply the ratio of radius of the observable universe then as opposed to today. For example a scale factor of 0.5 the radius of the observable universe would be half what it is today. So I do not know where your getting the extra scale factor terms such as apparent. Nor the need to normalize the above terms as that would remove the usefulness. However the equations above wouldn't work. As I mentioned the overdot is the velocity term of the scale factor in the equation above. If your goal is to match observational data you will also need the full Friedmann equation with the cosmological term. You will still have nonlinearity in point of detail until the Lambda dominant era the universe expansion was slowing down until the Lambda term became dominant a close examination of this will show this occurs roughly at the universe age of 7 Gyrs. The value will vary according the the cosmological parameter dataset used. Via the lookback time equation you have above which is similar enough to the one I posted earlier. None of this still addresses numerous other problems such as the nucleosynthesis, electroweak symmetry breaking, which both rely on thermal equilibrium relations and expansion not to mention the fine structure constant and other related coupling constants which have relations involving radius for their effective strength. Nor have you mentioned any particular cause for shrinking matter and how the rates of the shrinking will correspond to a varying rate of change in expansion rates. The rates of shrinkage would have to correspondently shrink. I fail to think of any viable mechanism as to how that could possibly work. That includes via gravity or any of the fundamental forces. However my feelings as to your model viability is secondary. The point of detail is that you are making the effort to properly model and in that regard I will still assist as one learns from correctly modelling even when the model is wrong. LOL truth be told a good theorist physicist will do everything in their power to prove their own models wrong. That's how they become robust to begin with. One other thing to keep in mind. Even if you fully get the mathematics to work and match the curves I mentioned (they correspond to actual datasets otherwise the theory wouldn't be viable to begin with). You will still need to figure out the cause of shrinkage and what controls that states behavior over time. As well as the cause of its history of variations. That will also need to be mathematically modelled. -

On the Observational constrains of shrinking matter theories
Mordred replied to caracal's topic in Speculations
I would like you to consider the following in terms of Luminosity distance. You can see from the equations above in my previous post that the evolution of matter, radiation and Lambda has significance in distance measurements as well as expansion rates. Furthermore the common formulas you often see for redshift, luminosity, universe age etc do not include those details. example above. here is how luminosity distance relates with the evolution of the above. the energy flux being the measured energy per unit time per unit area of the detector. the luminosity distance is then defined on the radius of the sphere centered on the source in which the absolute luminosity would give the observed flux. \[\mathcal{F}=\frac{\mathcal{L}}{4\pi d^2_L}\] as light travels on null geodesic ds^2=0 \[ds^2=dt^2-at^2[\frac{dr^2}{1-k r^2}+r^2(d\theta^2+sin^2\theta d\phi^2)]\] with k=0 and the various contributions above this gives \[\frac{dr}{1+a_o^2H_o^2 r^2\Omega_k}=\frac{1}{a_o^2H_o^2}\frac{dz}{(1+dz)^2(1+dz\Omega_M)-z(2+z)\Omega_\Lambda}\] which determines the coordinate distance (not proper distance) as a function of redshift for \[r=r(z,H_0,\Omega+M\Omega_\Lambda)\] energy becomes \[E_O=\frac{E}{1+z}\] rate of photon arrival will be time delayed via \[dt_o=(1+z)dt\] \[\mathcal{F}=\frac{\mathcal{L}}{4\pi a^2_Or^2(z)}=\frac{\mathcal{L}}{4\pi d^2_L}\] gives luminosity distance as a function of redshift \[H_O d_L=(1+z)|\Omega_k|^{-1/2}sinn[|\Omega_k|^{-1/2}\int^z_0\frac{d\acute{z}}{\sqrt{(1+\acute{z}^2)(1+\acute{z}\Omega_M)-\acute{z}(2+\acute{z})\Omega_\Lambda}}]\] where sinn(x)=x k=o,sin(x) if k=1, sinh(x) if k=_1 leads to \[H_Od_L=z+\frac{1}{2}(1-\frac{\Omega_M}{2}+\Omega_\Lambda)z^2+\mathcal{O}(z^3)\] where H evolves as \[H_z=H_o\sqrt{\Omega_m(1+z)^3+\Omega_{rad}(1+z)^4+\Omega_{\Lambda}}\] temperature as a function of redshift gives \[T=T_O(1+z)\] the above is a methodology by Juan Garcıa-Bellido in his numerous papers, though you can find similar solutions in Bunn and Hoggs (distance measures) and Lineweaver and Davies. Here is the Hogg paper Distance measures in cosmology https://arxiv.org/pdf/astro-ph/9905116.pdf in this paper you can see similar a similar treatment using E(z) equation 14. The paper further covers angular diameter distance which further relates to luminosity distance. One of the details you should note in the last paper is that many of these factors do not have identical rates of change. see the graphs in the paper above for an example. Those should further highlight the non linearity logarithmic rates of change. -
I have a very simple policy. When I see a posting that the author cannot be bothered to ensure its legible and easy to read. Then I cannot be bothered with that posting. I am positive numerous other readers feel the same way.
-

Acoustic Waves in Air with Variable Sonic Velocity
Mordred replied to sethoflagos's topic in Speculations
I have read numerous Cambridge materials as well. Some of the better examples of various math treatments in numerous fields such as the ones you mentioned and others are contained within them. I have always found them handy -

Acoustic Waves in Air with Variable Sonic Velocity
Mordred replied to sethoflagos's topic in Speculations
Thanks for the info as I tend to collect good literature I may pick up a copy -
The cosmological contribution is a kinetic energy term if you take the critical density term. When you solve the critical density formula you will find it will give an answer that will be approximately 10^{-10} joules/cubic metre. much like photons can power a solar sail even though photons have no inavariant mass the photon has momentum.
-

On the Observational constrains of shrinking matter theories
Mordred replied to caracal's topic in Speculations
Thank you for clarifying that L is a dimensional less parameter, your age calculations are off. Unfortunately the calculations involve the density of matter, radiation, Lambda as well as the curvature term K. You also have to factor in how each expansion contributor evolves over time. the generic formula for the age of the universe is as follows (will vary depending on the applied cosmological parameters.) \[dt=\frac{da}{aH_o}\frac{1}{[\Omega_r(\frac{a_o}{a})^4 \Omega_m(\frac{a_o}{a})^3 \Omega_k(\frac{a_o}{a})^2 \Omega_\Lambda(\frac{a_o}{a})]^2}\] for our universe with K=0 and being Lambda dominant today this simplifies to \[t_o=\frac{2}{3}\frac{1}{H_O}\sqrt{\Omega_\Lambda}\sinh^{-1}\sqrt{\frac{\Omega_\Lambda}{1-\Omega_\Lambda}(\frac{a}{a^3})^3}\] How to determine the decoupling time for the CMB is a lengthy process involving the Saha equation however for out universe without going into all the required decoupling chains etc the solution simplifies to \[t_{dec}=\frac{2}{3H_O (1+z_{dec})^{3/2}}\] quite frankly the only way to truly test your theory out is to see if you can generate the same curves that the FLRW metric does You can't afford to guess at those ratios of change as the expansion history and subsequently how each factor above evolves will depend on the evolution of each of the contributors above. The Cosmological calculator in my signature will greatly help generate a dataset for you using whichever cosmological parameters you choose. Unless you can produce each curve then your theory still requires significant work. It does anyways as you still need to prove it can prove how the universe seems to expand. You also haven't recognize that we don't rely on redshift and luminosity distance. We also use methods such as intergalactic parallax. -
Proton is a bit of a tricky devil as it revolves on the valence quarks two up and one down with a quark sea of indeterminant number of other quarks. Think of it as a quark gluon confined cloud
-
No G would not be different. Yes DM would likely be affected by Kerr metric frame dragging as it is affected by gravity just as any other particle. However it still won't clump in the same manner as baryonic matter due to lack of other field interactions such as the EM field.
-
One of the problems of the particle view is the electron spin taking the diameter that NTuft provided. The electrons angular momentum and that diameter. The electron angular momentum would end up exceeding the speed of light. If I recall the calculation correct it would be roughly 10 times c. The field excitation view with the increased radius this isn't the case. I mention this as it's one of the common arguments you will find that is used to support the field excitation view. Though certainly not the only argument. I should further mention that electron spin is intrinsic. It requires a 720 degree rotation to return to its original state so don't think of particles as little spinning balls.
-
The gravity effect only has the potential to reach into infinite range if the mass is infinite. For a BH the range that the gravity has a measurable effect is what's involved. That can determined by the r^2 relation.
-

On the Observational constrains of shrinking matter theories
Mordred replied to caracal's topic in Speculations
lets take this equation ask yourself what units is z ? (cosmological redshift equation) \[z = \frac{\lambda_r}{\lambda_e} - 1\] now this equation is only approximtely accurate when z<1 however it will diverge into a non linear curve. The other detail to note is that -1 included. lets look at your luminosity f'/f = 1/L^4 luminosity [W/m^2] is f the flux ? even then how did you derive that given the luminosity to distance is \[D_L=\sqrt{\frac{L}{4\pi F}}\] course the one that I find truly mysterious is how you get a length from temperature. Seems to me that you've assumed each of the values are going to have the same ratio of change with the scale factor and that is not the case. -
I agree @Capiertthere is absolutely no reason to have a few words on each line it makes your posts look like bad poetry please fill in the lines so everyone can actually follow what you are posting
-

On the Observational constrains of shrinking matter theories
Mordred replied to caracal's topic in Speculations
No I posted the graphs showing non linearity. The curves themselves are not linear. I'm sure you have heard the equation y=mx+b for linear graphs? A nonlinear function is a function whose graph is NOT a straight line. Its graph can be any curve other than a straight line. Does that help You still haven't fixed your dimensions in your equations they are still invalid as a result. Convert each unit to SI units on both the LHS and RHS of the equal sign. Follow the procedure in that link I provided lets take an example \[\frac{\acute{t}}{t}=L\] so \[\frac{s}{s}= metres\] wrong does not equal the seconds are on the LHS it doesn't have units of length which are on the RHS. -
The frame dragging follows the same 1/r^2 relation as that of the Newtons gravitational law
-

On the Observational constrains of shrinking matter theories
Mordred replied to caracal's topic in Speculations
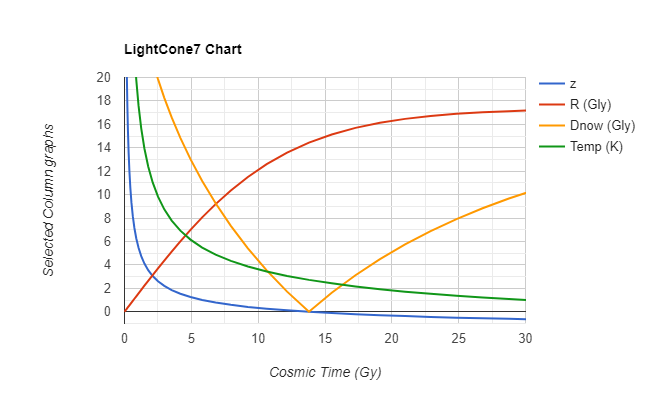
You might want to revisit your dimensional analysis.... You have in the above units units of length on the right hand side of your equations However no corresponding units of length on the left hand side in several of the above such as temperature, power, and luminosity secondly many of the above has non linear rates of change where you have linear. assuming you are dividing the primed value with the unprimed value then you have dimensionless quantities on the LHS. So the RHS definitely does not match in every case in the above. My point 5 is an example of a very distant set of measurements that can be examined using spectrographic evidence. Google Rydberg lines for what that entails. However when you account for redshift the lines show the same distance in the atomic orbitals. No you have not adequately accounted for that as your equations are too linear to handle the nonlinearity of redshift. this is what I am referring to on the nonlinearity note how Z as well as temperature suddenly spikes. Where distance now hits the x axis is the time now... previous to that is the past while to the right is the future using current cosmological parameters. You will also find that the expansion rate ie Hubble parameter is also non linear. In point of detail the above shows logarithmic rates of change. Zero on th x axis corresponds to z= 1100 CMB http://web.mit.edu/2.25/www/pdf/DA_unified.pdf use this and recheck all your equations under proper dimensional analysis -
True enough considering all the different variations coordinate time, proper time, conformal time, commoving time. Though in each case it's more accurate to treat these as defined observers.
-
Unfortunately it does relate in one regard as a common misconception is that a higher density past equates to spacetime curvature and hence time dilation with regards to the FLRW metric. However this isn't the case there is subtle differences in curvature with regards to the FLRW metric to spacetime curvature in GR with regards to time and proper time. Anyways that's likely best left off for a different discussion.