Eise

Thanks, Swansont, clear and concise. But I am afraid I still need a little help to see the consequences for experiments in the 'closed laboratory'. Rephrased: doesn't the invariance of the speed of light follow from the requirement that the laws of physics are exactly the same in every inertial frame? Say, I do experiments like the ones Faraday did, and I experimentally determine the strength of magnetic and electrical fields: based on the first postulate alone, I would say I cannot conclude that I am moving in relation to some absolute frame of reference. That means I would find the same values for u0 and e0 as in an absolute frame of reference. And then with Maxwell I can calculate the speed of light. And then, to think my point to the end, if I actually measure the speed of light, and find a different value than the calculated one I can only conclude that one of my presuppositions is false: u0 and e0 are dependent on my speed relative to an absolute frame of reference In my 'Maxwell theory' I have not accounted for my speed relative to an absolute frame of reference But both are in contradiction with the first postulate. So why I need the second postulate? Doesn't it follow from the first?

Sorry, I still have some problems with the terms 'invariant' and 'constant'. What is the difference, and how is this relevant for my example? If the speed of light would just be a constant, how would that effect my MM-experiment in my 'closed laboratory'? Could I then conclude from some experiment that my laboratory is moving? E.g. would I find the same Maxwell laws as an observer in rest, with a different value of c, or would I find different laws (with maybe the same value of c)? Could you elaborate a little?

Definitely not. Voigt, FitzGerald, Larmor, and as already mentioned by Strange, Poincaré, and Lorentz were some of the theoreticians that derived (parts of) the Lorentz transformations (why do you think they are called like that by Poincaré and, even by Einstein?). Einstein himself clearly stated that special relativity was so to speak 'in the air', waiting to be discovered. The problem is that some of them just derived correction factors to explain the null-result of the Michelson-Morleyor similar experiments, others could not get rid of the idea of a preferred frame of reference (the aether), especially Poincaré and Lorentz. Abraham Pais, in his biography of Einstein, Subtle is the Lord, even goes so far to say that Poincaré never really understood special relativity. But notwithstanding, Poincaré made important contributions, also about the mathematical properties of the Lorentz transformations. Many physicists were aware that there was a tension between classical mechanics and the electromagnetic theory of Maxwell, and tried to solve it. Einstein did it on basis of less premises than anybody else (the two postulates of SR), and so also got rid of the idea of a preferred frame of reference, i.e. the aether. For a (far from complete) overview, see History of special relativity. It is not just priority; it is definitely part of history of science, and as such, well, just interesting. How is it possible that people came to such counter-intuitive ideas? And that research is already done: read Pais.

What I personally do not understand is why it even needs the second postulate. Doesn't it follow logically from the first? The first postulate says, simplified (hopefully not too much simplified...) that in a 'closed laboratory', i.e. where it is not possible to 'look outside' , there is no experiment that tells you that you are moving. That means all laws of nature are exactly the same, including electromagnetism. Doesn't it follow that in a laboratory in an inertial frame one should always measure c for the velocity of light? If this were not the case, one could do a Michelson-Morley kind of experiment to determine one is moving.

geordief, Maybe Brian Cox, Why does E=mc2? is an interesting book for you. With a minimum of mathematics is makes plausible that: there is a cosmic speed limit that it turns out that this speed limit is the speed of light Of course it is not mathematically rigorous, but I think it is good enough.

So I was right. You should not teach SR because you do not understand SR, or even worse, you are thinking up wrong explanations. You can do two things: learn here what SR really is about keep in love with your pet theory, and, as you seem already have chosen to do, leave the forum.

I would say 'no'. I would say that in tensor formulation SR becomes wonderfully compact. But understanding tensors in themselves is another matter (I don't). If you are not 'fluent' with vectors and matrices, then the tensor way is definitely not easy. For a layman, sticking to simple algebra is the best way to understand SR. I wouldn't. I am sure it is a very good book, but it is a university level text book.

I have the German translation of Pais' Subtle is the Lord, so I will do my best. In the paragraph before the sentences I will try to translate, Abraham Pais discusses the new formalism of Minkowski, which obviously also included the use of tensors. Then Pais goes on, and says: (Quotes also in the original). As source, Pais refers to a personal conversation with V. Bargmann, of which Wikipedia says: So it seems Einstein was referring to the tensor formulation of special relativity, not to the description of spacetime by Minkowski.

I have: Abraham Pais, Subtle is the Lord, page 152. Einstein called Minkowski's 4-dimensional spacetime 'superfluous learnedness' (I just googled and only found a citation. I can look it up at home). Which of course is not exactly the same as: But it is close enough. I nowhere found something about 2 perpendicular sticks in Einstein's original article. I think you read more between the lines then there is room between them. I really doubt if you should teach others about relativity. As I see it you yourself miss basic understanding of SR. But I will postpone my judgement until I see how you answer Strange's question.

But why would things repeat exactly? I guess that it does not work like that. I think in an infinite, flat universe, you will find small areas (parts of space around a point) that are the same as the point where you left. But how big must such an area be to be exactly the same as where you left? I think infinitely large, otherwise they'd differ, namely at a finite distance, and so the points are not exactly the same, and therefore distinguishable. Maybe there is a way out if you look at the observable universe only: that is finite. If you would manage to travel faster than light and the expansion of the universe, you could travel outside our 'bubble' and enter completely distinct, but finite bubbles. Then it could work out. But that is of course not practicable...

Let's give it a try. dB is a logarithmic scale: every doubling of power means 3dB higher. let's take 101 dB as starting point. Just to give you an impression: So we have 999dB more. that is 333 steps of doubling. so 2333 is (100.30103)333 is about 10100. So about 10100 times more power in the sound then an impact wrench. That is pretty much, yes. (I hope I did not make a logical error here; it is a long, long time ago that I had to do with decibels and logarithms...).

As far as I remember, a type 1 'multiverse' is not really a multiverse: it is an infinite universe. An infinite, spherical universe does not make sense to me (but if some cosmologist knows that this would be meaningful I hope (s)he will chime in), but then we are still left with a flat universe, a parabolic or a hyperbolic universe. But you are right, nothing (at the moment!) points to a parabolic or a hyperbolic universe. And 'repeating' might be a to strong expression. One should always be very careful with 'infinity'. You cannot think about infinity as just a big number.

I wonder if you know yourself what you are asking. What has a flat plane to do with 'the idea of the multiverse' (which idea exactly? Many worlds theory? Bubbles in the inflational universe? Infinite universe with repeating patterns?). How can two points be indistinguishable and not be the same? If they are not the same, they are distinguishable per definition. (And how do points differ anyway?).

Keep calm 😉: Wild New Study Suggests The Universe Is a Closed Sphere, Not Flat

What about Hawking radiation? Such a small black hole would 'evaporate' immediately. But of course I doubt that one can describe electrons as 'nano black holes'. There seems to be no need for it in QED. And AFAIK at low energies an electron and a positron always annihilate as 2 photons. If that is true, I think it is not compatible with the idea of Hawking radiation.

Why not just read Wikipedia?

With a magnification of 10 times (or more) a walking bug, or even worse, a free flying dust particle or flying insect landing on a sensor or so, would also show that. The question really seems to me: did they see this just through one instrument, or through more, working on different principles, or even better, did they see it with the naked eye, or a simple eye piece? And even Hayek is not convinced that pilots are such good observers (I read recently, but I do not remember where). If I hear the pilot's excitement I do not hear any critical voice to check carefully what they see. My conclusion: too weak testimony to build any useful hypothesis. Did you apply Occam's razor? What is more probable: - a UFO really flying there, doing incredible things - an instrument with some dust particles or even an insect in it. If you know of any additional, independent observations from the same event, let us know.

It definitely looks like a speck of dust (or bug?) in the camera. I've some experience with photography, telescopes, microscopes, and this is very similar. Of course it is not on the objective, but somewhere else in the light path, maybe on the sensor. This depiction of course is not correct: From the videos I definitely do not get the impression of something flying there.

Nearly parallel. The rest is perspective, as in my picture with the grid.

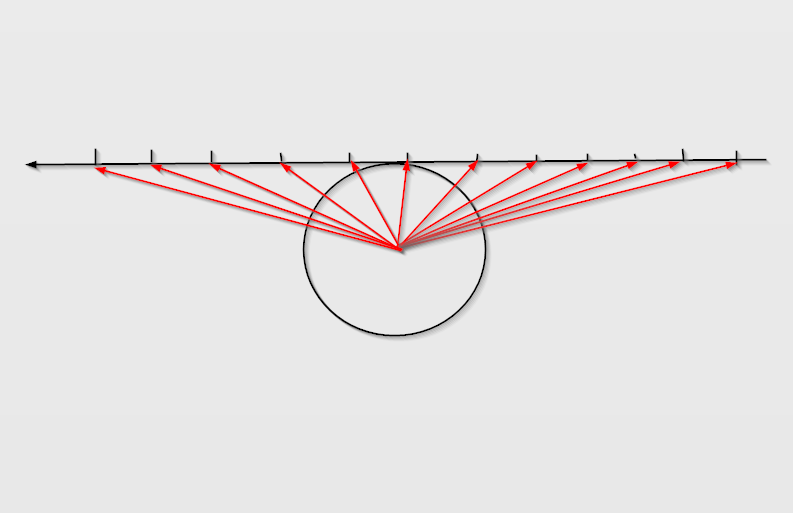
Yes, but they do not converge as you suggest. Therefor I drew my red arrows: from every point of the sun light is emitted and diverging. It is not my picture of course. But you see how the sunbeams seem to diverge from the sun, and then converge again at the opposite horizon? That is because the beams are nearly parallel.

You only react on half of my post. How do you explain the converging sunbeams opposite of the sun?

Because. First: the rays of the sun arrive here nearly parallel. But if they would be parallel, they would perspectively converge to one point, as my picture shows. So second: you interpret your own picture wrong: the rays you see coming from the sun are not spreading, they are nearly pointed at you, they just go over your head, left of you, in front of you etc. But they do not radiate perpendicular to the sun's surface. Your sketch is wrong. I drew a few examples of what really is going on: But of course you do not see the light rays that miss the earth (in the end you can't see2 light if it doesn't enter your eyes). And last but not least, if you look into the opposite direction of the sun, you also see the sun beams converge: From here. It also explains it: With a fish eye objective: You do as the people who thought the earth is in the middle of the solar system: we do not feel the turning of the earth, we see the sky turn around us, so everything is turning around us.

So again: why would that lead to you observing photons getting faster?

Because it behaves like the bike (have you clicked the link?). The photons must accelerate because the bike does??? And no, I did not look at the link, because it is on facebook. It looks like that, but it isn't. The bike looks smaller, but it is not. 'As observed', yes, but not in reality. The poles look closer to each other, but they are not. If you from your position could see how many poles the bike would pass per time, it would not change. The only thing you do is describing the movement of the bike in polar coordinates. But a constant velocity, described in polar coordinates, does not lead to a constant angular velocity. A change of coordinate system does not change what is actual occurring. You did not argue for your view point, that's why I am asking: why do 'photons that reach your eyes must appear accelerated'? Under these circumstances Swansont's 'No' suffices. Does this drawing help?

One minute physics has a video about it: Why It's HARD To Land on Mars