-
Posts
586 -
Joined
Content Type
Profiles
Forums
Events
Everything posted by Commander
-
Plz use password Thomas Walker to read the document Life Everlasting.pdf
- 1 reply
-
-4
-
The Prime Minister ! Do not feel Bad that you are Not a Prime Minister ! You are indeed more than a Prime Minister of your Closest Nation ! The name of the Nation is your Own Name consisting of so many Living Cells and Organs and Systems that make Yourself ! You are the Custodian, Care Taker, The Boss, the CMD , the CJI ,the President and everything and Everyone in Position for this Body ! Of Course you also need to be the House Keeper, Cleaner, Errand Runner and Duty Staff for this Nation ! You need to Listen to and Act/Decide over the Demands and Cries of each System and Organ that Comprises you ! Highly Complicated Technical and of course more Intelligent than all the latest AI Systems invented by Human Beings your Systems are ! What you achieve in Life depends on how you perform your Functions ! Wish you all the very Best !
-
Hi toucana TY for sharing your ideas and thoughts ! I have been playing Contract Rubber Bridge and thereafter Duplicate Bridge Tournament Bridge for over 50 years ! BBO is the main site which is popular online. Nowadays great care is taken to keep Bridge as a Non-Gambling Money handling Game and all avenues giving out real Money have been shut down I have played a lot on Top Bridge, bridgeHit, BridgeBig and also MoneyBridge on BBO [now shut down] over the past 30 years as well as local Club/National Tournaments ! According to me the most important aspects of online Gaming is genuine randomness. Total Honesty and transparency which is missing in every Gaming Portal on earth ! I am sharing my ideas and thoughts here but I request Hecklers and Negative markers to keep away and the one regret I have about this forum is that their Rating System is Totally Unjust allowing Enemies to derate and known group to overrate others and if I was someone like Trump I would have used stronger words here !
-
Further Dialogues and discussions on WhatsApp Business [11:52 am, 1/1/2025] Chai BC: Interesting [12:10 pm, 1/1/2025] T W: Let not the Chinese be the first to take up my idea and bring out the Product 😊 [12:13 pm, 1/1/2025] T W: TY Chai 🙏 [1:07 pm, 1/1/2025] T W: Another advantage is Robots can be players or substitutes too [1:38 pm, 1/1/2025] T W: In the case of Rummy a round table will be employed with provision for multiplayers This can revolutionise the entire Card Games and Tournaments [4:28 pm, 1/1/2025] Chai BC: Can we build a prototype [7:58 pm, 1/1/2025] T W: Why not. We can think of that [7:59 pm, 1/1/2025] T W: I rang up to wish you Happy New Year [5:55 am, 2/1/2025] Chai BC: Happy New Year to you too!... C u at the bridge room soon 🙏 [8:08 am, 2/1/2025] Mannan: Good morning sir. What is the final objective of this project? [8:15 am, 2/1/2025] T W: Maybe we can take up the Development in a National Level Researchers' Competition which will bring Bridge in the Lime Light increasing the National Awareness and Research in General and pave way for Indian Team to become world Champions [recently they came 2nd] [1:57 pm, 1/1/2025] Ramanand Baliga: True, but card players love the feel of cards, arranging them, playing actual card when their turn comes. Same as BBO versus playing in person with friends [2:01 pm, 1/1/2025] T W: I understand Yes ! [3:57 pm, 1/1/2025] T W: Give up some Take some [8:07 am, 2/1/2025] T W: To enhance the Card Playing Feel and Pleasure we can also come out with an RFID based new Generation cards Pack which can be monitored and used for Shuffle Cut and Deal and thereafter played on by Humans holding the cards in their hands and doing what exactly they otherwise do ! This will have Software Tools including AI Tools under the Control of the Server. This can be used standalone eliminating the requirement of Digital Touch display or can be used in conjunction with the Bridge Table appropriately ! 👍 [8:23 am, 2/1/2025] Ramanand Baliga: Computer won't allow revoke to be committed by a human player. [8:43 am, 2/1/2025] T W: No it will allow revoke to happen (in case of RFID cards) but record it and take action Setting can also be allowed to give Warning or Prevent it ! [8:45 am, 2/1/2025] T W: Computer Director can speak to the table too [9:18 am, 2/1/2025] Ramanand Baliga: Good design. 🙏 [1:03 am, 2/1/2025] Pratap: Work on it Walker. Good luck! [10:35 am, 2/1/2025] T W: TY 🙏 Now that I have broadcast the idea thinking of going for a National level Product Design Competition [2:56 pm, 2/1/2025] Walker… 😎 Amit Walker…: Hi daddy, Happy New Year 2025 again… In this new year why don’t you try developing & implementing some of your ideas… Because ideas will just be ideas till they are implemented… And they can be done your way… Because the best part of when I do something, is I get to do it my way with my own ideas, irrespective of what anyone else’s ideas might be since I will do only what I would like to do when I do… 🙂 [9:23 am, 7/1/2025] T W: TY Amit Very true but as I have shared the ideas with many I am thinking of instituting a National level or International level of Product Development Competition in which Researchers and Students can participate and we can have a panel to assess them and assist them in the development This will also popularise Bridge and generate Awareness [9:26 am, 7/1/2025] T W: I need some support from Organisations and Individuals Maybe you or Ajit too can pitch in [12:05 pm, 7/1/2025] Walker… 😎 Amit Walker…: Nobody works for free anymore daddy… 🙂 Even if you call it a competition… I have too many ideas of my own, and too little time to spare for them itself, so not sure if I would be of much help… But I will always be able to help by sharing my thoughts and ideas whenever it might be needed…
-
The Next Generation Bridge Table Thomas Walker 31 Dec 2024 Copy Right I have thought of this about 15 years back when the Computer Displays and Touch Functions were evolving The Table and Chairs set will be almost like the present setup Five Displays one Square Top and four matching rectangular side Panels which can be folded down for being visible to only that Player. Improvements can be made to make the side Panels Detachable to br held in hand On the Top Display Touch enabled Buttons for Deal Creation,Shuffle,Cut,Deal,Bidding Boxes,Storing Bids, Played Cards,Trick Counts etc enabled displayed and oriented according to Bridge Rules and authorised viewership ! Play starts after deals created and displayed on the individual Panels and Biddings done and Opening Leader designated. Also Deals can be created / generated or picked up from the Server all wireless networked and used on the Specific Table/s [Multiple Tables for a Tournament can be networked] The opening leader clicks on the card he wants to play on his panel which gets removed from his panel and goes and falls in the middle of the table followed by other players in their turn doing so and at the end of the trick the winner is enabled to collect etc as any Bridge or Card Player can Imagine and understand ! All features of BBO can be adopted !! It’s very SIMPLE !!! These Tables can be used for Whist and other card games too !
-
Thomas Walker 31 Oct 24 Bangalore I tried to keep what I am going to say to myself but couldn’t It’s mind boggling and truly encouraging and therefore plz do share with them you care for It happened yesterday night/early morning I hit the bed earlier than usual yesterday night and I was feeling tired and uncomfortable My nose block sinus and mucus gave me trouble Dryness in the mouth and difficulty in breathing ensued Remember I had posted before that Clenching Fist during your waking hours and invoking God’s Power can Solve and improve all your problems and situations provided you apply it assiduously and constantly Then why did I reach this state Well I must admit that this Key did work always and you must apply it ceaselessly That is where is the catch Many times as you are up and about doing your chores routines and pastimes you get into the state of exhaustion and calculations and mental exercise and forget to apply the Key all along Now getting out of this state is tough As I tried all things and kept drinking water normal breathing and comfortable Sleep couldn’t be achieved Then only I applied the Key as the last resort and invoked God’s Power Clenching the Fists and totally and prayerfully seeking God’s Cure and Restoration After about 5 minutes I had attained normalcy and the breathing was easy and smooth Praise the Lord ! My wife would have wondered what has happened to him and suddenly after 2 AM how come he is all quiet and resting Indeed it was truly miraculous After denying and debating for a long time I had agreed to go for Consultations at an Ayurvedic Clinic at 3PM today (about 2hrs to go at the time of writing this) I have now cancelled it. I was about to post this first thing in the morning but had to hold it for a while After a couple of hours I could see that slight nose flow was felt which discouraged me a bit but then I realised God’s Power can not only stabilise but reverse and eradicate the cause itself and no harm in clearing the Sinus if that is God’s Will ! Constant Seeking and Invoking God’s Healing Touch and Power is the Only Way for Wholesome Health and Life TY Rgds May God Bless !
- 4 replies
-
-3
-
*Clench your Fist and Live On !* 3 Oct 24 Bangalore The revelation has come to me that if we clench our fist and live through and face Situations during our Waking Hours it turns out to be a Life preserving Exercise and a Siilent Healer ! *Analysis* We see that from Childhood Human Beings face newer changing and hazardous situations and the Child that handles it well steadfastly without giving up with a Clenched Fist is the Successful one in Life. Generally in older ages this exercise is forgotten or given up during Testing Situations which lets in Deterioration in Health along with Aging ! This can only be reversed by adopting the right exercise !! Therefore I have adopted this and it has been greatly beneficial to me ! Even issues like dry skin Cracked Heels nose block/mucus etc are getting rid off as a result without medicines !!! It may be due to increased blood circulation and BP control. This is why I am telling this to all 😊 With best wishes and regards Thomas Walker PS : Please share this with as many as possible
- 4 replies
-
-1
-

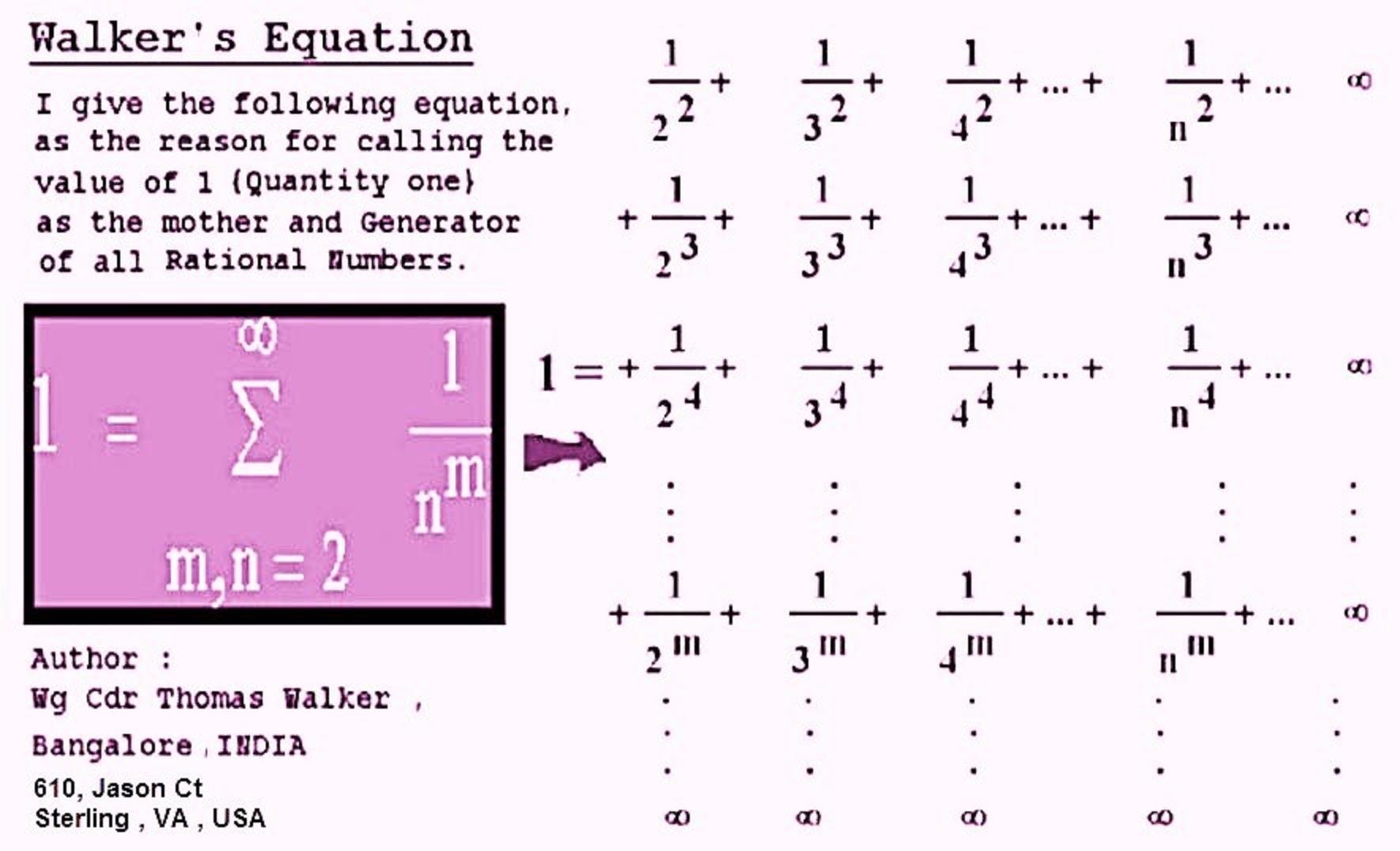
Geometric Model of Walker's Equation and Walker's Series !
Commander replied to Commander's topic in Mathematics
-

Geometric Model of Walker's Equation and Walker's Series !
Commander replied to Commander's topic in Mathematics
To Summarize : 1 = 1/1x2 + 1/2x3 + 1/3x4 + ……. + 1/(n-1) x n + 1/n(n+1) + 1/(n+1)(n+2) + 1/(n+2)(n+3) + ………. 1 - (1/1x2 + 1/2x3 + 1/3x4 + ……. + 1/(n-1) x n ) = 1/n(n+1) + 1/(n+1)(n+2) + 1/(n+2)(n+3) + ………. Which is 1/n = 1/n(n+1) + 1/(n+1)(n+2) + 1/(n+2)(n+3) + ………. Therefore 1 = n/n(n+1) + n/(n+1)(n+2) + n/(n+2)(n+3) + ………. OR 1 = 1/(n+1) + n/(n+1)(n+2) + n/(n+2)(n+3) + ………. 13 Sep 2024 -

Geometric Model of Walker's Equation and Walker's Series !
Commander replied to Commander's topic in Mathematics
We see that while 1 = ½ + 1/2x3 + 1/3x4 + 1/4x5 ……… It also validly sums up for every n terms Ie 1 = ½ + 1/2 for n=2 1 = ½ + 1/2x3 + ⅓ for n=3 1 = ½ + 1/2x3 + 1/3x4 + ¼ for n=4 1 = ½ + 1/2x3 + 1/3x4 + 1/4x5 + ⅕ for n=5 etc OK TY I understood what you said and what you mean ! Thanks ! I can make out many explanations are a bit difficult to understand from the depiction and notes but I can vouch I can explain it more clearly if someone wants to know ! -

Geometric Model of Walker's Equation and Walker's Series !
Commander replied to Commander's topic in Mathematics
Let’s take a look into the Geometrical Model which has horizontal lines drawn at ½, ⅓, ¼ etc upto infinity The area below each line is same value inn sq units that is ½,⅓,¼, etc Each one of these are also equal to 1/1x2 , 2/2x3, 3/3x4, etc And each has a power expansion of (⅓ + ⅓^2 +⅓^3 …) , (¼ + ¼^2 + ¼^3 ….) . (⅕ + ⅕^2 +⅕^3 ….. ) And now. The area below each line is the sum of all rectangles below it : That is ½ = 1/2x3 + 1/3x4 + 1/4x5 …… ⅓ = 1/3x4 + 1/4x5 + 1/5x6 ……. ¼ = 1/4x5 +1/5x6 + 1/6x7 …….. Etc And therefore the Walker’s Series is proved as 1 = 2/2x3 + 2/3x4 + 2/4x5 …….. 1 = 3/3x4 +3/4x5 + 3/5x6 ……… 1 = 4/4x5 + 4/5x6 + 4/6x7 ……… By Wg Cdr Thomas Walker Bangalore India 11 Sep 24 -

Geometric Model of Walker's Equation and Walker's Series !
Commander replied to Commander's topic in Mathematics
This is some recognition I got in a paper when I was putting up my findings in some University websites -

Geometric Model of Walker's Equation and Walker's Series !
Commander replied to Commander's topic in Mathematics
Walker's Equation by Wg CdrThomas Walker.pdfWgCdrThomasWalkersTheories.pdfWalker's Equation.docWalkerEqn Jim Loy.docACuriousConnection.pdf Now with these basic Structures indicated I believe that Logically , Algebraically and by Mathematical Induction we can expand these equations to explore and detect other Relations involving numbers other than Integers ! BTW Some of these old documents may contain my old Contact details My present address Flat # 003 Sai Excellency Apartments 2nd Cross Hennur main road Bangalore 560043 India Phone 9880184818 and 8884577768 both having WhatsApp -

Geometric Model of Walker's Equation and Walker's Series !
Commander replied to Commander's topic in Mathematics
-

Geometric Model of Walker's Equation and Walker's Series !
Commander replied to Commander's topic in Mathematics
Hi Joigus TY Earlier I had given the proof of Walker’s Equation and now I have depicted the Proof Geometrically as can been seen both for Summing upto 1 and converging The same depiction also indictes the Geometric representation of Walker’s Series for those who can visualise ! The General form of Walker’s Series for n from 1 to infinity can also be inferred from this ! If I write up more on this I will put up here ! We can see 1/n = 1/(n+1) + 1/(n+1)^2 + 1/(n+1)^3 + …… as per Walker’s Equation Proof Steps. Which is : 1/n - 1/n+1 = inverse powers of (n+1) from 2 to infinity as shown above which can be called RHS The LHS is 1/n - 1/n+1 = 1/n(n+1) And this progression goes on …….. The LHS a Linear sum of Factors adds up to 1 and the RHS a double matrix depiction of inverse powers adds up to 1 too ! The LHS gives rise to the Walker’s Series and the RHS gives rge Walker’s Equation ! Hi Yes Harmonic Series is Divergent but Walker’s Series is not divergent. No member of the Series has a value of more than 1/(n+1) and no FACTOR used in the Equation will be less than ‘n’ in value either in Denominator or Numerator. 1 = n/n(n+1) + n/(n+1)()n+2) + n/(n+2)(n+3) + …….. If n = 1 : then 1/1x2 + 1/2x3 + 1/3x4 + ……… As n increases 1= 2/2x3 + 2/3x4 + 2/4x5 + ………. Similarly 1 = 3/3x4 + 3/4x5 + 3/5x6 + ……. 1 = 4/4x5 + 4/5x6 + 4/6x7 + ……….. . . . -

Geometric Model of Walker's Equation and Walker's Series !
Commander replied to Commander's topic in Mathematics
Hi Yes Harmonic Series is Divergent but Walker’s Series is not divergent. No member of the Series has a value of more than 1/(n+1) and no FACTOR used in the Equation will be less than ‘n’ in value either in Denominator or Numerator. 1 = n/n(n+1) + n/(n+1)()n+2) + n/(n+2)(n+3) + …….. If n = 1 : then 1/1x2 + 1/2x3 + 1/3x4 + ……… As n increases 1= 2/2x3 + 2/3x4 + 2/4x5 + ………. Similarly 1 = 3/3x4 + 3/4x5 + 3/5x6 + ……. 1 = 4/4x5 + 4/5x6 + 4/6x7 + ……….. . . . -

Geometric Model of Walker's Equation and Walker's Series !
Commander replied to Commander's topic in Mathematics
1 = 1/(n+1) + n/(n+1)(n+2) + n/(n+2)(n+3) + n/(n+3)(n+4) …. etc till infinity For any n (positive integer) from 1 to infinity This may be called Walker’s Series’ By Wg Cdr Thomas Walker - 22 Aug 2024 FYI plz -
Hi I give here the Geometric Model and representation of Walker's Equation and proposal of an Equation od Infinite Series which I call 'Walker's Series' which appears to have escaped many ! Proof of Walker's equation.docx - Google D Dear Moderator, I tried to remove the duplicate images in this post but couldn't succeed Plz remove the repeating pics TY !
-
The area is around 0.0913 Pi/6 - (Sqrt 3 /4) Using Pi = 22/7 gets this result !
-
The strip shown has two sides : A straight line of 1 Unit Length and an arc from a Circle having a radius of 1 Unit ! The diagram is shown below. Find the Area of the Strip in Square Units of the same Unit !
-
A land owner inherits a Circular Piece of land and shares it with his siblings and children ! He lays out four plots of identical shape having 1/11 (one eleventh) of the total land and four other identical plots each having area of 1/4 Square kilometre each. He retains for himself a Square Plot of 1 Square kilometre ! You are required to show the layout of how he did it specifying the dimensions !
-
Yes TY all for answers ! Pi/6 is the Fraction and 3xSqr Rt 3 times is the Volume of the Bigger Sphere to that of the Smaller one ! Quite Straight forward !
-
If *C* is a Cube and *S1* is the Sphere Inscribed and *S2* is the Sphere Superscribed then (1) What is the fraction of the volume of *C* is contained in *S1* (2) How many times the volume of *S2* is that of *S1*