Commander

Thomas Walker 31 Oct 24 Bangalore I tried to keep what I am going to say to myself but couldn’t It’s mind boggling and truly encouraging and therefore plz do share with them you care for It happened yesterday night/early morning I hit the bed earlier than usual yesterday night and I was feeling tired and uncomfortable My nose block sinus and mucus gave me trouble Dryness in the mouth and difficulty in breathing ensued Remember I had posted before that Clenching Fist during your waking hours and invoking God’s Power can Solve and improve all your problems and situations provided you apply it assiduously and constantly Then why did I reach this state Well I must admit that this Key did work always and you must apply it ceaselessly That is where is the catch Many times as you are up and about doing your chores routines and pastimes you get into the state of exhaustion and calculations and mental exercise and forget to apply the Key all along Now getting out of this state is tough As I tried all things and kept drinking water normal breathing and comfortable Sleep couldn’t be achieved Then only I applied the Key as the last resort and invoked God’s Power Clenching the Fists and totally and prayerfully seeking God’s Cure and Restoration After about 5 minutes I had attained normalcy and the breathing was easy and smooth Praise the Lord ! My wife would have wondered what has happened to him and suddenly after 2 AM how come he is all quiet and resting Indeed it was truly miraculous After denying and debating for a long time I had agreed to go for Consultations at an Ayurvedic Clinic at 3PM today (about 2hrs to go at the time of writing this) I have now cancelled it. I was about to post this first thing in the morning but had to hold it for a while After a couple of hours I could see that slight nose flow was felt which discouraged me a bit but then I realised God’s Power can not only stabilise but reverse and eradicate the cause itself and no harm in clearing the Sinus if that is God’s Will ! Constant Seeking and Invoking God’s Healing Touch and Power is the Only Way for Wholesome Health and Life TY Rgds May God Bless !

*Clench your Fist and Live On !* 3 Oct 24 Bangalore The revelation has come to me that if we clench our fist and live through and face Situations during our Waking Hours it turns out to be a Life preserving Exercise and a Siilent Healer ! *Analysis* We see that from Childhood Human Beings face newer changing and hazardous situations and the Child that handles it well steadfastly without giving up with a Clenched Fist is the Successful one in Life. Generally in older ages this exercise is forgotten or given up during Testing Situations which lets in Deterioration in Health along with Aging ! This can only be reversed by adopting the right exercise !! Therefore I have adopted this and it has been greatly beneficial to me ! Even issues like dry skin Cracked Heels nose block/mucus etc are getting rid off as a result without medicines !!! It may be due to increased blood circulation and BP control. This is why I am telling this to all 😊 With best wishes and regards Thomas Walker PS : Please share this with as many as possible

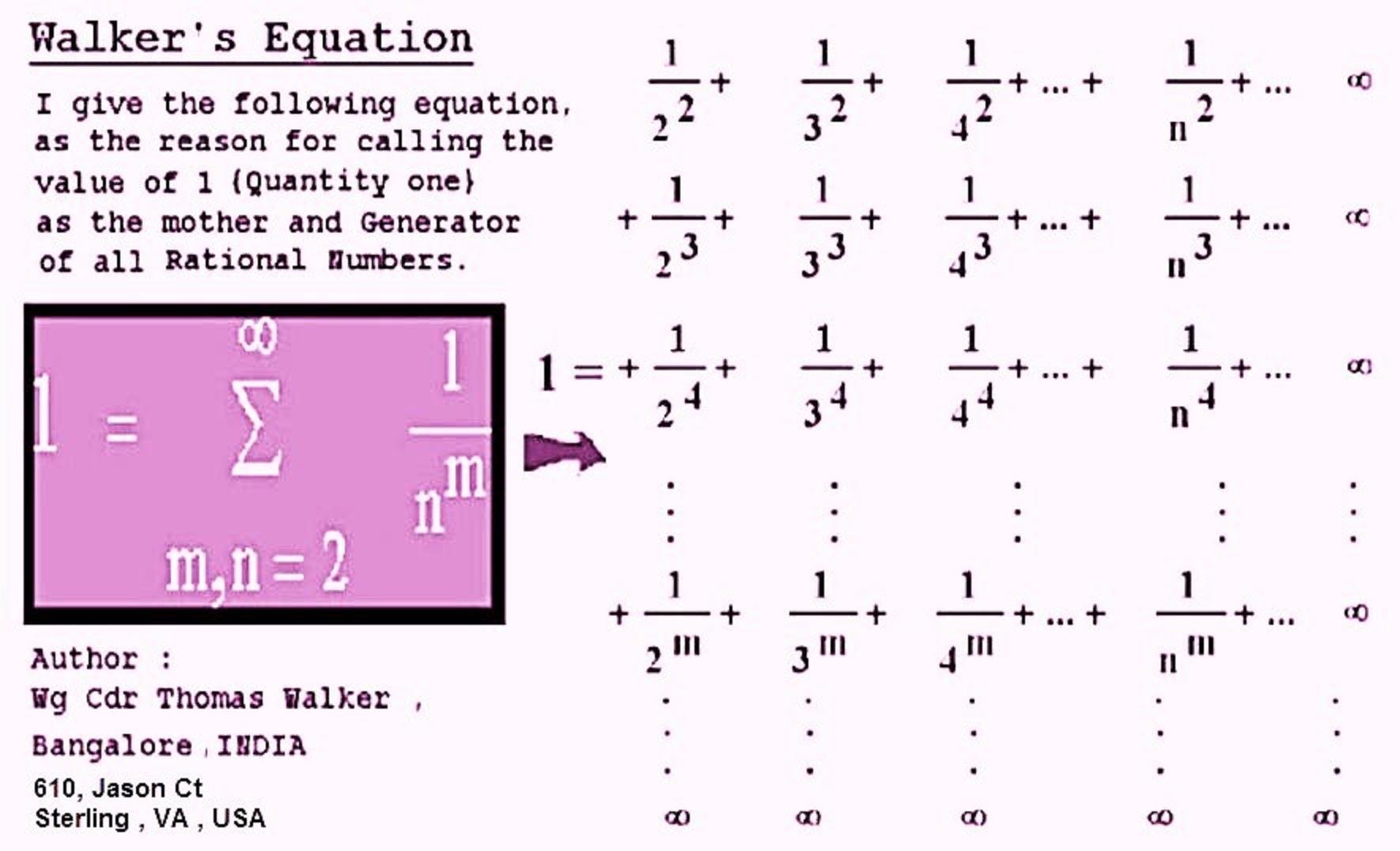
To Summarize : 1 = 1/1x2 + 1/2x3 + 1/3x4 + ……. + 1/(n-1) x n + 1/n(n+1) + 1/(n+1)(n+2) + 1/(n+2)(n+3) + ………. 1 - (1/1x2 + 1/2x3 + 1/3x4 + ……. + 1/(n-1) x n ) = 1/n(n+1) + 1/(n+1)(n+2) + 1/(n+2)(n+3) + ………. Which is 1/n = 1/n(n+1) + 1/(n+1)(n+2) + 1/(n+2)(n+3) + ………. Therefore 1 = n/n(n+1) + n/(n+1)(n+2) + n/(n+2)(n+3) + ………. OR 1 = 1/(n+1) + n/(n+1)(n+2) + n/(n+2)(n+3) + ………. 13 Sep 2024

We see that while 1 = ½ + 1/2x3 + 1/3x4 + 1/4x5 ……… It also validly sums up for every n terms Ie 1 = ½ + 1/2 for n=2 1 = ½ + 1/2x3 + ⅓ for n=3 1 = ½ + 1/2x3 + 1/3x4 + ¼ for n=4 1 = ½ + 1/2x3 + 1/3x4 + 1/4x5 + ⅕ for n=5 etc OK TY I understood what you said and what you mean ! Thanks ! I can make out many explanations are a bit difficult to understand from the depiction and notes but I can vouch I can explain it more clearly if someone wants to know !

Let’s take a look into the Geometrical Model which has horizontal lines drawn at ½, ⅓, ¼ etc upto infinity The area below each line is same value inn sq units that is ½,⅓,¼, etc Each one of these are also equal to 1/1x2 , 2/2x3, 3/3x4, etc And each has a power expansion of (⅓ + ⅓^2 +⅓^3 …) , (¼ + ¼^2 + ¼^3 ….) . (⅕ + ⅕^2 +⅕^3 ….. ) And now. The area below each line is the sum of all rectangles below it : That is ½ = 1/2x3 + 1/3x4 + 1/4x5 …… ⅓ = 1/3x4 + 1/4x5 + 1/5x6 ……. ¼ = 1/4x5 +1/5x6 + 1/6x7 …….. Etc And therefore the Walker’s Series is proved as 1 = 2/2x3 + 2/3x4 + 2/4x5 …….. 1 = 3/3x4 +3/4x5 + 3/5x6 ……… 1 = 4/4x5 + 4/5x6 + 4/6x7 ……… By Wg Cdr Thomas Walker Bangalore India 11 Sep 24

This is some recognition I got in a paper when I was putting up my findings in some University websites

Walker's Equation by Wg CdrThomas Walker.pdfWgCdrThomasWalkersTheories.pdfWalker's Equation.docWalkerEqn Jim Loy.docACuriousConnection.pdf Now with these basic Structures indicated I believe that Logically , Algebraically and by Mathematical Induction we can expand these equations to explore and detect other Relations involving numbers other than Integers ! BTW Some of these old documents may contain my old Contact details My present address Flat # 003 Sai Excellency Apartments 2nd Cross Hennur main road Bangalore 560043 India Phone 9880184818 and 8884577768 both having WhatsApp

Hi Joigus TY Earlier I had given the proof of Walker’s Equation and now I have depicted the Proof Geometrically as can been seen both for Summing upto 1 and converging The same depiction also indictes the Geometric representation of Walker’s Series for those who can visualise ! The General form of Walker’s Series for n from 1 to infinity can also be inferred from this ! If I write up more on this I will put up here ! We can see 1/n = 1/(n+1) + 1/(n+1)^2 + 1/(n+1)^3 + …… as per Walker’s Equation Proof Steps. Which is : 1/n - 1/n+1 = inverse powers of (n+1) from 2 to infinity as shown above which can be called RHS The LHS is 1/n - 1/n+1 = 1/n(n+1) And this progression goes on …….. The LHS a Linear sum of Factors adds up to 1 and the RHS a double matrix depiction of inverse powers adds up to 1 too ! The LHS gives rise to the Walker’s Series and the RHS gives rge Walker’s Equation ! Hi Yes Harmonic Series is Divergent but Walker’s Series is not divergent. No member of the Series has a value of more than 1/(n+1) and no FACTOR used in the Equation will be less than ‘n’ in value either in Denominator or Numerator. 1 = n/n(n+1) + n/(n+1)()n+2) + n/(n+2)(n+3) + …….. If n = 1 : then 1/1x2 + 1/2x3 + 1/3x4 + ……… As n increases 1= 2/2x3 + 2/3x4 + 2/4x5 + ………. Similarly 1 = 3/3x4 + 3/4x5 + 3/5x6 + ……. 1 = 4/4x5 + 4/5x6 + 4/6x7 + ……….. . . .

Hi Yes Harmonic Series is Divergent but Walker’s Series is not divergent. No member of the Series has a value of more than 1/(n+1) and no FACTOR used in the Equation will be less than ‘n’ in value either in Denominator or Numerator. 1 = n/n(n+1) + n/(n+1)()n+2) + n/(n+2)(n+3) + …….. If n = 1 : then 1/1x2 + 1/2x3 + 1/3x4 + ……… As n increases 1= 2/2x3 + 2/3x4 + 2/4x5 + ………. Similarly 1 = 3/3x4 + 3/4x5 + 3/5x6 + ……. 1 = 4/4x5 + 4/5x6 + 4/6x7 + ……….. . . .

1 = 1/(n+1) + n/(n+1)(n+2) + n/(n+2)(n+3) + n/(n+3)(n+4) …. etc till infinity For any n (positive integer) from 1 to infinity This may be called Walker’s Series’ By Wg Cdr Thomas Walker - 22 Aug 2024 FYI plz

Hi I give here the Geometric Model and representation of Walker's Equation and proposal of an Equation od Infinite Series which I call 'Walker's Series' which appears to have escaped many ! Proof of Walker's equation.docx - Google D Dear Moderator, I tried to remove the duplicate images in this post but couldn't succeed Plz remove the repeating pics TY !

The area is around 0.0913 Pi/6 - (Sqrt 3 /4) Using Pi = 22/7 gets this result !

The strip shown has two sides : A straight line of 1 Unit Length and an arc from a Circle having a radius of 1 Unit ! The diagram is shown below. Find the Area of the Strip in Square Units of the same Unit !

A land owner inherits a Circular Piece of land and shares it with his siblings and children ! He lays out four plots of identical shape having 1/11 (one eleventh) of the total land and four other identical plots each having area of 1/4 Square kilometre each. He retains for himself a Square Plot of 1 Square kilometre ! You are required to show the layout of how he did it specifying the dimensions !

Yes TY all for answers ! Pi/6 is the Fraction and 3xSqr Rt 3 times is the Volume of the Bigger Sphere to that of the Smaller one ! Quite Straight forward !

If *C* is a Cube and *S1* is the Sphere Inscribed and *S2* is the Sphere Superscribed then (1) What is the fraction of the volume of *C* is contained in *S1* (2) How many times the volume of *S2* is that of *S1*

E = M C 2 That is : E >>> Energy | Ego | Eminence M >>> Mind | Mobility | Maturity C >>> Creativity | Conscience | Courage

Need to cut like that !

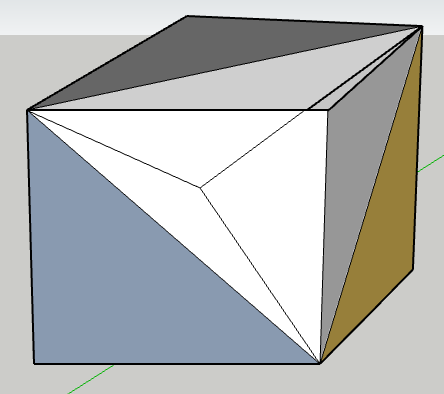
You need to chop of four corners with an equilateral triangle as the base with sides of diagonals Four of them That leaves a tetrahedron in the middle We need to cut it in four equal parts with each equilateral triangular base (four of them) and apex meeting at the center of the cube The four earlier cut pieces (cut for the sake of explanation) are merged with equal area bases of the four pieces of the tetrahedron

Also all the faces of the pieces must be TRIANGLES ! Sorry I forgot to mention this !

Please note it is four pieces and not six ! Error regretted !!

Cut a Cube into six identical pieces each having nine edges !