Everything posted by Trurl
-
Why do I do science?
I do believe in doing science. I just wanted to point out the dilemma. It is the same in business. And politics. I guess you just have to make the best decisions you can. Some stuff is small but with others you have to rely on intuition. Many years ago I was put into a small leadership position of a group of 20 people. I was never in a leadership position before and it showed. I was an engineer student and I thought in my l leadership role that would help me “think” about all our decisions. I was wrong. Managing people, completing objectives, and making decisions is a whole other skill set. I just wanted to point out science is also limited. You guys have good answers, but more than science applies with decisions. We can’t be responsible for what is done with our creations or can we? I don’t like when science is referred to as a religion or do I think as Christianity as one. Instead they are a set of beliefs we base our decisions on. In my beliefs I don’t think we are any more in control with science. There is just too much unknown. By being out of control in science I mean we are not in total control when creating something. That is not me saying that. It comes from book on Creativity and Flow. Some decisions are insignificant but even if we are just a scientist creating or someone using that scientist’s knowledge we better make the best decision possible. Those are my thoughts. Like I said you guys did give good answers. I am under the assumption that science directly relates to technology. I have never experienced it otherwise. Just as some discredit Christianity with studying it, I am lost when science doesn’t result in knowledge or technology. The fruit of knowledge is what caused all these problems in the first place.😉 You guys are right curiosity is a good thing. The odds are that man eats the apple every time.
-
Why do I do science?
Why do I do science? I just replied to a tweet on Twitter with the following tweet: Science and money both solve problems. But both cause new problems. Like winning a 100 million then going bankrupt or building a bomb and causing arms race. Blatant example where science doesn’t solve anything. Don’t get me wrong I have loved science all my life. But what is its underlying meaning or goal? Fix one problem; five new ones. Ones that don’t exist before the science. I ask before if a utopian world could exist through science but I couldn’t define utopian. But those who answered said they did science to improve the World. I like that answer, but when tweeting the above made me wonder why I do science? I should include a link to the tweet. The original tweet the author talk about how we use technology to track the entire internet and the computer scientists would rollover in their grave if they knew what their technology was being used for. When I say,”why do I do science?” I am not trying to trash science. I just wonder is it doing what we intend it to and are we even in control of it?
-
Simple yet interesting.
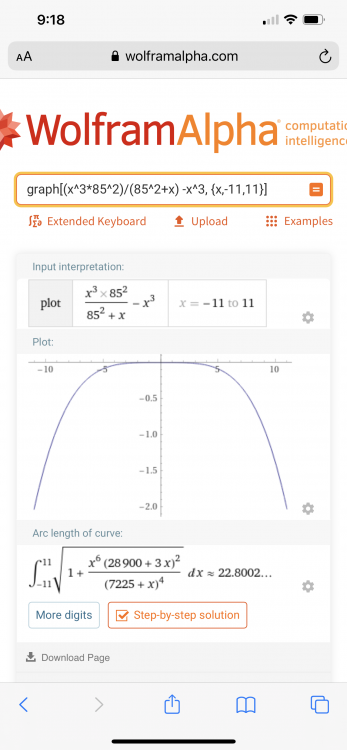
Ok you want a pattern. I saw a post here about a debate if math was created or invented. The same applies to patterns. The subconscious defines the pattern. I say a pattern is a pattern. I look for them. And share them with the goal that others will see them too. But the fact is you should see the same pattern. Maybe someone has seen the pattern and is keeping it secret. In the hands of a capable mathematician this could be an attack on RSA. But take the previous equation x^3 approx - x^3 And plug in a known x, say my favorite 5. Let pnp = the y value of the graph The hypothesis is that x of the graph will approach an x of zero where pnp of y equals a semiPrime. In other words, when x =0 you will find every SemiPrime that has a factor of 5 will be found. (You can invert x and y for y =0 so that the graph is y=f(x).)
-
Simple yet interesting.
No you are right there is no pattern in Primes in this graph. Instead it shows the value of the smaller semi-Prime. Pnp =x*y. x^3 approximate -x^3 We subtract to make x appear around y equals zero so we know where to look for it. The pattern of Primes comes from graphing all pnp’s. If you know a number is a factor of a semi-Prime you know it is Prime. I did not show that in the last graph. The last graph is to factor the semi-Prime.
-
Simple yet interesting.
-
Simple yet interesting.
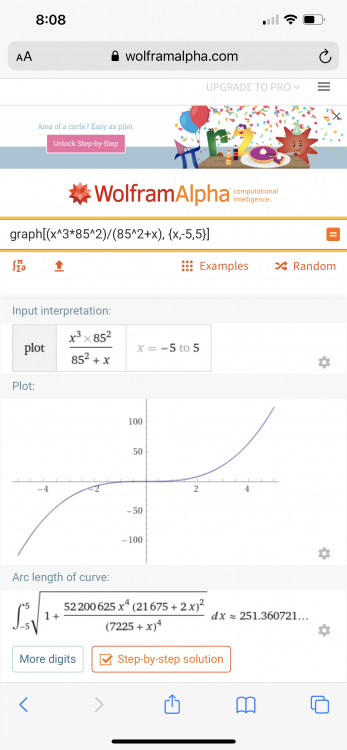
There are 2 patterns. The one found in this graph where all possible x’s are graphed against a know pnp. And the other graphs that compare the known pnp to a calculated pnp. This graph is the first case. It is definitely logarithmic. In fact, I think it is related to the normal distribution. I show -5 to 5. Yes I know I must know x = 5 when looking at the graph. But you must admit when you plug and chug different values x, the results should be approaching x to the third. The other 3 equations in this thread still apply. They are just overly complex. The graphs of those equations still have patterns. The pattern of this graph is logarithmic. But the advantage of graphing is to find the derivative or perform other operations. The equation itself in is a pattern.
-
Simple yet interesting.
You are correct the equation is only true for zero for integers. But as you also know I am only looking for decimal approximations. An x of 5 and a pnp of 85 fall within reasonable range. I am looking for numbers for computation. The application of the cubed root of 124.9136 is close enough to the cubed root of 125.
-
Simple yet interesting.
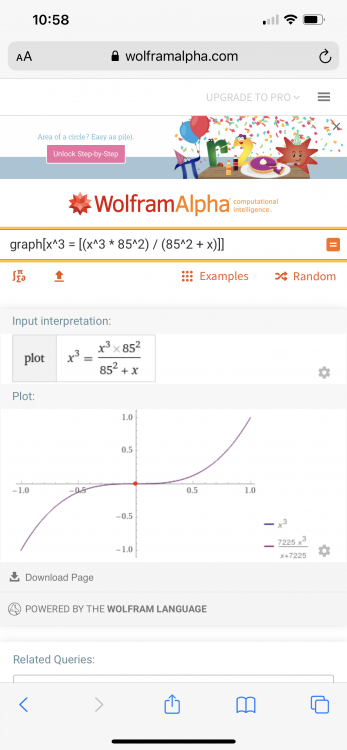
Sorry try Remember there is no guarantee it works, but it is simple enough to test. x^3 = [(x^3 * pnp^2) / (pnp^2 + x)] try pnp=85 and an x of 5 Then test more values.
-
Simple yet interesting.
Just for you Ghideon I simplified the equation to prove you do understand it. It has been said if you can’t explain it simply you don’t understand it. Remember there is no guarantee it works, but it is simple enough to test. x^3 = [(x^2 * pnp^2) / (pnp^2 + x)] try pnp=85 and an x of 5 Then test more values. Again it may not work but you have followed my thread and challenged me to simplify and prove my hypothesis.
-
Simple yet interesting.
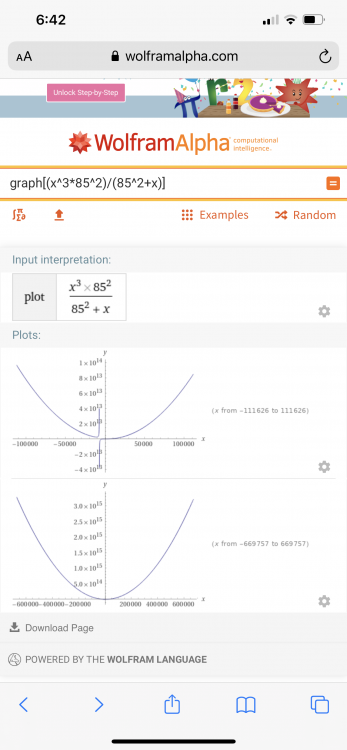
“Remember I am claiming I can factor semi-Primes and thus RSA cryptography would be no more.” This comment is to create interest. It is why we are finding semiprime factors in the first place. If I could factor semiprimes with the Pappy Craylar method it would break RSA cryptography. RSA is the first public key crypto. There is no longer prizes for cracking it hence the Pappy Craylar method is shared here. “Yes. And my understanding of the is that you try the opposite; predicting the person from too few polygons. Crude example: There is a pattern, all my models has one polygon. But that is not enough to find the unknown person below.” I should clarify that I am not finding the persons volume, I am referring to the person’s shape, the actual drawing. “I would like some explanation of, or reference to, the mathematical principles that you believe could predict the factors of a large semi prime when the factors are random.” x = Sqrt[ [ ((x^2 * pnp^4 + 2 * pnp^2 * x^5) + x^8) / pnp^4]] x - Sqrt[ [ ((x^2 * pnp^4 + 2 * pnp^2 * x^5) + x^8) / pnp^4]] = 0 Graph for x=0 to pnp; where y = 0 is your x, where x > 0 There are no tricks. I welcome the questions. I think I have something. But you never know with math. BTW if you can solve for x=0 without plotting it, it’s groundbreaking. And the graph of what you just plotted shows a pattern.
-
Simple yet interesting.
“I know where you claim the pattern to be. I want to know how there could be a pattern.” How could there not be a pattern? How is there a pattern in DNA with billions of proteins? It is just a model to better understand relationships. Do patterns exist or do you create them? Graphing the equation for possible x’s for given semi prime should show a pattern of x. A scatter plot may or may not show a pattern. But most things that are described by equations is a first step in finding patterns, especially when they are graphed. The graph of the logarithmic spiral is separate from the 4 equations. It is in polar coordinates. The logarithmic spiral could fail if the areas did not fit logarithmically with different Prime factors. But if you graphed the same Prime number with all possible Prime numbers a pattern may result:3*3 3*5 3*7 3*11 The reason I believe there is a pattern is from the log spiral model. Most attempts to find patterns in Primes is solving series. I used geometry and equations. I was a graphic artist. They teach that when you draw something it helps to break the scene into basic shapes. Obviously the world is chaotic but if you were to 3D model a person you would break them into polygons. And yes, I believe there are patterns in everything. If there weren’t we would not have mathematicians.
-
Simple yet interesting.
Sorry for the delay. I was on a trip. Well my goal is to convince you a pattern exists. The scatter plot does not show a pattern, but that is true of many patterns. Although some one YouTube did show that Prime numbers in the coordinate plane fits a logarithmic spiral. It is different from my work but I say the 4 equations show the pattern. If you graph the equation for one Prime number and a domain of possibly x values, it is an inverted normal distribution. The pattern is in the equations. Without that pattern we have no pattern. So if you do not see a pattern in the equations there is no pattern. The log spiral is separate from the equations. It uses areas. I am working on the drawing. No guarantee it will work, but I just want to show my logic.
-
Simple yet interesting.
There is a chance my spiral may “break the rules” of a log spiral. If so it doesn’t matter it would just be a custom spiral. I need to draw it. From here on out I will call this project the Pappy Craylar Conjecture.
-
Simple yet interesting.
Yes a semi-Prime based on two random Primes. I refer you to the four equations already in this thread. Plug and chug. I know plug and chug is referred to as improper math, but here we are just testing values. I know I can’t yet find x perfectly. But the equations show the pattern between the semi-Prime and the smaller factor x. I know you are think so what if we know PNP and x we know y. Point taken. But you can test for x by graphing the equation. Which I am arguing is faster then recursive division. The pattern I am trying to draw on the log spiral is from the four equations. The equations do not hold true for non-semi-Primes. So I figure if I can come up with a geometric model of the equations a pattern may result in the model. I need to draw the log spiral, I know. My hypothesis was that if I could relate the area of the sector to the semi-Prime at arc lengths of the Prime products a pattern would result. That is because the equations are only true for Prime products. I know, I should draw the log spiral and prove it. But to do so is very labor intensive, so I though I get feedback on the forum. The link WTF posted had beautiful graphics but it was just a sieve. I don’t know how to program my log spiral. It should be possible but it is very complex. Hopes this helps explain my reasoning. Plug and chug the equations. That should show the pattern in factors. A pattern unique to semi-Primes. It really isn’t a pattern of Primes put a pattern in factoring. Like in science where you can’t find answers directly, instead you use what’s known and find the pattern indirectly.
-
Simple yet interesting.
Awesome link. I wonder what they used to create the graphics. That is different from my attempts. They just have a sieve. I am trying to find a log spiral where the area equals the Prime products. The area should not equal with numbers that aren’t Prime. The parabola I created isn’t a sieve. That is why I asked you to look at the worked example. I tried to write a mathematical proof. I enjoyed the link. I have never seen other people relating Primes to parabolas. It seems like just a sieve and it is very complex. I know my looks complex like any factors will work with any number but it should only work with Prime products.
-
Simple yet interesting.
Clarity and argument are good. I post to solve problems and have good discussion. I envisioned the log spiral to increase in magnitude. The magnitude being the arc of Prime factors, 5 and 17. I propose as the magnitude increases so does the log spiral and it’s sector. That is given. But what if we graph 3*5 then graph 5*7 then 7*11 then 11*13? Will we find relations between their angles and areas of the sector. I don’t know of any attempts to do this.But other the circular functions and a spiral I don’t know where this idea could be tested geometrically If you took 3*5 then 3*7 then 3*11 ... then 3*5 then 5*7 then 5*11... and graphed them on a log spiral at the very least it would organize the Primes. But what if you tried a number that wasn’t a Semi-Prime would the area match the product of the 2 products that form the radius? Does the log spiral formed by 5*17=85 fit all Semi-Primes? Can we mathematically change the spiral so that we can test manipulations like a sine curve for alternating current? Can we find patterns in factors only seen in Semi-Primes: (x^3/N) approximately= (x^2/y) Here you could invert the fractions and see if the area between x and y, N is divisible by x^3 as y is divisible by x^2 There are other tests such as: (25/17) approximately= (85/58) That is my argument of the log spirals usefulness.
-
Simple yet interesting.
Well that is completely unscientific. You did not prove it wrong. You took one value and came to the conclusion it has nothing to do with Semi-Primes even though you just took 2 factors and related the sector area to the Semi-Prime. So simple that it seems insignificant. But the hypothesis exists to disprove. You have to creat an algorithm to graph all known Semi-Primes or at least enough to sample the data. If you believe that any of the 4 equations I posted show any pattern in the factoring of Semi-Primes, why would you think this geometric model would not have any truth?
-
Simple yet interesting.
A=r(φ2)2−r(φ1)2 /4K But you didn’t use the area equation right. Radius * angle squared - radius * angle squared divided by 4K
-
Simple yet interesting.
The parable work was posted June 9th. I propose there will be a pattern once we do this process with all possible SemiPrimes. If no pattern we can still manipulate the semiPrimes as we would a log spiral.
-
Simple yet interesting.
I mean from the origin to a radius of 17 the angle between is 62 degrees. How did you square 17 and 5 without taking into account the angle between each. I think you missed a variable The angle is the unknown. My answer may be wrong. I will write it up when I get a chance. But I also think you forgot the angles in the area equation. No, it ties in differently. I want you to also comment on that worked example but we are on log spiral now.
-
Simple yet interesting.
I got an angle between zero and 17 of 62.14599 degrees. Is that what you got? BTW, what are the errors of the 2sided triangle worked example I posted in the pictures. I wrote it 12 years ago. If it can be corrected, it would be useful. You should note it is inside a parabola. It is probably flawed but my description seems like a worthy effort. I just gave you the angle now because I don’t have time to write out my work now.
-
Simple yet interesting.
No, it is untested as I said. I was just showing the example I was describing. I think it should be solved by the equation of area of sector. Else it is difficult to draw. I was looking to draw it in AutoCAD 14 or FreeCad. But if it is done by equations first it would be possible to draw relatively easy. Remember it only my hypothesis. But it is also the model I based all my work on. The process is simple: relate the math work to geometry. But starting a pattern in the geometry is challenging. I believe if we can make the geometry represent the equation, patterns will result. Patterns that couldn’t be found looking at the equation alone. Do you have any drawing software to recommend? Also incase you didn’t know I am developing my hypothesis in real time. I have done that since I started working on it. The 4 equations I posted have been developed for some time, but the hypothesis are being done in real time.
-
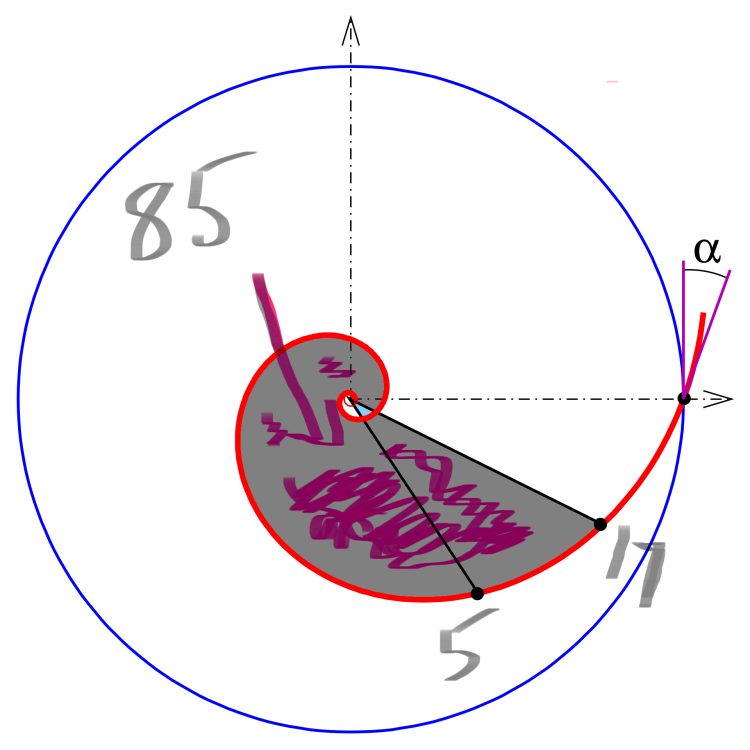
Simple yet interesting.
I still need to test using equation, but a log spiral with a radius from 5 to 17 and a sector area of 85. Just have to plug and chug into equation to be sure an area of 85 can be reached Excuse the graphic. It is rugged but shows what I mean. I am a trained graphic artist but I face compatibility issues since most programs are subscription based. I have to change the way I design and what tools I use. If this works I will draw a triangle.
-
Simple yet interesting.
Back to the discussion. I concede using triangles to relate factors to products is challenging. This is the best I could come up with: For semi-Primes and their product where 5 * 17 = 85 a logarithmic spiral with radius 5 and 17 with the angle between 5 and 17 equal to the angle where the area of the logarithmic spiral encompasses an area of 85. You just design the spiral using the known 5, 17, and 85. Do you see any advantage to doing this? I am working on a worked example. The reasons I think it is useful is that it is simple, includes all 3 values, is reproducible, and properties of log spirals are already known. I envision a logarithmic spiral that has semi-Primes positioned along similar angles that occur at different magnitudes. That is similar angles reaching to different lengths of the logarithmic spiral.
-
Simple yet interesting.
I Ok. You wanted a worked example. This is for “crafting” a triangle. There is a high probability it doesn’t work. But I wrote it in 2009 and am trying to relearn my reasoning. This isn’t the “vector factors” I talked about. But it is a geometric representation of algebra. It is what is in the pdf I posted but you probably haven’t seen it. It is based in a parabola. I just want to know if it works. No one has ever tested it. I know it might appear absurd but I was inspired when I wrote it. I will address the current discussion in a future post. It is difficult to relate vectors to factors. But I still think it be useful to create such a model. Refer to the images for crafting triangles.