Trurl

There are still problems. s does not equal N/Pi but angle AFC should. That is if the triangles are similar. The only place that the sides of the triangle should be an integer is at x and y. AFC = (remainder(N/Pi)) * Pi (In theory)

Ok, sorry I haven’t replied sooner. I have changed that s is now the remainder of N/Pi. That is a 180 the max angle (straight line). I did this because I couldn’t remember the modulus definition. I am saying that if N is much larger than x and y the Prime factors that x would wrap around the half circle (180 degrees) N/Pi times. The remainder would form a triangle where x and y would add to find the remainder of N/Pi as the similar triangle AFC. So triangle AFC is similar to triangle xys. (Yes I know the label isn’t standard.) Why did I do this? There is no guarantee this will make the solution simpler. But I already have proven equations for x and y as related in terms of x and N. I was going to use these equations and place them to the sides of the triangle and use the equations we know about triangles to solve for a pattern. This is a long shot, but I have always pictured the Prime factorization as a logarithmic spiral. That is why I wrapped x at an angle around the circle. I realize this theory has somehow gotten away from me. It is extremely confusing. But I stand behind my underlying theory. As you read my earlier post on this thread, I have found patterns in the Prime factorization. The resulting equations are just impossible to solve to be useful. I thought since I cannot solve the polynomial equation, I would make a graphical representation, but I need to reevaluate this. Perhaps if I map out the entire idea, you guys could assist me in making it makes sense. I am have been busy and it takes time but I think I should explain more, even though this post is an attempt to explain. But in the coming weeks I will work on this. Try not to laugh at me too much.

OK, first off I’m sorry l haven’t replied sooner, but I have been busy. Second, I think you guys overestimate my knowledge of biology and genetics. I want to look for patterns in the genetic code. I have did a little research and I don’t know what the information needs. I need a starting point. You guys gave me excellent information. But I cannot test the DNA myself. I have an upper-level chemistry book that says to place a specimen in a spectrophotometer. I have googled it and it is affordable. My chemistry book does not list steps however. It has theory then puts a list of 7 steps on what to do without a complete lab explanation. I should explain more what I want to do. I want to look for patterns in genetics. As you guys stated that a lot of information is shared. I think it is like a networked science where the public looks at the data, like finding constellations in telescope pictures. I’m not claiming to be able to discover anything. I have tried to find patterns on the Prime factorization problem. I have found some patterns, but I don’t have a solution to the problem. As you can see from my math post on SFN. So I suppose my question is can I do any meaningful experiments. And by meaningful I mean worth the price of a $500 spectrophotometer to do amateur experiments and have some fun. I also have a question of the value of my own DNA. I was thinking of doing the Ancestry.com DNA test. But if I give my DNA do I compromise my privacy? I have DNA on record from being in the military. The military has a great DNA base of every member since approximately 1996. They are only supposed to use the DNA for identification, but imagine the information they collect on everyone with both nature vs. nurture. But I imagine a world where cryptography and identity will utilize the genetic information. Is it safe to give Ancestry.com genetic fingerprint? BTW, when I was talking about God, it was not in a religious way. I was asking does a one-way function exist. If an all-powerful being can create a function can they reverse it? If they can there are no one-way functions. But if the being can’t reverse it, one-way functions exist. Either way some would say that either would mean they are not all knowing. The boulder problem is a non-religious person’s argument. But I mention this only as the meaning of a one-way function. It is not intended to prove any religious viewpoint right or wrong. It is just a conundrum.

https://1drv.ms/i/s!Ao7PhUWlkaBthGPYxf06XrWnNzKL Definitely some problems with my geometric representation. Does this look better?

Ok, for my background I am a college student. I confess to not knowing biology or genetics or even engineering for that matter. I have read some books on genetics and I am particularly interested in gene-therapy. But I have read that genetics is related in many ways to cryptography. I have tried here at SFN in a math post to solve the Prime-product problem. I have had little success so far. I have a polynomial which if you already know the Prime numbers proves true, but by itself I cannot solve the resulting equation. I have tried geometry and am currently looking at other methods. My question is how do you read the genetic code chemically? I have seen some basic experiments in a Make biology book. Also what are the cytological algorithms? From my brief research the math problem is complex and differs from gene pattern to pattern. So not only do you have to solve a genealogic one-way-function, but you don’t know the algorithm that pattern is based on. And most gene knowledge is not shared due to the fact it is a big-money intellectual property. So with most researchers working alone it is no wonder mathematicians haven’t solved it. My approach is to find a pattern that not only describes the RSA Key algorithm, but will find patterns where patterns don’t seem to exist. I believe in creation, but will not preach but list this to note something very important. A nonbeliever asked if God is so powerful can He make a bolder so heavy even he can’t lift. This sounds ignorant. The nonbeliever would say he isn’t all powerful if he can’t lift the bolder and if he can’t lift hit he can’t lift the heaviest boulder. I know it sounds like nonsense. But my question is can God make a function that cannot be reversed? Obviously I don’t know what God is capable of. There are easily one-way functions we cannot reverse. However I don’t see genetics as something that can’t be figured out. Some scientist, see genetics as chemical proof God does not exist. I believe the pattern just shows his work. The fact remains that knowledge of genetics is as dangerous as the fruit from the Tree of Life. That is just my perspective. I don’t want to argue if genetics proves we evolved. I am just stating why I am interested in genetics. I want to find patterns in them. Obviously I am limited in what I can do. I don’t have a lab or biology background. But I found this article which described a one-way biological function. Also you should check out my post in the math forum. Please share if you know any simple genetic experiments. I have the catalog of American Scientific’s “Amateur Scientist” columns. I have a professional microscope, power tools, Internet, cryptography books, and an impossible to solve polynomial. I’m not intending to cure cancer, but I want to look at patterns in DNA that could relate to cryptography. http://www.asee.org/documents/sections/middle-atlantic/fall-2009/01-Biological-One-way-Functions.pdf http://www.scienceforums.net/topic/95813-prime-products-just-one-last-time/

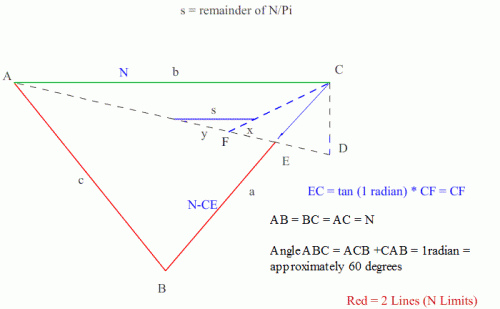
Imatfaal, I am not arguing that 60 deg = 1 radian. 1 rad is 180/Pi. I am only looking to find a symbolic value of angle AFC. The entire point of drawing the triangle with side N is to find angle AFC. As for degrees, it would be fine to find angle AFC in degrees. The question is can anyone symbolically find this angle. If you can I will tell you why I want to know its equation for.

https://1drv.ms/i/s!Ao7PhUWlkaBthFy7UgDHUGEIh2Lm Here is my updated drawing. It could still be wrong. I may have some flawed logic. But I am seeing this idea develop, but I cannot explain it. It is abstract. I know if I write it out and keep it as simple as possible, maybe someone else will be able to see it also. That is what I hope. Let me know what you think. This is only the start of the problem. But I need some input that the vector addition with sides x and y (the 2 Prime numbers multiplied together with an angle between them (the angle approaches the limit of Pi radians) have a resultant of N (where N is the product of the 2 Prime numbers x and y). Let me know if this conveys anything. An idea is not as valuable when no one else can understand what you are trying to do.

Very interesting. The question to answer is how it differs from a regular gear. Inter-locking the forces on the gear could be distributed differently. I am not sure of the inter-locking would allow circular motion. They would be in conflict during rotation. However don't be deterred. If certain Pokadoves were stationary while others rotated as a gear you could produce custom orbits. That is irregular non-circulat orbits. Think unsemetric objects like a space station. This is good work. I'm just giving my opinion. I am no authority on the subject. But you need to research gears in a machine design book. Again cool shape; creative design; I'm just not sure how it moves. Are you suggesting to use it as a mag wheel? Or is it to inter-lock as a tool?

Yes, my drawing and explanation are off. But don’t disregard the idea yet. This is a one of the graphical representations of my algebraic work posted earlier in this post. Things to remember when looking at this drawing: This is a vector. Both x and y are Prime numbers We are looking for the smallest lengths x and y possible. (They represent Prime numbers after all. There are no angle sides multiples of x and y. Again, these are prime factors. So, there is no 2x or 2y or 3x and 3y. As the lengths of x and y increase, the angle between them decreases. This is significant because the vector addition of x and y is less than N. And for my solution x < y. sin(60 degrees) = 0.866025404 sin(1 radian) = 0.841470985 cos(60 degrees) = 0.5 cos(1 radian) = 0.540302306 This relates to the same error of my equations. I am working on this problem off and on. I will try and produce a better and corrected drawing.

Ok, my last post wasn’t very clear. Here is what I was trying to do. N is known. x and y the 2 number that when multiplied together make N. I am trying to simplify the factoring by using a simple vector. This vector might be able to be solved to find the unknown factors x and y. Picture an angle between 2 lines. As the lines increase in distance so the angle stays the same, but the distance between the 2 lines also increases. So I start with a triangle whose segment opposite the (obtuse) angle between the lines equals N. Now I take this same length N and travel along the original 2 lines until the length along the lines approaches a segment between those lines as N. N is the point where the segment between the 2 lines will reach the limit of N. Beyond N the segment is bigger than N. This is where I need your help. Just to see if this is worth pursuing. The other limit (opposite end of the N segment) is 1 Radian with a radius of N. So, on a circle with radius N with 2 sides N and the angle between 1 Radian. I am not sure as you pointed out the triangle of 60 degrees is not 1 radian. But I am referring to the relative angle between side N and side N. So, the tangent of x equals N -x. N is known This is the tricky part! I have not solved this yet. But I am saying I could possibly use the equations I found a pattern in the Prime factors. Which until know is too complex. But Knowing N and the angle opposite N… I am saying there is a possibility of substituting the equations for x with a new simpler equation of x in this geometry. I am not claiming this works. It was just something I was thinking about. Remember this drawing is off. I need to make a clearer drawing. https://1drv.ms/f/s!Ao7PhUWlkaBtgQd7IjIjxkBjv3wz

I am going to keep this short, because it is just an idea I was working on and I have school work to do and not silly math ideas. But imagine a circle where N is the product of 2 Prime numbers. The radius of the circle is N, so in 1 radian a triangle is formed with a segment opposite the 1 radian angle is N. So an equilateral triangle is formed with all sides equaling N. But we want to know the angle of a triangle with the side opposite the obtuse angle is also of length N, but we have lengths "x" and "y" that are unknown sides. Could we take the N-equilateral triangle and subtract x from one of the end sides? The theory is that the y side would complete the triangle giving us the obtuse's angle in form of an equation with variables in N and x. Can anyone disprove that this will not geometrically solve an unknown triangle of one side N, which is known, and put into equation form x and y? I will add more to this when I have time. I can't insert the picture so it is difficult to visualize what I am describing. I know it sounds stupid, but there is some thought here. Let me know what you think. Trurl

Thanks for the link. The following is why I started researching this idea. It may seem silly but does anyone get anything from this? I'm not sure if anyone got anything from the previous posts but this is going to sound brilliant or a bunch of malarkey. Let me start by saying that this idea is just a theory and nothing is proven. This is just an example of how I approach a math problem. It is very much intuitive and visual. The idea: PNP is given and the unit circle will be used to find x and y. (These variables correspond to my previous equations.) The area encompassed by the angles on the unit circle will be used to form equations that find the values of x and y. Imagine a vector solved by the method of parallelogram addition. That is there is a triangle with 2 known sides x and y. Through vector addition and an angle of y/x radians between the sides the area can be found. This area is theoretically equivalent to N in value. The problem is N is the only value we know. To be useful we have to know y/x are at least some properties and proportions. We cannot use vector addition directly because N is only given. But it may be useful to use the unit circle to find which x and y will equal N. So a circle with radius x and a y arc length from an angle of y/x radians, has an area encompassed by the unit circle equal to N. This encompassed area is of angle y/x. If y/x is larger than 2Pi*x the angle encompasses one or more of the circle. That is the idea. I don’t know if it works, but it is how I go about math problems. This would relate to my theory of a logarithmic spiral that would show a pattern in the placement of Prime numbers. I have had this idea for quite some time. As seen in these URL’s: http://www.constructorscorner.net/ideas_and_gadgets/math/math_hunch/hunch_00001/hunches_section0005/trig_parabola.html http://www.constructorscorner.net/ideas_and_gadgets/math/math_hunch/hunch_00001/hunches_section0005/trig_parabola_verified.html http://www.constructorscorner.net/ideas_and_gadgets/math/math_hunch/hunch_00001/hunches_section0008/PrimeRevolutions.html If it is true this is just one step. There must be a way to solve the unknowns x and y in equation form. Remember PNP/y equals a distance of 1 radian. And remember this is only a preliminary idea I want input on. I am not clamming it works. I just think it is interesting enough to consider. Trurl [bJS1]

I don't know the speed. But Mathematica can draw graphs fast. I am looking for some guidance on how to program numbers of hundreds of digits. See for yourself on the code and attachments that these 2 equations work with large values. So if you agree or disagree just post here. I am researching ways to use calculus on the graphs and also have other methods of solving the polynomials. Here is my results of my last effort that has changed from finding patterns in Prime multiplication to solving the found polynomial equations. In[32]:= PNP = 7727* 65537 t = 7727 Sqrt[(((((t^2*PNP^4 + 2*PNP^2 * t^5) + t^8)/ PNP^4 ) - ((1 - t^2/(2*PNP)))) * ((PNP^2/t^2 ))) ] t * ( ((PNP^4/t + 2* (PNP^2 *t^2) + t^5) / PNP^3) - 2*(t^2/PNP) ) Out[32]= 506404399 Out[33]= 7727 Out[34]= (11 Sqrt[18205987286897013994227797/2])/65537 In[36]:= N[(11 Sqrt[18205987286897013994227797/2])/65537, 14] Out[36]= 5.0640530604466*10^8 Out[30]= 142546691485720530013630/281487861809153 In[31]:= N[142546691485720530013630/281487861809153] Out[31]= 5.06404*10^8 SFN_PatternsPDFHigherValues.pdf SFN_PatternsPDFHigherValuesb.pdf

I have attached a PDF of graphs. PlotofUglyEquationsV8_20160704.pdf

Did anyone agree or disagree with my last post? Obviously the odds are against breaking a one way function. But if you feel it doesn’t work please be my guest to call me stupid. Shooting an idea down is better than no response at all. I am serious in my attempts and have other equations or patterns in products. I also need guidance on how to program numbers. I mean recursive factoring. Traditionally large numbers are difficult to program. Mathematica can handle about 300 digits. So proceed to disprove this problem if you decide it needs bashing. Here is another pattern that I believe to be unique of Prime Products. It is simpler than the last, but still complex to solve the polynomial. Many of the equations or patterns as I call them are true for all x and y. However there are some (though complex) patterns are only true to Prime factors as shown below. There are several with one from the last work to this one giving us 2 complicated but true patterns. y = ((PNP^4/x + 2* (PNP^2 * x^2) + x^5) / PNP^3) I believe this equation to be a pattern of multiplication to solve for a y that is unique, that is it doesn't prove always true with all x's. x * y = PNP x * ((PNP^4/x + 2* (PNP^2 * x^2) + x^5) / PNP^3) = PNP or another equation y = y ((PNP^4/x + 2* (PNP^2 * x^2) + x^5) / PNP^3) == PNP/x I will continue to find errors in my equations and post those that are unique to Prime factors. Maybe a simpler mathematical equation can be found. With error : x * ( ((PNP^4/x + 2* (PNP^2 * x^2) + x^5) / PNP^3) - 2*(x^2/PNP) ) = PNP

I do not disagree. I do not have a way to mathematically solve this complex and ugly polynomial. What I am saying is y has been eliminated from the equation. When you graph 85/x to find y both x and y are unknown. The quotient leaves no clue as to what values you are looking for. When you graph the ugly left side of my equation x is still trial and error, but you are looking on the graph for 85^2 (or 85 if you graph the square root of the equation). The graph is a one to one and y increases as x increases. So when an x of 3 is 80 and x of 7 is 88 the x that is 85 is between them. I prose using statics (calculus) to find the properties of the graph. There isn't an advantage for an PNP of 85 but a large factor where factoring is difficult my method may prove useful. But I do not how to program million digit numbers. But do you agree if you use trail and error, you are approaching the known PNP and at least know that your x is larger or smaller than the x which is the factor? That is something division alone does not show.

Wait a minute I decided it was simple logic. In your pen and paper your division does not show how close the calculation was to the correct factor. We know we are aiming for 85. This method shows 3 is below 85 and 7 is above. Do you still think there is no pattern?

I know the equation is ugly. But what if such an equation existed how should it look? I think the one advantage of my method is that it can be graphed. I know that division is faster but I see advantages when working with larger numbers. In your pen and paper estimates you know what to try but my method but mine is static in that it shows how far the tested number is from 85. Yes this has to be proved. This is the reason I share this post. Of course this probably proves wrong. But sometimes you get gold fever and go looking for gold dust.

PNP = 85 x = 3 (((((x^2*PNP^4 + 2*PNP^2 * x^5) + x^8)/ PNP^4 ) - ((1 - x^2/(2*PNP)))) * ((PNP^2/x^2 ))) 85 3 847772947/130050 N[847772947/130050, 14] 6518.8231218762 Sqrt[6518.82312187620146097654748173779315647828`14.] 80.739229138481 In[1]:= PNP = 85 x = 7 (((((x^2*PNP^4 + 2*PNP^2 * x^5) + x^8)/ PNP^4 ) - ((1 - x^2/(2*PNP)))) * ((PNP^2/x^2 ))) Out[1]= 85 Out[2]= 7 Out[3]= 5538604027/708050 In[5]:= N[5538604027/708050, 14] Out[5]= 7822.3346190241 In[6]:= Sqrt[7822.33461902408022032342348704187557375892`14.] Out[6]= 88.443963157607 These values do not produce an N of 85. That is, we know the value of N. It is what was eliminated from the right side of the equation. So it is a significant value that is produced by the left hand side of the equation. 3 is 80.7 and 7 is 88.4 so the Prime number with the value closest to 85 (within a fraction of error) is 5. Note the sides of the main equaiton are already squared in form. I did this to remove the square root. The values fo the equation reflect this. A computer program could be written to test values based on the results of the left hand side of the equaiton. I know it isn't a perfect math solutions where I solved the polynomial but there is a distinction in the numbers. It tells the user if the number that was tested was too large or too small. I will address more quesitons in a future post. In[7]:= PNP = 85 x = 5 (((((x^2*PNP^4 + 2*PNP^2 * x^5) + x^8)/ PNP^4 ) - ((1 - x^2/(2*PNP)))) * ((PNP^2/x^2 ))) Out[7]= 85 Out[8]= 5 Out[9]= 4179323/578 In[10]:= N[4179323/578, 14] In[11]:= 7230.66262975778546712802768166089965397924`14. Sqrt[7230.66262975778546712802768166089965397924`14.] Out[11]= 7230.6626297578 Out[12]= 85.033303062728

The equation is simply: x^2 * y^2 = PNP^2 Which stands for: p^2 * q^2 = N^2 The left side of the equation is x and y. (They are multiplied together to get PNP.) The right side is PNP. Both sides squared of course. I cannot solve this polynomial equation. If I could I would know instantly what x is. However if values are tested starting with smaller Prime numbers, ( x is the smaller product), I believe you will have a feel for where x is because the equation with x plugged in will be approaching PNP (85 in this example). I believe you could statistically use trial and error to find x. (As PNP approaches 85, x approaches 5.) You could change the equations to find y instead of x and use both the y and x versions to statistically eliminate products. The question is does it work. I am not so much concerned with speed. I do not know how to program million digit numbers. But I think the larger the product the more valuable a statistically found solution is. Of course if I could solve the polynomial (Which I can’t now, but I still have a few more tricks in my mathematical tool chest.) the problem would be solved. However I don’t claim this solution to be faster, but it represents a different approach. I do however value feedback. Most people say this is stupid. I agree that the problem is impossible. I just had an idea for a different spin on it. I could use already discovered methods of evaluation, but other than the math lesson that would provide wouldn’t it just be doing the same thing and expecting different results. I approach this as a learning exercise. I have read much about cryptography and Mathematica. In short if it’s wrong, it’s wrong. The only reason I put so much work into it is because I of my first idea that a logarithmic spiral could find a pattern in Prime numbers and maybe other sorts of patterns that seem to have no pattern. So that is what I am trying to do. The only thing that would increase the speed of this equation would be a statistical (calculus) evaluation. If you test for x and it doesn’t equal PNP then you know if it is larger or smaller. Then you test again knowing that when x gets bigger, y gets smaller. So instead of making unlimited processes you can make an educated guess.

Ok I wanted to see if this idea had any potential and I figured if it didn’t it would be shot down in a matter of minutes. This is my final work on the Prime product problem. I know it is just x^2 * y^2 = PNP^2 However the terms would just cancel out. Instead I have decided to let x^2 equal a pattern of x and PNP. So I just substituted the equation which is more complex and will not equal the right side of the equation for x^2. In calculus where you have a complex derivative where you let du/dx equal a portion of the derivative so you can understand and simplify the manipulation of the integral. I am instead taking a more complex pattern and leaving it so x^2 does not cancel x squared. By doing this I hope it solves the pattern. So if you could solve this polynomial equation you would solve the factorization problem. If you couldn’t solve the polynomial? Well you could just write an algorithm that plugged in Prime numbers from smallest to largest. And because the polynomial is set up to find PNP you would get a feel for the range x was in. I mean, that this time when you try a number how far away the computed value is from PNP is significant. So if this works it is faster than using division to factor. But of course I await any disagreeing opinions. I now this problem gets that. But it was my final attempt before moving on to a different problem to pursue. (((((x^2*PNP^4 + 2*PNP^2 * x^5) + x^8)/ PNP^4 ) - ((1 - x^2/(2*PNP)))) * ((PNP^2/x^2 ))) == PNP^2 Above is the pattern of x^2 * y^2 = PNP^2 It is not to be simplified yet x put and tested in that place. It is faster than division since the equation approaches PNP as the proper x is used. Smallest to largest Prime numbers are to be used. PNP = 85 x = 5 (((((x^2*PNP^4 + 2*PNP^2 * x^5) + x^8)/ PNP^4 ) - ((1 - x^2/(2*PNP)))) * ((PNP^2/x^2 ))) 85 5 4179323/578 N[4179323/578, 14] Sqrt[7230.66262975778546712802768166089965397924`14.] 85.033303062728 ((((x^2*PNP^4 + 2*PNP^2 * x^5) + x^8)/ PNP^4 ) - ((1 - x^2/(2*PNP)))) 4179323/167042 N[4179323/167042, 14] 25.019593874594 ((PNP^2/x^2)) 289 Questions to ask: Is it unique to factors of PNP or does it just give a decimal to all real numbers? Does it work for other values of PNP and x? Is it faster than factoring (recursion)?. Is it just x = x and as so not a useful pattern? Can the error be programmed? Verify then post. That is what I need to do. But I actually believe there is a pattern here. The question is does it work for all PNP and x values. I have many patterns. Some answer some of the questions. But I haven't found a polynomial I can solve after these questions have been answered. For example if this worked, I would need to solve the given equation. And this proves to be challenging. PNP = 85 x = 3 (((((x^2*PNP^4 + 2*PNP^2 * x^5) + x^8)/ PNP^4 ) - ((1 - x^2/(2*PNP)))) * ((PNP^2/x^2 ))) 85 3 847772947/130050 N[847772947/130050, 14] 6518.8231218762 Sqrt[6518.8231218762] 80.739229138481

More equations. More evidence of patterns. Can such a polynomial be solved and can it be done by hand? Here are more examples. That is values being tested. There is my signiture PNP = 85 and x = 5. As you can see y = y again. And there is more distrinction between possible Prime products at different values. Here I square both sides and y no longer equals y until we take the square root of the answers. Again y = y with distinction in the Prime factors, but it would take a computer algorithm to find x. I cannot use the NSolve command in Mathematica and get accurate results. How do I go about solving such a polynomial? In[82]:= PNP = 85 x = 5 ((PNP^4/x + (2* (PNP^2 * x^2) + x^5))/ PNP^3) (PNP * PNP/x - x^2)/ x Out[82]= 85 Out[83]= 5 Out[84]= 86436/4913 Out[85]= 284 In[81]:= N[86436/4913] In[86]:= 17.593323834724202` Sqrt (284) Out[86]= 17.5933 284 Sqrt Below I try NSolve. Even though the equations are algebr In[89]:= PNP = 85 NSolve[(((PNP^4/x + (2* (PNP^2 * x^2) + x^5))/ PNP^3))^2 == (PNP * PNP/x - x^2)/ x, x] Out[89]= 85 Out[90]= {} Below I squared both sides to elminate the square root. Did not help, but I do have equations where I have eliminated it. Again how to I go about simplifying and solving these polynomial equations by hand? In[102]:= PNP = 85 x = 5 (((PNP^4/x + (2* (PNP^2 * x^2) + x^5))/ PNP^3))^2 (PNP * PNP/x - x^2)/ x Out[102]= 85 Out[103]= 5 Out[104]= 7471182096/24137569 In[106]:= N[7471182096/24137569, 20] Out[106]= 309.52504355347466847 In[107]:= Sqrt (309.52504355347466847220612813162750565312`20.) Out[107]= 309.52504355347466847 Sqrt 284 I like the square root here. It is showing that increments in y signify small changes in x. It also seems to help with small value changes in value of x. For example x =3 value significantly deferes from x = 5. This is more evident in larger numbers. In[117]:= PNP = 85 x = 3 (((PNP^4/x + (2* (PNP^2 * x^2) + x^5))/ PNP^3))^2 (PNP * PNP/x - x^2)/ x Out[117]= 85 Out[118]= 3 Out[119]= 2765866292982016/3394345640625 In[121]:= N[2765866292982016/3394345640625] Out[121]= 814.845 These may not seem spetacular. But there are important relationships here. Look at the numbers and the results of testing knowing both PNP and x. It is not simple plug and chug. The question is if the polynomial can be solved.

Back to the drawing board. I will state my problem more cleary. I have had it find x knowing only N in previous tries. But this time it is wrong and I am not sure while because when you do plug in x it does seem the left and right side of the equation works. What is the error here? If discoverable? Let PNP = N ; x = p and y = q where N = p * q where N is the product of 2 Prime numbers p and q. x is the smaller Prime number. The 2 equations equal y to solve a polynomial equation where N is given Here is my best equation so far. I think that y = y (each side of equation equals y). x is unknown so solving the polynomal knowing N may work if the 2 seperate equations for y are unique to Prime factors and not true for all integers. So you see it is simple algebra except for the part of solving the polynomial. I have other equations that eliminate the square and I believe this is why Mathematica is not solving the polynomal correctly. Also Mathematica can not distinquish from 0 and 0.0007. There error of the equations because alone they are off by an error of (x^2 / x) and (x^2/ (2*PNP) respectively. As the error becomes closer there may be more numbers y = y is true. However the error is a problem and is why the solution would have to be programmed into a algorithm that can determine the value of x. I realize this is not a perfect algebraic solution. However I think that as N increases in value the accuracy also increases. Shown below is the main equation. As you can see Mathematica is not finding the proper x even though each equation, within reasonable error, is y = y. This is where I need help. I am not trained as a mathematician. I do not know how to solve this polynomial without the help of Mathematica. But do you agree that these equations equal? I know it seems impossible to break the one way function. And this proves its strength. But I still feel there is potential here. The equations following show different values of the y part of the equation knowing both N and x. (Yes I realize the equation is not useful already knowing both PNP and x. However it is just to demonstrate the values and patterns of the equations. PNP = 85 NSolve[(PNP^4/x + 2*(PNP^2*x^2) + x^5)/ PNP^3 - (2* x^2 / PNP) == (Sqrt[((PNP * (PNP/x) - x^2))/x] + (x^2/ (2*PNP))), x] 85 {{x -> -17.7913 + 13.1603 I}, {x -> -17.7913 - 13.1603 I}} In[7]:= PNP = 85 x = 5 (Sqrt[((PNP * (PNP/x) - x^2))/x] + (x^2/ (2*PNP))) (PNP^4/x + 2*(PNP^2*x^2) + x^5)/PNP^3 - (2* x^2 / PNP) Out[7]= 85 Out[8]= 5 Out[9]= 5/34 + 2 Sqrt[71] In[11]:= N[5/34 + 2 Sqrt[71]] Out[11]= 16.9994 Out[6]= 83546/4913 In[12]:= N[83546/4913] Out[12]= 17.0051 The above is where x = 5. However x =3 would also be within reasonable error. 7 and 11 also may be close. However there is still a significance of the Prime factors which should increase in distance as PNP (or N) increases in value. I could show more values, but it may complicate the presentation of the problem. In[23]:= PNP = 6911 * 4129 x = 4129 (Sqrt[((PNP * (PNP/x) - x^2))/x] + (x^2/ (2*PNP))) (PNP^4/x + 2*(PNP^2*x^2) + x^5)/PNP^3 - (2* x^2 / PNP) Out[23]= 28535519 4129 Out[25]= 4129/13822 + 4 Sqrt[2984862] In[27]:= N[4129/13822 + 4 Sqrt[2984862], 20] Out[27]= 6910.9999935435190680 Out[21]= 2281201114658882/330082636031 In[22]:= N[2281201114658882/330082636031, 20] Out[22]= 6911.0000516496147904 As seen above y = y. However it takes a computer to see the difference. Next we will test x = 4127. PNP = 6911 * 4129 x = 4127 (Sqrt[((PNP * (PNP/x) - x^2))/x] + (x^2/ (2*PNP))) (PNP^4/x + 2*(PNP^2*x^2) + x^5)/PNP^3 - (2* x^2 / PNP) Out[33]= 28535519 Out[34]= 4127 Out[35]= 17032129/57071038 + Sqrt[814205553002978]/4127 In[37]:= N[17032129/57071038 + Sqrt[814205553002978]/4127] Out[37]= 6914.35 Out[31]= 663045156038911226701180291010/95894079886244829190262593 In[32]:= N[663045156038911226701180291010/95894079886244829190262593, 20] 6914.34921556632278818568561229321882459748`20. So there is a computable difference between x = 4129 and x = 4123, in that y = y is becomming untrue as the value of the number increases of decreases from the value of the factor 4129. In[43]:= PNP = 6911 * 4129 x = 4123 (Sqrt[((PNP * (PNP/x) - x^2))/x] + (x^2/ (2*PNP))) (PNP^4/x + 2*(PNP^2*x^2) + x^5)/PNP^3 - (2* x^2 / PNP) Out[43]= 28535519 Out[44]= 4123 Out[45]= 16999129/57071038 + Sqrt[814205757190494]/4123 In[47]:= N[16999129/57071038 + Sqrt[814205757190494]/4123] Out[47]= 6921.06 Out[41]= 663045156010247586320631832010/95801136750905604737449157 In[42]:= N[663045156010247586320631832010/95801136750905604737449157, 20] Out[42]= 6921.0572911493124224

Without cheating I say: 655 I debated how much I should show here. I don't want to deceive anyone or not get credit for my work. But then I realized I could inspire someone or get help working towards a solution. But first I need to make sure it works. I will share the equation here. My other equations were correct, but when finding y it could not differentiate the factors being decimal or integers. So I had an elaborate equation that set y equal to y but it was always true. I have dozens of equations, but I think my original equation posted here shows a difference where y = y is unique. I could be wrong, but I keep trying because my ideas seem so intriguing to me. So take a look at this code and tell me what you think. In[1]:= PNP = 85 NSolve[(PNP^4/x + 2*(PNP^2*x^2) + x^5)/PNP^3 - (2* x^2 / PNP) == Sqrt[((PNP * (PNP/x) - x^2))/x] + 1/x, x] Out[1]= 85 Out[2]= {{x -> -18.4935 + 11.9812 I}, {x -> -18.4935 - 11.9812 I}, {x -> 7.54812 + 13.0737 I}, {x -> 7.54812 - 13.0737 I}, {x -> 5.44949}} In[3]:= PNP = 8141620173 NSolve[(PNP^4/x + 2*(PNP^2*x^2) + x^5)/PNP^3 - (2* x^2 / PNP) == Sqrt[((PNP * (PNP/x) - x^2))/x] + 1/x, x] Out[3]= 8141620173 Out[4]= {{x -> -3.87566*10^6 + 2.50985*10^6 I}, {x -> -3.87566*10^6 - 2.50985*10^6 I}, {x -> 1.55455*10^6 + 2.69255*10^6 I}, {x -> 1.55455*10^6 - 2.69255*10^6 I}, {x -> 2534.62}} In[5]:= PNP = 141620173 NSolve[(PNP^4/x + 2*(PNP^2*x^2) + x^5)/PNP^3 - (2* x^2 / PNP) == Sqrt[((PNP * (PNP/x) - x^2))/x] + 1/x, x] Out[5]= 141620173 Out[6]= {{x -> -260189. + 168496. I}, {x -> -260189. - 168496. I}, {x -> 104363. + 180762. I}, {x -> 104363. - 180762. I}, {x -> 656.727}}

What are N and p, and what is the relationship between them? Is N a number and p one of its prime factors? In your example, you know both N and p, so what are you trying to find? The N = p * q is the integer factoring problem. It is used in cryptography often to form a one way function. The difficulty of factoring a number with the products being 2 Prime numbers is difficult with extremely large numbers. There is no equation that will solve the products in polynomial time. I want to find p which here I called x without knowing q which I called y. If I could do this the factoring problem would be no more. Yes, I am aware that this doesn’t seem solvable by 2 equations. I have heard and know this. But I had an intuitive yet simple approach. I originally started by saying that a pattern in Prime numbers could be explained by a logarithmic spiral. However this work is related but relies on patterns I derived by geometry, algebra, and intuition. I just need to know if there is something significant here. I think the last equations I posted show a significance. It doesn’t mean an answer is concrete, but it may be a different yet simple approach to the problem. N = p * j or PNP = x * y I have more work, but I want you to look at this before there is even more confusion. I know it is a one way function. But the numbers are close. If I had assistance programming this thing maybe we would have an answer. I know that there is much confusion here. I am building this in real time. Just concentrate on the correctness of the last equation. I will answer any question to the best of my ability. Here is some videos. You will probably laugh at me, but it might answer any questions. There are inaccuracies due to my presentation ability and a few blunders in the equations. I have over 6 equations where y is in terms of x. I will share more, but I am not a professional so I am expected to be called naive. But don't let my ignorance stand in the fact that the last equations I posted to SFN may be something. I don't mind the feedback. I seriously believe in my equations.