Trurl

Well it worked here: Clear[x,pnp];pnp=2564855351; eqn=((pnp-(Sqrt[(x^2*pnp^4+2*pnp*x^5)+x^8])/pnp^4-(1-(x^2/(2*pnp)))*(pnp^2/x^2))); Solve[eqn==0&&x>=0,x,Reals]//N (*{{x41350.98025},{x6.387801493*10^11}}*) In[1]:= 41350 is close to 41227 By trivial you mean the division. I did not divide yet. I only used the equations. The magnitude should be close. I still have programming limitations on my own part. But I thought the number seemed reasonable. Close enough for good old brute force. What numbers do you get?

This is the smaller factor of: RSA-2048 = 2519590847565789349402718324004839857142928212620403202777713783604366202070 7595556264018525880784406918290641249515082189298559149176184502808489120072 8449926873928072877767359714183472702618963750149718246911650776133798590957 0009733045974880842840179742910064245869181719511874612151517265463228221686 9987549182422433637259085141865462043576798423387184774447920739934236584823 8242811981638150106748104516603773060562016196762561338441436038339044149526 3443219011465754445417842402092461651572335077870774981712577246796292638635 6373289912154831438167899885040445364023527381951378636564391212010397122822 120720357 Verify

I don’t see the point in Russia trying to influence elections. They’d probably want to but so does either side democrat or republican. The idea of collecting data is to know your target audience. Everyone wants an influential voice so the data is valuable. It would take some resources to power such a weapon. And the corrupt message could be drowned out in a sea of messages. No matter what your opinion someone disagrees. I often wonder if the Trump Biden thing is just to piss everybody off. Instead of having announcements that say go vote, they piss off everyone and it is a record turnout. So the morale is that if you don’t know the motivation behind the influence or control you can’t defend against it. Some things like money earned by selling data is common sense, but imho it would take some “power” to manipulate data on that scale. It would be like a president trying to control the entire government let alone the world. I was brainstorming ideas one night and thought what if we had a computer program that spread misinformation. Say it took your online profile and put in different addresses, phone numbers, and metadata. There probably is already software that does this, but I didn’t want to add to garbage already found on the internet, just the online footprint. I understand why China would want to influence us. And I think go ahead, we might learn something. I don’t know crap about China except they are communist and they take American jobs. Is this true. We know better than that. When I was in high school they said Japanese students are better in math and buy American. Our students are just as bright. Besides Japan are our allies. So I guess blaming China or math scores on Japan makes us study harder. But there are misconceptions all over the world. I guess it makes you loyal to your country and respect your leaders. Misdirection.

eqn=((pnp-(Sqrt[(x^2*pnp^4+2*pnp*x^5)+x^8])/pnp^4-(1-(x^2/(2*pnp)))*(pnp^2/x^2))); SetPrecision[NSolve[eqn==0&&x>=0,x, Reals]//N,94] Out[23]= 2519590847565789349402718324004839857142928212620403202777713783604366202070 Out[24]= 7595556264018525880784406918290641249515082189298559149176184502808489120072 Out[25]= 8449926873928072877767359714183472702618963750149718246911650776133798590957 Out[26]= 9733045974880842840179742910064245869181719511874612151517265463228221686 Out[27]= 9987549182422433637259085141865462043576798423387184774447920739934236584823 Out[28]= 8242811981638150106748104516603773060562016196762561338441436038339044149526 Out[29]= 3443219011465754445417842402092461651572335077870774981712577246796292638635 Out[30]= 6373289912154831438167899885040445364023527381951378636564391212010397122822 Out[31]= 120720357 Out[33]= {{x->4.098447549634527496690402228228115660800000000000000000000000000000000000000000000000000000000*10^37},{x->1.975537793137120663017279930682231182622035891422434710723887074852770653001767985540861473587*10^9 Why would a quantum computer render RSA useless?

If these numbers hold close, RSA is no more. I realize I have to expand the accuracy to 37 digits, but I got these numbers in 2 seconds. If they hold true so does the Pappy Craylar Conjecture! In[1]:= Clear[x,pnp];pnp=pnp = 2519590847565789349402718324004839857142928212620403202777713783604366202070 7595556264018525880784406918290641249515082189298559149176184502808489120072 8449926873928072877767359714183472702618963750149718246911650776133798590957 0009733045974880842840179742910064245869181719511874612151517265463228221686 9987549182422433637259085141865462043576798423387184774447920739934236584823 8242811981638150106748104516603773060562016196762561338441436038339044149526 3443219011465754445417842402092461651572335077870774981712577246796292638635 6373289912154831438167899885040445364023527381951378636564391212010397122822 120720357 eqn=((pnp-(Sqrt[(x^2*pnp^4+2*pnp*x^5)+x^8])/pnp^4-(1-(x^2/(2*pnp)))*(pnp^2/x^2))); NSolve[eqn==0&&x>=0,x,Reals]//N (*{{x41350.98025},{x6.387801493*10^11}}*) Out[1]= 2519590847565789349402718324004839857142928212620403202777713783604366202070 Out[2]= 7595556264018525880784406918290641249515082189298559149176184502808489120072 Out[3]= 8449926873928072877767359714183472702618963750149718246911650776133798590957 Out[4]= 9733045974880842840179742910064245869181719511874612151517265463228221686 Out[5]= 9987549182422433637259085141865462043576798423387184774447920739934236584823 Out[6]= 8242811981638150106748104516603773060562016196762561338441436038339044149526 Out[7]= 3443219011465754445417842402092461651572335077870774981712577246796292638635 Out[8]= 6373289912154831438167899885040445364023527381951378636564391212010397122822 Out[9]= 120720357 Out[11]= {{x->4.09845*10^37},{x->1.97554*10^94}} 4.09845*10^37 Hopefully is close.

I may have factored a RSA number previously unfactored. That is is the number crunching is right. Clear[x,pnp];pnp=pnp = 2211282552952966643528108525502623092761208950247001539441374831912882294140 2001986512729726569746599085900330031400051170742204560859276357953757185954 2988389587092292384910067030341246205457845664136645406842143612930176940208 46391065875914794251435144458199; eqn=((pnp-(Sqrt[(x^2*pnp^4+2*pnp*x^5)+x^8])/pnp^4-(1-(x^2/(2*pnp)))*(pnp^2/x^2))); NSolve[eqn==0&&x>=0,x,Reals]//N (*{{x41350.98025},{x6.387801493*10^11}}*) 2211282552952966643528108525502623092761208950247001539441374831912882294140 2001986512729726569746599085900330031400051170742204560859276357953757185954 2988389587092292384910067030341246205457845664136645406842143612930176940208 {{x->3.83952*10^37},{x->1.67814*10^94}} {{x->3.83952*10^37},{x->1.67814*10^94}} x should be just larger than 3.84*10^37 Test it. I hope it is close. Too bad there is no longer a reward for factoring RSA numbers 🤑

@Ghideon you are right much processing power is needed. I thought if I could get the size needed to test down to the size of a smaller RSA number that has already been factored, I could crunch it. Three hours no results. I had some help with the programming. A tester pointed out that I get 41351 instead of 41227. That is 124 digits off. But I am hoping is close enough to guess. Does anyone here do number crunching? I could use some tips on brute force crunching. Clear[x, pnp]; pnp = 2211282552952966643528108525502623092761208950247001539441374831912882294140 2001986512729726569746599085900330031400051170742204560859276357953757185954 2988389587092292384910067030341246205457845664136645406842143612930176940208 46391065875914794251435144458199; x = 30000000000000000000000000000000000001; While[x <=pnp,If[Divisible[pnp,x], Print[x]]; x+2]; While[x<=pnp,If[Divisible[pnp,x],Print[x]];x+2]; Clear[x,pnp];pnp=2564855351; eqn=((pnp-(Sqrt[(x^2*pnp^4+2*pnp*x^5)+x^8])/pnp^4-(1-(x^2/(2*pnp)))*(pnp^2/x^2))); Solve[eqn==0&&x>=0,x,Reals]//N (*{{x41350.98025},{x6.387801493*10^11}}*) In[1]:= While[x<=pnp,If[Divisible[pnp,x],Print[x]];x+2]; Clear[x,pnp];pnp=pnp = 2211282552952966643528108525502623092761208950247001539441374831912882294140 2001986512729726569746599085900330031400051170742204560859276357953757185954 2988389587092292384910067030341246205457845664136645406842143612930176940208 46391065875914794251435144458199; eqn=((pnp-(Sqrt[(x^2*pnp^4+2*pnp*x^5)+x^8])/pnp^4-(1-(x^2/(2*pnp)))*(pnp^2/x^2))); Solve[eqn==0&&x>=0,x,Reals]//N (*{{x41350.98025},{x6.387801493*10^11}}*) Out[2]= 2211282552952966643528108525502623092761208950247001539441374831912882294140 Out[3]= 2001986512729726569746599085900330031400051170742204560859276357953757185954 Out[4]= 2988389587092292384910067030341246205457845664136645406842143612930176940208 Computational processing required.

We are going to try and factor a RSA number that has yet been factored. No guarantees it will work. My estimate by graphing is that if we start at 4.0 X 10^37 and increase in value using brute force to divide into PNP, we may be rewarded with an answer. I understand it is still many values but at least we have a starting point. I also understand that if we are unsuccessful, we may be aided by finding the error of the factoring equation. Also graphs can be deceiving. If it is wrong starting point, it could be the graph is right, but the view of the graph is wrong. Clear[x,z, pnp]; pnp = 2211282552952966643528108525502623092761208950247001539441374831912882294140 2001986512729726569746599085900330031400051170742204560859276357953757185954 2988389587092292384910067030341246205457845664136645406842143612930176940208 46391065875914794251435144458199 z=pnp/(pnp/2) Show[ Plot[(( (((pnp^2/x) + x^2)) / x) /pnp), {x,5000000000000000000000000000000000000, 200000000000000000000000000000000000000}] ] 2211282552952966643528108525502623092761208950247001539441374831912882294140 2001986512729726569746599085900330031400051170742204560859276357953757185954 2988389587092292384910067030341246205457845664136645406842143612930176940208 46391065875914794251435144458199 2 Clear[x]; Plot[((pnp - (Sqrt[(x^2 * pnp^4 + 2 *pnp*x^5) + x^8])/pnp^4 - (1 - (x^2/(2*pnp))) *(pnp^2/x^2))), {x,5000000000000000000000000000000000000, 200000000000000000000000000000000000000}] Clear[x]; Plot[(1/((pnp / (((pnp^2/x) + x^2)) / x))), {x,5000000000000000000000000000000000000, 200000000000000000000000000000000000000}]

105951 105950 105909 105910 105911 Ok on an odometer when there are at least 3 matching numbers say 555 or two sets of repeating numbers, say 5500, then we will try to predict when each occur chronologically on the odometer. Sure you could just fill in the numbers with the corresponding numbers. But imagine these numbers were related to Prime distribution. The pattern is harder to see with the odometer as it moves linearly. Imagine you have a regular odometer. It goes zero through nine. So in the single-digit place of the odometer (the start of counting), you note that 3, 5, 7 are Prime. So now you go to the tens-digit. And note that 3+1 or 3+3 or 3+5 or 3+7 are eliminated as Prime. To get another Prime number you would have to add an even number to 3, 5, or 7. Of course adding an even number doesn’t always result in a Prime. This is just a graphical representation of a sieve. But just as repeating numbers in the odometer are hard to predict linearly throughout the revolutions of the odometer, are we not doing the same thing when looking for patterns in Prime numbers? I study Prime numbers because I like finding patterns. Patterns can confuse or look like they could be there, but patterns are what we see in math. I might have stretched the truth when I claimed RSA was in trouble, but that one-way function is why I started all this math in the first place. The odometer sieve would require a lot of calculation. Again it would only show what is going on. It is the same with my graphs. I can only estimate where the semi-Prime factor is on a graph. Graphing 128-bit numbers and analyzing the graph is a challenge, but necessary to prove as the curve on the graph approaches zero x approaches the smaller Prime factor. That is where I believe if the graph holds true, for larger N’s, it will be superior to brute force. But as the graph becomes larger and more difficult to evaluate so does choosing an N. I have read that if N becomes too large, the enciphering of the message becomes too cumbersome. In a future post I will be sending a graph. But It is important for anyone reading this to share if they had any results with the graph. I have tried to make the graph more useful (less test values) by inverting the equation.

Clear[x, pnp] pnp = 2564855351 Show[ Plot[(( (((pnp^2/x) + x^2)) / x) /pnp), {x, 0, 60000}] Graph this equation. It is the inverse. It should make it easier to find the SemiPrime. It will decrease number of trails, but on small numbers will still be more time than brute force. It will however give you a graphical understanding of the smaller SemiPrime. Remember 2 unknowns should be impossible.

I also wanted to say I’m happy to hear this post encouraged you to research SemiPrimes. That is what it is all about. I was going to be an adult educator until the professor failed me. But that is another story. I also hope that if you take the inverse of the dozens of equations that it will make the graph better for visual inspection. I also would be interested in what you are working on. Maybe you will share in the forums someday. BTW does anyone know what the picture of the writing on the wall is?

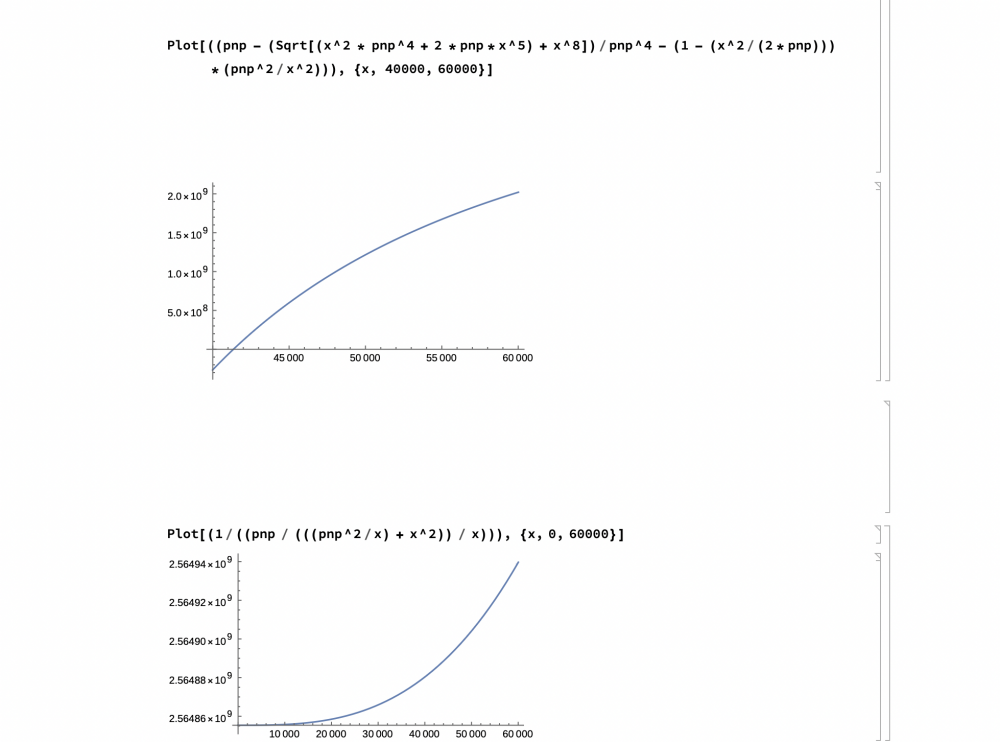
You are right about the brute force. I don’t know how useful it is when the smaller factor is occurring close to zero anyway. But what is given me a glimmer of hope is the first graph of my last post cross the x axis at around 41227. That’s where it appears to cross but computer generated graphics can be deceiving. If anyone could show where y on the graph equal zero that is the x intercept of that fist graph of the last post, it would be well appreciated.

Ok, I haven’t been here in 3 months. I was walking around and read the writing on the wall. And it made me think I should be working on mechanics instead of such abstract ideas of factoring SemiPrimes. But my work was not without reward. But of course graphs can appear deceiving. Often graphs show a limited view. (Like in the old days of CAD when you couldn’t revolve the view in 360 degrees. You had to change the angle of the view by typing in coordinates). The question is, “Is this graph deceiving?” Clear[x, pnp] pnp = 2564855351 Show[ Plot[(( (((pnp^2/x) + x^2)) / x) /pnp), {x, 0, 60000}] ] Plot[((pnp - (Sqrt[(x^2 * pnp^4 + 2 *pnp*x^5) + x^8])/ pnp^4 - (1 - (x^2/(2*pnp))) *(pnp^2/x^2))), {x, 40000, 60000}] Plot[(1/((pnp / (((pnp^2/x) + x^2)) / x))), {x, 0, 60000}]

This code works!!!!!!! Working Mathematica Code: Clear[x,p]; p=2564855351; x=3; Monitor[While[x<p, If[(x*(Sqrt[p^3/(p*x^2+x)])-p)<0.5, Print[x]; Break[];]; x+=2;]; If [x <= p, While[x<p, If[Divisible[p,x], Print[x]; Break[];]; x +=2;];], x] 3 41227

p = 2564855351; x = 3; Monitor[While[x <= p, If[(x*(Sqrt[p^3/(p*x^2 + x)]) - p) < 0.5, Print[x]; Break[];]; x += 2; Missing parentheses, but the logic is there. The language is Mathematica. I collaborated with another Mathematica coder. I’m not familiar with the “Monitor” class. But this class is the representation of everything I have posted. If it is the syntax I will have to consult more Mathematica coders. Attention all coders!!!

p = 2564855351; x = 3; Monitor[While[x <= p, If[(Sqrt[p^3/(p*x^2 + x)] - p) < 0.5, Print[x]; Break[];]; x += 2;]; If[x <= p, While[x <= p, If[Divisible[p, x], Print[x]; Break[];]; x += 2;];], x] First function corrected: p = 2564855351; x = 3; Monitor[While[x <= p, If[x*(Sqrt[p^3/(p*x^2 + x)]) - p) < 0.5, Print[x]; Break[];]; x += 2; Same as all my recent descriptions.

Well leaving out the x was a happy accident. It just shows again x times y = p and we are just using algebra. That is why the second part of the program used division. The first algorithm found where x value of the small factor approached zero value at y. I put the value of y at p minus x times y so it is easier to find. I could have said x at factor and y equals pnp. I said within range because there is some error with x. It is close but within error. The equation is too complex to solve for x even though it has x as the only unknown. I say approaches because I am plugging in a test value of x to find y. That is why I graphed it. I know it is not pretty math and is more of a hack. But using test values you know the area of the factors because the further away the y value on the graph is from zero the further away you are from the factor.

p = 2564855351; x = 3; Monitor[While[x <= p, If[(Sqrt[p^3/(p*x^2 + x)] - p) < 0.5, Print[x]; Break[];]; x += 2;]; Syntax error. Should read: p = 2564855351; x = 3; Monitor[While[x <= p, If[x*(Sqrt[p^3/(p*x^2 + x)]) - p) < 0.5, Print[x]; Break[];]; x += 2;]; That is why it wasn’t working. It was y, the second Prime factor. But we would have no way of knowing when y was reached. Multiple y by x to get p. Subtract p and the y of graph equal to zero. That y intercept is where x approaches the value of the smaller Prime factor.

The problem is it is Sqrt[(x^3*pnp^3)/(x^3*pnp+x)-pnp Where pnp is the constant SemiPrime. 2564855351 in this case x is the value on the axis. Where y on the graph equals zero, x approaches the smaller SemiPrime. I believe in your graphs y is variable. I am working on testing the program. But if you take p = 2564855351; x = 3; Monitor[While[x <= p, If[(Sqrt[p^3/(p*x^2 + x)] - p) < 0.5, Print[x]; Break[];]; x += 2;]; and display x when it breaks it should be within range of the smaller Prime factor. I know testing sounds simple enough but my computers and software are aging. Software upgrades faster than I do. All my software is scattered across 5 computers. And I don’t think Win7 and XP systems are safe on the internet. But that is just my computer maintenance problems. Hope this helps.

There are no anomalies. When you graph the equation, the x of the graph (you just graphed) equals the smaller Prime factor where y of the graph is or around zero. There are no tricks. That is why I called it Simple Yet Interesting. The code I posted was generated by ChatGPT. It simplified the equation. You should try it in Mathematica. It is not meant to be efficient but the first function should break (and print) near zero and estimate the smaller factor x. I have already posted on this. Let pnp = 2564855351 When x = 41227, the (x*y) part of equation equals 2564855365.5 https://www.scienceforums.net/topic/124453-simple-yet-interesting/page/7/#elControls_1258420_menu Hope this explains what I was attempting to do. I need to post another, larger example. If the program from ChatGPT works you should be able to modify the testing steps ( from every odd number to x+=22 or larger) The one thing that needs checking is how GPT simplified the equation. That is why I said test for lager Primes. Because 2 known Primes multiplied together will equal zero in the equation if they form a SemiPrime.

@Ghideon And anyone interested Yes. I am still dividing and finding a square root in my calculations. How could it be faster than the original recursive division? Probably not faster, since when you start at 3 the unknown x is closer to zero than pnp anyway. But the advantage is you don’t need to test those values in my equation that don’t occur next to zero. This zero is unique to pnp. It also occurs in sequential order. So, if you subtract the left side of the equation by pnp and it is, say 5, you know that x is smaller than the tested x at that value. I know it has many faults, but it does provide a unique graph that may contain some useful analysis. I think it will prove more useful as pnp increases in value. But it is difficult for me to test. I will try to factor the largest semi-Prime posted earlier. But that is why I posted here in the first place for help testing. I realize my algorithm isn’t faster than plain division, but that isn’t what it was intended to do. I need outside eyes because I created the algorithm and am biased, but finding semi-Primes is not the only part. Instead, it is to exploit a pattern in factorization.

3x+1 if odd x/2 if even So why not create a sieve of multiples of 2, 4, and 8? When x equals a logarithm of 2, 4, or 8 then x/2 repeated equals 2. 2*2*2*2… 4*4*4*4… 8*8*8*8… These 3 logarithms of 2, 4, and 8 encompass all the numbers that reduce to 2 when repeatedly divided by 2. What am I missing? Did I break the rules of the pattern? I am trying real hard not to factor semiPrimes. I did not research the problem yet. I am only working with 3x+1. I realize that this is more complex with larger numbers. I am just stating a simple example.

@Sensei @Ghideon I had help on this program. A good Samaritan put the code into ChatGPT and it supped-up the code. I still don’t know if it will run faster with larger Primes compared to standard recursive division. I think it gives a picture of what is going on with the factoring. x will only occur around zero on the graph. Again, I don’t know how to measure any efficiency of the program. Obviously with small Prime products (pnp), it will not show any improvement with factoring the semiprime. Again, I am breaking a resolution not to enhance RSA. But I wanted to share some final thoughts on this project I have spent great effort on. I think my next project will be Microsoft Kinect or 3D Printing. A friend bought me a book on Nichola Tesla for Christmas. It has his messages. However, the messages are encoded in puzzles and cryptograms. I thought I could write a simple Mathematica program and decode them. If the program works, I will share every detail. Here we go again. LoL. At least it’s not RSA. Even video games would be a good break from RSA. I know what you are thinking why would I give such information away. That is if you really believe in my program. I know such information is valuable, but if no one attempts to find large Primes with it I don’t know if the program even works. That is why I shared everything in the message board. I have shown my case. Please prove it right by finding large Primes. p = 2564855351; x = 3; Monitor[While[x <= p, If[(Sqrt[p^3/(p*x^2 + x)] - p) < 0.5, Print[x]; Break[];]; x += 2;]; If[x <= p, While[x <= p, If[Divisible[p, x], Print[x]; Break[];]; x += 2;];], x]

One of my resolutions this year is to stop trying to enhance RSA cryptography. I have been at it as early as 2006. In my first attempts, I stated that a logarithmic spiral could define a pattern in Prime numbers. I still believe this. And it is inherently feasible because logarithms already explain many patterns. But my ideas are the same in all my posts: x * y = pnp. If I had just left the equation at: x * (pnp / x) = pnp ; it wouldn’t have been helpful. I had to find a way to put y terms of x and pnp that was useful and equaled more than 1 =1. The enhanced equation still may be difficult to solve, but with only x as the unknown I could substitute x along the graph and when that value minus pnp approximately equaled zero, the value of x that caused that zero is the smaller Prime factor. Well despite the fact if you believe me or not Or if this is even useful (I believe it is useful), you could set up an equation similar to this isolating x and testing it along a graph for any pattern. It may be a challenge to put y in terms of x and pnp that only solves the desired pattern, but it would be a shot to analyze the series in ways not done before. So, as I break or fulfill my resolution, I ask even though it would still be challenging to break RSA with this method, is the method itself useful in trying to find patterns where this is no pattern? x* y = pnp x * (Sqrt[ (pnp^3/(pnp * x^2 + x) + (x^4/(pnp^2 + x) )] ) = pnp x * (Sqrt[ (pnp^3/(pnp * x^2 + x) + (x^4/(pnp^2 + x) )] ) – pnp = 0 Let pnp = 2564855351 When x = 41227, the (x*y) part of equation equals 2564855365.5 Not bad for government work.