Jump to content

Trurl

Senior Members
 View Profile  See their activity

  • Posts

    568

  • Joined

  • Last visited

  • Days Won

    1

 Content Type 

Everything posted by Trurl

  1. Trurl
    But isn’t a golden spiral a type of log spiral? What if the stair steps of the Riemann graph could be put geometrically on to a logarithmic spiral? And with various logarithmic spirals able to be drawn changing the “amount of step?” But I understand you point. I have seen some good demonstrations of the golden spiral on YouTube.
  2. Trurl
    I have to look at it again. I think the problem is the author claims a significant pattern without an explanation. So what he said could be right but we don’t know the context. I have issues with this journal entry. It tells us a history we don’t need to know and has one paragraph of content. But I could not find any other articles relating Primes to biology.
  3. Trurl
    I am interested in how Prime numbers relate to biology. A double helix is made of 2 logarithmic spirals. And there is a field of bioinformatics which I know nothing about. But are there relationships with Primes in biology and if so where should I begin. That is with no training in biology. I found a journal article on the subject but it didn’t get interesting till the last paragraph. And the article didn’t explain these relationships. https://d197for5662m48.cloudfront.net/documents/publicationstatus/39104/preprint_pdf/e048de98234bc62175f7f7c0a366e35b.pdf I found it interesting that Prime quantities are found in the nucleotides. But I don’t think it is enough to establish a pattern. I believe that you can express the stair steps of the Riemann Hypothesis can be graphed in a logarithmic spiral. Can you apply the graph of a logarithmic spiral to a double helix.
  4. Trurl
    Baron, did you use A.I. to write Prime Mechanics? To me it is an attempt to explain the World nonsensically. Like a pun. Like something Stanislaw Lem would write. It would make a good sci-fi story. Or an excellent alternative world for fantasy or video game. I don’t say that to make fun of your work. I don’t know higher physics. And it could be higher physics sounds like a fantasy world anyway. I am interested in the Prime number aspect. How are you relating Primes to physics? Do Primes exist naturally or did man create them? To me your theories are just a thought experiment. There is nothing wrong with being wrong. You ideas are uncanny, but that is good when it comes to Primes.
  5. Trurl
    I know we have physics and still can’t travel the speed of light. But aren’t engineers focused on mathematics in training? I know math is a lot of thinking and building is more tangible. But how do you build incorporating mathematical principles and not discover them. Today we take the math as something your taught. But when written word isn’t developed how do you share the law of sines? Math is a language. But it can also tell time. Could it be a civilization that was mathematically advanced was technologically advanced? And what type of math a civilization has produced will determine the future of that society’s technology? I think that is why everyone in the forum likes math. And we talk about it in spare time. We are looking to build the society through math.
  6. Trurl
    I saw a debate once. I thought it was here on SFN. Was math created or discovered? Is math created to explain the world or did it always exist and we happened to notice it? Math is a language understood by everyone. I wonder how such advanced buildings were constructed before history was recorded. I don’t think anyone can explain were it came from. My question is how can you be mathematically advanced and not be technologically advanced?
  7. Trurl
    So in 2007 I tried to make a logarithmic spiral show a pattern of Prime numbers. Long story short, I couldn’t get it to work. It was before I heard of the Riemann Hypothesis. The area of the logarithmic spiral could be set to the integral of li(X). I am not claiming it works. I am asking what you think of placing the Riemann Stair Steps to a logarithmic spiral. I never had my own math this old before. I can’t remember what I was thinking when I wrote it.
  8. Trurl
    That’s the book. The authors wrote it working in just 1 week a year for 10 years. The one I ordered wasn’t too expensive. I think the book is printed as you order. Excellent read. It puts the number theory into sentences. It is good for undergraduate or lower level graduate. That is my level. For me the notation of number theory is above my education. I know the math of things like the Riemann Hypothesis is complex, but the idea should still be generalized in words. Didn’t someone say if you can’t explain the problem simply, you don’t understand it.
  9. Trurl
    You are right I need to work at becoming a better programmer. I don’t know much programming beyond what I learned in college. I tried to bridge the gap by using math scripting in Mathematica. It gave me access to things that require some more know how than my current level. And I am not against asking Chat gpt to program it for me. But remember, programming can find a counter example, but cannot prove math. I also am still looking for a better way to analyze graphs. I want the computer to analyze the graph according to math algorithms I input. NTuff linked to a college presentation which referenced the book: Prime Numbers and the Riemann Hypothesis. I have been reading this book. The book makes the topics understandable, but the content is still complex. The is no easy way to put the Riemann Hypothesis, but this book explains the problem and does a good job at explaining the approaches to a solution. Reading in this book, I have wondered if I have stair steps in my graphs. And if I should be concentrating on finding large Primes instead of finding a pattern. I was looking at my odometer again today. It hit 097777 and then 097797. That is a short time to have 97 and 77 repeated. And it made me wonder is the reason we can’t find a pattern in Primes is because we are counting? 2, 3, 5 ,7 …. Is there a way to find Prime numbers in we don’t go by counting numbers? I know this is advanced and I don’t have a solution, but can you see what I mean? Does that statement make sense?
  10. Trurl
    Ok. So the views under the posts aren’t exact. But I was wondering if they could still be useful. On my Posts: Simple Yet Interesting and Prime Products One More Time, I have over 40,000 combined views. So these post are seen a lot, although 40,000 is much larger than the precise number of views. Why am I concerned with the number of views? Well I thought it was a pattern in factorization of semiPrimes. Obviously if it would have worked, RSA would no longer be in use and most digital signatures wouldn’t be able to authenticate. But we would have a pattern of Prime numbers in return. But I look on the bright side. Maybe there is still use of the work. Maybe it can find larger Prime numbers. My goal started as trying to find a weakness in RSA and then a pattern in factorization. It sounds disastrous to try and attempt such things, but remember people and governments are attacking ciphers all the time. Wouldn’t it be better to know RSA is flawed. That is, if it is. And since we don’t have to worry about the destruction of RSA, my challenge to the viewers is to find a legitimate application for Simple Yet Interesting. That is, the Pappy Craylar Conjecture. I am researching sources on Prime numbers, in order to see what is already known and try and find an application for the Pappy Craylar Conjecture. I know views aren’t the goal of science. But the reason I wanted views was that someone would come and prove my work. There is a networked science in the book Reinventing Discovery by Michael Nielsen, These posts were my attempts at networked science.
  11. Trurl
    I’m going to ruin the Matrix Trilogy like Amy ruined Indy Jones for Sheldon on the Big Bang Theory. She ask why Indy stopped the Germans will they opened up the Arc and died anyway. So why did the machines in the Matrix use humans for batteries when they have the ability to reach the atmosphere and space. In the first movie Morpheus says we scorched the sky. ( A attempt to eliminate solar power?) But in the 3rd movie Neo and Trinity fly above the scorched sky. So if machines don’t need us for batteries, why not destroy humans and we go to all the trouble of a simulated world? I think the machines didn’t want to destroy their creators, the humans. Maybe the simulated world is to prevent wars between machines and humans? Maybe it means the human mind is superior to the machines? Maybe the machines are wondering if they have a soul? Maybe the machines know the human body is a machine and there should be similarities between machines and humans? But why do machines fight for the Earth when they can inhabit all of space? And who governs the machines? Do the machines have free will?
  12. Trurl
    You’re right that my programming skills are lacking. But as with large Primes programming, large numbers in C++ are difficult. In the Simple Yet Interesting, I graphed 2564855351 and it resulted in zero. That is not the same as the Riemann zeroes, but I want an educated guess to plug and chug. One mathematician said trillions of zeroes have been found at 1/2. But again I don’t know how to program imaginary numbers. I rely on Wolfram Alpha. But I also want to program something different; something of mine. Should I stick with Mathematica? Also I need something to plug and chug. But I guess finding what to plug and chug is up to me. But what is a good starting point? I treat working with Primes as a learning exercise. They are fifty math problems in one. But the solution may not even be possible. The computer can’t make a proof. But it can disprove if it isn’t at 1/2.
  13. Trurl
    The podcast is too vague. There are just too many people with papers on the Internet that claim to have solved the Riemann Hypothesis. But if you are just searching for zeroes, are there any equations that you could just plug and chug numbers into? I have seen s^-1 summed. But I am searching for other ways to test for zeroes.
  14. Trurl
    Link to 2013 paper: https://annals.math.princeton.edu/wp-content/uploads/annals-v179-n3-p07-s.pdf
  15. Trurl
    Thanks NTuff. That presentation is excellent. It started off simple and you see how complex it gets. It defines the problem in a short series of slides. And that is what is important: understanding the problem. Wikipedia’s description is hard to understand. I asked Chat gpt if an equation that equals zero at the Prime numbers could relate to the Zeta function. It said no because the Zeta function determines distribution. It said the Mangoldt function would relate better. This may or may not be true, because the presentation showed how the Mangoldt function relates to the Zeta function. So how does the equation I put in “Simple Yet Interesting” compare to Mangoldt? BTW the equation for the odometer is not the one I am comparing to the Zeta function. It is just a model I used to picture patterns as I drive. But I think the problem of finding the distribution of repeating numbers in the odometer relates to the problem of the distribution of Primes. The picture of the podcast is where I heard that an Indian mathematician uploaded his proof of the Riemann hypothesis and no one can tell if he is right.
  16. Trurl
    Awesome now we have a formula. But what is we counted all different digits for 3 combinations and wanted to find how many occur between any given number. Say every 1001 units. I know they will all occur between 000000 and 999999 but what if you say 064064 and 065065 are 1001 distance apart. But 6400640 is significantly larger. If you chose a range are there more combinations occurring linearly from say 000000 to 030000 than 050000 to 080000? The combinations all occur over the range of real numbers, but do they occur evenly over an equal distance from zero? In other words, “is this pattern evenly distributed over the linear odometer? That is as they occur “counting.” (The odometer is just counting.) I have been working with this for quite some time. When my odometer turned 096096, I thought it was a reason to share and see if this meant something. 019019 091091 901901 092092 029029 209209
  17. Trurl
    Consider these problems: An odometer turns so that the first numbers equal the last. For example, 096096 has 3 numbers that equal. But can you tell for which numbers this works for. For instance, if you had 123123 it would have 3 equal numbers, but it would take longer to get that size number. If 012012 occurred how close would it be to 021021. Would smaller numbers be closer of further away from similar patterns of the same series of numbers. Obviously, you could argue that because we are going through all real numbers the occurrence of numbers and patterns are equal. The pattern is simple. But going linearly (counting) makes this observation difficult to see. And that is how I feel with patterns in Prime numbers. Most attempts at finding a pattern are linearly starting at 1 and counting. But I hypothesis that is why no pattern is found. Problem 2: We all leant that a modulus can be described by a clock. But what if you had 2 or more clocks that were rotating at different times at different rates of speed of rotation. Would they every have the exact time? That is rotating to infinity. And if they never do have the same time, could you prove it mathematically? These are just some questions I had. I found a book on the Riemann Hypothesis that is geared to the undergraduate. But it is better is it easy to read so that I can better understand it. I heard in a podcast that an Indian mathematician claimed to have proved Riemann’s work. He posted it on the Internet. It has been years, and no one can make any sense of it. That is why it is best to keep it simple. You could spend years studying the Riemann Hypothesis and never know what Riemann knew. There is also a rumor that after Riemann passed away his maid took most of his papers on his desk and burnt them. She never explained why she did that. So, a pattern of Primes could have been solved. Instead, we are looking at what was published. I’m just looking for simple ways to understand it.
  18. Trurl
    Sounds dangerous to use race and ethnic labels. But what if in studying the genome there are more “classifications?” These classifications may be rooted in science but would also be misused.
  19. Trurl

    Ask Chat gpt about the Pappy Craylar Conjecture.

  20. Trurl

    Pappy Craylar Challenge: Compare Zeroes of Zeta Function

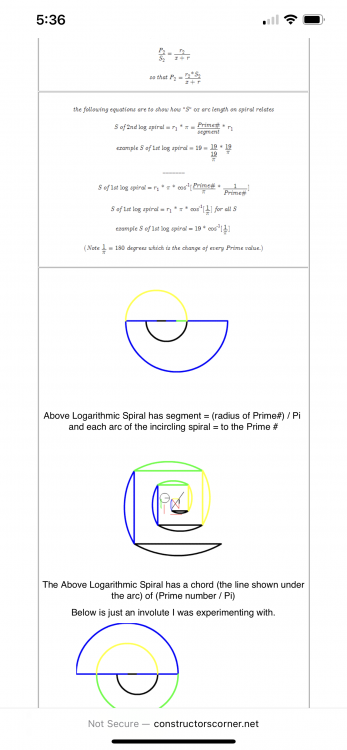
    I have been doing some research into the Riemann Zeta Function. The truth is I really don’t understand it. I get the main idea that zeroes describe Prime numbers. And only ½ holds all the zeroes. But as a layman looking at that, I just think to myself that is because 2 is the only even Prime number. That is if you consider it Prime.

    I took a different approach in the Simple Yet Interesting thread. I look for patterns in factoring, specifically in the products of 2 Prime numbers. I reviewed other methods, and they seem to be concentrating on a series. My attempt is simple in that I find equations where pnp can be explained by itself and one of the Prime factors. I knew it sounds absurd. How can you find the unknowns. But I put pnp = pnp and solve for x. Compared to the Zeta function my attempt is primitive. My equation also has the problem of not being able to solve the polynomial equation. Instead, I graph it, plugging in x to see which values are true that complete the equation.

    There is also a question of zeroes. I too have zeroes. Except the zeroes on the graph occur at the semiprimes. And the factors of that semiprime are now known as the Prime numbers x and y in the equation. Instead of a real and imaginary number part, there is just real numbers.

    That is my challenge to you. Can you relate my equation to a series. (I have put a series of semiprime numbers already in the thread.) But if you take the series and plug it into the Zeta Function, what do you get? (Yes, I don’t understand all the Zeta Function. But what if you took the series in the last post of Simple Yet Interesting and used that equation as f(x) equal to the Zeta Function. I have not worked this out yet, but x at f(x) in the equation can be set to equal a zero.)

    As always this is a challenge to write. If you have any questions post them.

    My challenge to you is to Find an equation that can put the Pappy Craylar Conjecture equation into a series that can be written or compared to the Zeta function.

  21. Trurl
    3rd Challenge: Graphical Representation: I have claimed that a logarithmic spiral could be drawn to show a pattern in Prime numbers. It is easy to claim but hard to draw. Here I challenge you to draw a logarithmic spiral that explains the last post’s graph of PNP and where it equals zero. But what is the previous post finding a semiprime where the graph equals zero, there was a modified sine wave that explained the graph? So, you have numbers at PNP at zero with x and y (the Prime factors), with the sine curve osculating above and below zero. And the sine curve at the same time is experiencing resonance. Growing larger in magnitude as the value of PNP increases. Could not a logarithmic spiral explain this? And couldn’t a differential equation explain this resonance like a differential equation explains resonance on a spring? And if you put the graph in 3D, does it make a helix? And could it be useful to define changes in helix such as those that describe DNA. Obviously, that is wishful thinking but new ideas bread new ideas.
  22. Trurl
    Well I’m glad you know the answer because I don’t. So much of today’s programming is using existing libraries. That is why I like reading cryptography protocols because the main idea is simple. I really am not a good programmer. That is why GPT is a game changer. I can’t learn all the interfaces. And things I have learned are outdated. Remember Flash. I think GPT might fix this problem of languages and formats. But do you think we will end up with lots of code we have no idea how it works?
  23. Trurl
    Sounds like a challenge to me. Someone in the forum probably has an answer. Not my area of expertise, but what if we had a couple members ask ChatGPT give us starting point?
  24. Trurl
    I posted a challenge in Simple Yet Interesting. I am serious. I want to see if someone here is a better programmer than me. It is a programming challenge as much as a math challenge. I think it is a good first challenge. Challenges are challenging to write. I don’t know if most of you remember that before the Internet, magazines were the way to distribute information. For example, the RSA problem appeared in 1979 Scientific American. Also, there was a feature called the Amateur Scientist for amateur experiments. Good magazines are hard to find today. But it leaves something that could be formatted to fit the web. If you know of any good programming challenges or ideas, reply to this post.
  25. Trurl
    Where x * y = pop When y = Sqrt[pnp^3/(pnp*x^2+x)] So that, x* Sqrt[pnp^3/(pnp*x^2+x)] = pnp pnp – pnp = 0 Let x equal any Prime number. 5 for instance. Graph x = 5 at x on the graph at that instance = pop So where 5* Sqrt[pnp^3/(pnp*5^2+5)] – pnp = 0, then pnp is a semiPrime and we can plug it into the equation and find y (the larger Prime number). And if we continue to graph over all real numbers we will find every Prime number in existence. This is my programming challenge to you. Remember the math does not have to work to complete the challenge. The challenge is to see how fast you can prove it wrong or correct.
×
×
  • Create New...

Important Information

We have placed cookies on your device to help make this website better. You can adjust your cookie settings, otherwise we'll assume you're okay to continue.