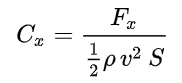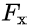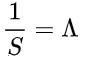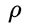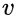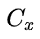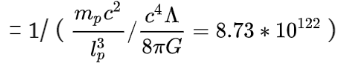stephaneww

Hello and Hum ... it is nice to calculate: ΩΛ,tH = 3 Λ c2 tH2 with tH= Planck time : 5.391247*10^(-44) s c = 299792458 m/s and Λ = 1.102 * 10^(-52) m-2 ΩΛ,tp= 9.60 * 10-123 we make: (1 / ΩΛ,tp)* 8 π / 3 = 8.73 * 10122 to have the value of the vacuum catastrophe: (with vacuum energy value in QFT = lp^(-2) = 3.83 *10^(69) m-2 8 π * 3.83 *10^(69) / 1.105 * 10^(-52) = 8,73 * 10^(122) basically the vacuum catastrophe would be the density parameter of dark energy at Planck time in the ΛCDM model and that would be no problem. Does it make sense or not ?

Hello I know that its fairly accurate value is 8.73 * 10122 when we are in the order of magnitude of 10120. But I also know that there is a value in the order of magnitude of 1060 I would like to know a value with a few decimal places and the exact exponent for the order of magnitude of 1060. Thanks for your answers

Hello for H0=67.66 km/s/Mpc i.e. tH = 4.5606*1017s, and ΩΛ = 0.68694 we have: ρc,tH = 3 / (8 π G tH2) = 8.5988 * 10-27 kg/m3. - by dimensional analysis, looking for the value of the cosmological constant Λ of dimension m-2 and with a mixture of relativity, deterministic Planck units we have: Λ = 8π ΩΛ ρc,tH lp / mp = 1.1026 * 10-52 m-2. [math]\Lambda = 8 \pi \Omega_{\Lambda} \rho_{c,t_H} \frac{l_p}{m_p}=1.1026 *10^{-52} m^{-2}[/math] - This is exactly the value of the cosmological constant of the ΛCDM model. The formula of the density of the" quantum vacuum" at our time tH0, seems to correspond to the formula of the density of the quantum vacuum at the time tp. This comes from a toy model, whose only values we can be sure of are tp and tH thanks to the ΛCDM model. Is this an acceptable solution to the cosmological constant problem . (???) we have the quantum field theory energy with this equality : 8π/3 ρc,tp lp / mp = 3.8281 * 1069 m-2 =lp-2 [math] \frac{ 8 \pi}{3} \Omega_{\Lambda} \rho_{c,t_p} \frac{l_p}{m_p}=3 8281.*10^{69} m^{-2}[/math] note that mp / lp is the Planck linear mass.

Hello. The weak point of my mathematical solution is that it does not allow for physical interpretation. Below I will try to propose an interpretation of the cosmological constant problem : The cosmological constant problem as a drag coefficient. ? Having read "the particles of a perfect gas have speeds close to those of light" and knowing that the formula of the cosmological constant can be interpreted as the expression is of a perfect fluid at negative pressure during my research on search engines I found the notion of drag coefficient . Its definition and its dimension seemed interesting enough to me to make a numerical verification with the data / formulas that I use or propose: Definition of the drag coefficient : adimensioned. With : = Planck force ( = c4/G ) because the cosmological constant has the dimension of the inverse of a area. density in Planck units. (mp/lp3, Kg/m3) take here the value of c, speed of light (speed of "agitation" assumed from the pressure of the cosmological constant), In the end we get this calculation of the vacuum catastrophe with Planck's values : I think within a factor of 16 pi. Note: we can formulate the cosmological constant problem indifferently with zero-point energy or Planck's units, the order of magnitude is the same. Is it a possible interpretation ?

Hi, See: https://constantecosmologique.fr/ available in English What is your opinion please?

how to explain then that rho_c * c^2 = [M L^-1 T^-2] has the dimension of a pressure? where is the error?

we can give it the dimension of a pressure by multiplying by c^2

Okay, if the radiation is missing from rho, it makes the cross-reference a lot harder to check.(if I understand what you are saying). For H=67.74 (input) I have rho_c=8.61916 10^-27 kg/m^3, against rho_c=8.62765 10^-27 kg/m^3 in the calculator I'm really uncomfortable with state equations.🙄

I confess I don't really understand. rho depends theoretically only on H? but we don't find it for H input nor for H ouput. I kept this value

Hum, I don't known if that calculator is ok for all datas : for example H input (=67.74) isn't H output, and there's a little discrepancy I don't understand about rho. [tex]{\scriptsize\begin{array}{|r|r|r|r|r|r|r|r|r|r|r|r|r|r|r|r|} \hline z&T (Gy)&H(t)&rho, kg/m^3&OmegaL&OmegaT \\ \hline 1.09e+3&3.70793e-4&1.55837e+6&4.61214e-18&1.28867e-9&1.00e+0\\ \hline 3.39e+2&2.48188e-3&2.47284e+5&1.16132e-19&5.11790e-8&1.00e+0\\ \hline 1.05e+2&1.52326e-2&4.16481e+4&3.29421e-21&1.80424e-6&1.00e+0\\ \hline 3.20e+1&8.97471e-2&7.17048e+3&9.76466e-23&6.08678e-5&1.00e+0\\ \hline 9.29e+0&5.20128e-1&1.24469e+3&2.94228e-24&2.02004e-3&1.00e+0\\ \hline 2.21e+0&2.96640e+0&2.23251e+2&9.46559e-26&6.27909e-2&1.00e+0\\ \hline 0.00e+0&1.37737e+1&6.74009e+1&8.62765e-27&6.88894e-1&1.00e+0\\ \hline -6.88e-1&3.29612e+1&5.63238e+1&6.02483e-27&9.86506e-1&1.00e+0\\ \hline -8.68e-1&4.78813e+1&5.59720e+1&5.94981e-27&9.98945e-1&1.00e+0\\ \hline -9.44e-1&6.28349e+1&5.59450e+1&5.94406e-27&9.99911e-1&1.00e+0\\ \hline -9.76e-1&7.77911e+1&5.59427e+1&5.94357e-27&9.99993e-1&1.00e+0\\ \hline -9.90e-1&9.27477e+1&5.59428e+1&5.94360e-27&9.99988e-1&1.00e+0\\ \hline \end{array}}[/tex] ... and there is this after PLANCK 2015 : https://en.wikipedia.org/wiki/Planck_(spacecraft)#2018_final_data_release

This is the case we find the formula of the critical density (*c^2 to have J/m^3) with a factor 3, so it works with the evolution of [math]H[/math] in time The method for finding [math]B'[/math] (Hubble constant) is the same as that used to determine the hypothetical [math]B[/math] (cosmological constant) value here: https://www.scienceforums.net/topic/122453-an-attempt-to-approach-a-notion-of-solubility-in-cosmology-to-explain-the-cosmological-constant/ In short, the method seems reproducible. My question therefore concerns the validity of this hypothesis. demonstration : [math]A=\frac{c^7}{G^2 \hbar}[/math] [math]B'=\frac{1}{(8 \pi)^2}(\frac{H^2}{c^2})^2\hbar c[/math] [math]A B'=\frac{c^8}{(8 \pi)^2 G^2}\frac{H^4}{c^4} [/math] [math]A B'=\frac{c^4 H^4 }{(8 \pi)^2 G^2} [/math] [math] 3 \sqrt{A }\sqrt{B'}=\frac{3 H^2 c^2}{8 \pi G} = \rho_c c^2 [/math] https://en.wikipedia.org/wiki/Friedmann_equations#Density_parameter (the c^2 factor for the critical density differs between the French and English versions of wikipedia, hence a small float on this point)

Okay, thanks. But that's not what I'm asking about. My question is: can this new application of dimensional analysis of my hypothetical value [math]B[/math] in QM of the cosmological constant be validly duplicated for [math]B'[/math] with the Hubble's constant ? In view of the result, I think yes. Otherwise for the actual measurement of the critical density, it seems to me that at each measurement, we are either very slightly above or very slightly below.

Hello, Mordred. I believe you're asking what we covered on pages one and two of this thread, aren't you? https://www.scienceforums.net/topic/118858-the-solution-of-the-cosmological-constant-problem/#comments Otherwise I don't know what you're talking about for the moment, can you please specify (here I parallel the evolution of the total critical density with the approach of my previous solution : square root of Planck's energy density)

oops error in the first post : Read [math]H_0^2 c^{-2}[/math] instead of [math]H_0 c^{-2}[/math] Let's consider [math]H_0[/math] the Hubble parameter (or Hubble constant) in [math]s^{-1}[/math]. We want a dimension in [math]L^{-2}[/math] to replace [math]\Lambda_{m^{-2}}[/math]. So we'll write [math]H_0^2 c^{-2}[/math] instead of [math]\Lambda_{m^{-2}}[/math] to get [math] B'=\frac{1}{(8\pi)^2} \hbar (H_0^2/c^2)^2.c[/math], "an energy density of Planck's universe for [math]H_0[/math]". Let's consider [math]\rho_c=\frac{3 c^2 H_0^2}{8\pi G}[/math] the critical density of the universe for [math]H_0[/math]. We have [math] 3 \sqrt{A} \sqrt{B'}=\rho_c[/math] for a quick demonstration we'll use [math]A=\frac{c^7}{G^2 \hbar}=m_p c^2/l_p^3 \text{ } J/m^3[/math]

Hi, In this thread: https://www.scienceforums.net/topic/122453-an-attempt-to-approach-a-notion-of-solubility-in-cosmology-to-explain-the-cosmological-constant/, I proposed a mathematical solution to the cosmological constant problem. However, I have not found a physical explanation. Failing that, I found a generalization of this solution to the whole universe to validate a hypothesis that had been made in this solution In this it is, it seems to me, a confirmation (and perhaps help to understand the problem of the cosmological constant?). The energy density of the quantum vacuum in Planck units is: [math] A=m_pc^2/l_p^3=\hbar(l_p^{-2})^2.c[/math] I, on the other hand, found this unknown hypothetical quantum energy density of cosmological constant : [math]B=\frac{1}{(8\pi)^2}\hbar(\Lambda_{m^{-2})^2.c}[/math] and demonstrated that the cosmological constant [math]C= \sqrt{\hbar(l_p^{-2})^2.c} \sqrt{ \frac{1}{(8\pi)^2} \hbar(\Lambda_{m^{-2 }})^2.c}=\sqrt{A} \sqrt{B}[/math] Let's consider [math]H_0[/math] the Hubble parameter (or Hubble constant) in [math]s^{-1}[/math]. We want a dimension in [math]L^{-2}[/math] to replace [math]\Lambda_{m^{-2}}[/math]. So we'll write [math]H_0 c^{-2}[/math] instead of [math]\Lambda_{m^{-2}}[/math] to get [math] B'=\frac{1}{(8\pi)^2} \hbar (H_0/c^2)^2.c[/math], "an energy density of Planck's universe for [math]H_0[/math]". Let's consider [math]\rho_c=\frac{3 c^2 H_0^2}{8\pi G}[/math] , the critical density of the universe for [math]H_0[/math]. We have [math] 3 \sqrt{A} \sqrt{B'}=\rho_c[/math] The method of dimensional analysis for application in quantum mechanics of general relativity data operates again...

Thank you. I'll look for other cases where we'd have square root energy densities

I have no idea where I'm going.I don't even know if it's applicable, although this encourages me to say yes ( cosmological constant seen as a perfect gas with a negative pressure) : But it's going to be very complicated and the finalization of this project is more than uncertain. I don't know the solubility issues at all and I don't know if scalar and vector aspects are involved in this potential approach. I just want to know if at first glance it seems completely silly or if it's worth trying to find out more about it.

😉

I've got it. It's just [math]\frac{1}{t_p^2\Lambda_{s^{-2}}}[/math] or [math]\frac{1}{l_p^2\Lambda_{m^{-2}}}[/math], whatever you want. The factor is [math]8\pi[/math].

done here : https://www.scienceforums.net/topic/122453-an-attempt-to-approach-a-notion-of-solubility-in-cosmology-to-explain-the-cosmological-constant/

Hi, I have read here under (2.1) that [math]c^5/(G \hbar \Lambda_{s^{-2}}[/math] is a "fundamental pure number" It's the word "fundamental" that questions my mind. What is that fondamental notion please?

Hi, Planck's mass density = [math]\frac{m_p}{l_p^3}=\frac{c^5}{G^2 \hbar} \text{ }\frac{kg}{m^3} [/math] is assumed to be the maximum density in relativity with the mass-energy equivalence of GR, we have: Planck's energy density = [math]A=\frac{m_p c^2}{l_p^3}=\frac{m_p l_p^2}{l_p^3 t_p^2}=\frac{m_p}{l_p t_p^2}=\frac{c^7}{G^2 \hbar} \text{ }\frac{kg}{m s^2} [/math] [math]A = \frac{m_p c^2}{l_p^3}=\hbar c l_p^{-4}\text{ }J/m^3[/math] [math]A =\hbar c (l_p^{-2})^2=\frac{c^7}{G^2 \hbar} \text{ }J/m^3[/math] (1) By dimensional analysis, we make the hypothesis that [math]l_p^{-2}[/math] can be replaced in (1) by [math]\Lambda_{m^{-2}}[/math] to obtain [math]B[/math] a "Planck's energy density of the cosmological constant" and we add a divisor [math]\frac{1}{(8 \pi)^2}[/math] : [math]B = \frac{1}{(8 \pi)^2} \hbar c( \Lambda_{m^{-2}} )^2 \text{ }J/m^3[/math] (2) It turns out that the geometric mean of the squared root of [math]A[/math] and [math]B[/math] is the energy density of the cosmological constant [math]C[/math]. [math]\Large{C=\sqrt{A}\sqrt{B} =\sqrt{\frac{c^7}{G^2 \hbar}} \sqrt{\frac{\hbar c ( \Lambda_{m^{-2}})^2 }{(8 \pi)^2}} \text{ }J/m^3}[/math] [math]\Large{C=\sqrt{A B} =\sqrt{\frac{c^7 \text{ }c \text{ }( \Lambda_{m^{-2}} )^2 \hbar}{(8 \pi)^2 G^2 \hbar} } \text{ }J/m^3} [/math] [math]\Large{C=\frac{c^4 \Lambda_{m^{-2}} }{(8 \pi) G } \text{ }J/m^3}[/math] (3) which is the exact formula for the energy density of the cosmological constant. We must now try to explain the physical reason for this relationship: A square root of energy density could be related to the notion of solubility. Indeed we find the dimension of [math]\sqrt{A}[/math] or [math]\sqrt{B}[/math] is [math]=\sqrt{J/m^3}=J^{1/2}m^{-3/2}[/math] which exists in physics with the Hildebrand solubility parameter (https://en.wikipedia.org/wiki/Hildebrand_solubility_parameter#Definition) which seems to be applicable in the case of perfect gases. [math]A[/math] could "dissolve" in [math]B[/math] with the effect of a constant cosmological constant energy density (= a constant cosmological vacuum energy density) causing an acceleration of expansion Something close to the Hansen solubility parameters (https://en.wikipedia.org/wiki/Hansen_solubility_parameter) in cosmology would be more appropriate? The exact equations of this supposed dissolution effect are yet to be determined if the above makes sense. Finally, we can note for the anecdote, that this presentation is a proposed explanation to the number in 10^122 of the equality (2.1) of this paper (https://royalsocietypublishing.org/doi/full/10.1098/rspa.2007.0370) Indeed: [math]A/C=C/B=\frac{8\pi}{l_p^2 \Lambda_{m^{-2} }} = 8,... * 10 ^{122}[/math]

erase (bad quote)

Hi swantsont Yes ! I saw the word "vacuum" in the penultimate paragraph of the PDF. My level of English is not enough to explain why it appears and how the author relates it to the subject of this article. Can you help me understand by telling me what the connections are between the word an the Planck density in the paper, please? Hi Mordred c^7 comes from the transformation of Planck's density in mass/m^3 into energy density with the multiplication by c^2 (equality (1) = [math]c^5/ (G^2 hbar)[/math] of the pdf of this message : https://www.scienceforums.net/topic/118858-the-solution-of-the-cosmological-constant-problem/?do=findComment&comment=1145564

No, I did not address the problem of the cosmological constant but another question: (Planck density of matter/density of the cosmological constant) in 10^122. I admit that the fact that this number in 10^122 is close to the value in 10^122 of the cosmological constant problem is only a coincidence. I have sketched a physical explanation of the problem that I have solved mathematically, I will come back to it later, I don't have time to develop it now.