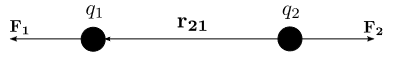stephaneww

uh because [math]c^4/G=F_p[/math] is a component of the energy density of the cosmological constant... link 1 link 2 and that [math]F_p=F_c=k_e (q_p)^2/l_p^2[/math] with [math]F_c[/math] Coulomb force in Planck units except that we need to have a signed charge (but as qp is squared the numerical result is always Fp)

um ok, but how to interpret the presence of these two forces in the energy density of the cosmological constant then ? It escapes me. are there only scalar ?

Okay, thank you very much. I was right to take all these precautions about its validity then and what about this argument please ? Can I say as you that the "field of Planck force" have a directional component. While… ??? The 2 forces (Planck or Coulomb in unit's Planck) are in the energy density of the cosmology constant, no ? of course the cosmological constant have no direction. I'm agree with you on that point

I'll never be able to answer at this point. it's too complicate for me.. The same image is on wkipedia.org at the page Coulomb's law, so I don't know how to consider your answer on this point. Can you light me please ? Can I say as you that the "field of Planck force" have a directional component. While… ??? The 2 forces (Planck or Coulomb in unit's Planck) are in the energy density of the cosmology constant, no ? of course the cosmological constant have no direction. I'm agree with you on that point I'm not sure of the following argument : while searching on search engines I found this document published here which I am unable to say if it is correct and/or if it is very speculative. I only understood this beginning of the conclusion but I don't know if it's valid once again it would seem from this document that Coulomb's force could be applied to particles without charge and regain the FLRW logic

The energy density of the vacuum is affected by the relative permittivity of the vacuum in a given area (local inhomogeneity), which should affect the measurement of the Hubble constant and thus ultimately the determination of the cosmological constant (itself directly a function of the Hubble constant) Did I answer better at this point ?

It is the Planck force, = Coulomb force in Planck units (if you want I put the demonstration) , which applies to the cosmological constant to find the energy density of the cosmological constant , The electromagnetic character is given by two charges of Planck to the square (q1=q2=qp) of the same sign that enter into the calculation of the Coulomb force. source : As a reminder, electromagnetism does not happen by chance in this thread: we have already seen [math]W/m^2[/math] several times. For example, the [math]m_p/t_p^3[/math] which is of the same order of magnitude as the vacuum catastrophe but dimensioned in [math]W/m^2[/math] I hope, without being sure, that I answered your question correctly edit: when we talk about Planck's charge, it means "electromagnetism" somewhere, right?

of course, first, thank you for your reaction edit 2 : I need more time to try to propose a correct answer edit : I don't understand, can you please develop ?

... and since the vacuum of the universe is not completely empty, I let you guess what happens to some methods of measuring the energy density of the vacuum if there is dust or a galaxy in the area. In short, the resulting relative permittivity for each point in the universe will give a different measure and therefore an incorrect value of the cosmological constant. The important thing is therefore to find measurement methods that are not influenced by this phenomenon of relative permittivity of the universe vacuum.

Well, I'm going to move forward in minefields because what I'm trying to understand about electromagnetism is very recent and I'm not sure I've assimilated everything. I hope I'm not saying too much nonsense: with [math]q_1=q_2=q_p= 1.8755459*10^{-18} coulombs \text{ : Planck charge }[/math] source and [math]r=l_p \text{ : Planck length}[/math] source according to Coulomb's law (source) we have the Coulomb force: [math]F_c=k_e\frac{q_1q2}{r^2}=F_p[/math] where [math]F_p[/math] is the Planck force source we have seen that the energy density by volume of the cosmological constant can be written: [math]\epsilon_\Lambda = \frac{F_p \Lambda}{8 \pi}[/math] source as [math]F_c=F_p[/math] it can be safely stated that the volume energy density of the cosmological constant also has an electromagnetic character. In order to apply Coulomb's law to two "quantum particles" of vacuum, it is necessary to assume that they have the same charge to account for the observation, namely accelerated expansion, As soon as time "elapses" the two void charges distant from [math]r=l_p[/math] at the beginning could give way to a new vaccum charge as soon as the two initial charges are far from [math]l_p *2[/math] but this remains to be demonstrated, Moreover, the more "vacuum particles" there will be, the more the amount of energy from the vacuum should, according to this hypothesis, increase, it seems possible by combining Coulomb's strength and the passage of time to explain the expansion of the universe, or even the acceleration of its expansion. All opinions are welcome, although I hope Mordred's opinion is more than welcome.

outch, read : "and validates the measurements [math]H_0=67.4[/math] of Planck's and DES (which are exactly identical) (and not 64.4)

I don't have much time available right now. I have only noticed that the second equality of this post: https://www.scienceforums.net/topic/118858-the-solution-of-the-cosmological-constant-problem/?do=findComment&comment=1117580 could also be written: energy density of the cosmological constant = [math]5,243 *10^{-10}J/m^3=\frac{1.W/m^{2}}{2 \pi c} [/math] in other words, energy density of the cosmological constant could be defined only by [math] c[/math]. which again highlights the importance of the unit W/m^2 (=kg/s^3) in cosmology and validates the measurements [math]H_0=64.4[/math] of Planck's and DES (which are exactly identical) : source : https://www.scienceforums.net/topic/119814-h0licow-new-measurements-of-hubble-constant-highlight-problem/?do=findComment&comment=1113652 Which could extinguish the "tension on the current Hubble constant" and validate the model [math] \Lambda CDM[/math] once again

for the relationship to work correctly in terms of dimensions, it is also necessary to remember that we have: [math]P_p \Lambda / 4 = 1. kg/s^3[/math] and [math]P_p = 3.62831 .kg.m^2/s^3[/math]

Hello. I don't have much free time to continue studying electromagnetism right now. But I'll get back to it as soon as I can. Just a remark on the orders of magnitude. We are often surprised by the small value of the cosmological constant. It is directly linked to Planck's power by the relationship : [math]\Lambda=\frac{4}{P_p}[/math] (remember the relationship of power surface density power expressed in [math]W/m^2[/math] or [math]kg/s^3[/math])

after an exchange with an electromagnetism specialist, this is false: [math]2 \pi[/math] is only a scalar so whatever point in the universe is considered, and if I don't say something stupid again, each point in the universe follows the perimeter of a circle. as : its direction is tangent to the circle so "it is undergoing an acceleration."

Sorry please read in the post https://www.scienceforums.net/topic/118858-the-solution-of-the-cosmological-constant-problem/?do=findComment&comment=1119086 so : [math]\frac{c^4 \Lambda}{8 \pi G}.c .2. \pi=1 W/m^2/[/math] i.e.

Indeed, this presentation is far too difficult for me...

I started to take a closer look.... Beforehand we will assume that [math]\frac{1}{2} W/m^2[/math] is the value that accurately replaces [math]\frac{1}{1,994} W/m^2[/math]. We have the energy density of the cosmological constant =[math]\frac{c^4 \Lambda}{8 \pi G}. J/m^3[/math] Here we have Let's follow the "intensity" link. We find : By following the velocity link, we have : We had found: so : [math]\frac{c^4 \Lambda}{8 \pi G} .c.2.\pi=1. W/m^2[/math] i.e where [math]c[/math] is the speed and [math]2 \pi[/math] is the .. so whatever point in the universe is considered, and if I don't say something stupid again, each point in the universe follows the perimeter of a circle. as : its direction is tangent to the circle so "it is undergoing an acceleration." I don't know if this first approach is correct. If anyone can help me, thank you in advance edit : Um, there may be a problem with the

I'm going back to work to fill in the blanks and also because there's a lot of nonsense… 1* Okay, if I understand correctly, we have two scalar fields' ( I have revised the notion of partial derivative and its modern notation) What can we do with these scalar fields [math]\phi_p \phi[/math] ? I don't understand their usefulness for calculations. ... and I don't know how to use gradients. 2* In this post, https://www.scienceforums.net/topic/118858-the-solution-of-the-cosmological-constant-problem/?do=findComment&comment=1116338 there's been 2 big mistakes. -Indeed, if [math]\Lambda_{s^{-2}}=\Lambda_{m^{-2}}.c^2[/math] then [math](\Lambda_{s^{-2}})^2/c^4=(\Lambda_{m^{-2}})^2[/math] The last line "[math]D=[/math]", of the first post, [math]=B[/math] (demonstration of geometric mean page 2) becomes : [math]D=B=h.(\Lambda_{s^{-2}})^2/c^3/(8∗\pi)^2=6.11∗10−133.kg.m^{−1}.s^{−2}[/math] -the second big error is on the value of [math]H_{p,minimum}[/math] , we do not fond a minimum but only [math]\sqrt{\Lambda_{s^{-2}}}=3.152*10^{-18}.s^{-1}[/math] 3* consequences for this post https://www.scienceforums.net/topic/118858-the-solution-of-the-cosmological-constant-problem/?do=findComment&comment=1116465 [math]R[/math], [math]V[/math], [math]\rho_c[/math] are no longer extreme values, and [math]\Omega_{\Lambda}=\frac{1}{3}[/math]. One might think that the cyclical universe is collapsing, but there is still this indicator that ,perhaps, remains valid : [math]\frac{V.\rho_c.\Omega_{\Lambda}.c.\pi}{V}=\frac{1}{1.994}kg/s^3 \text{ or W/}m^2[/math] [math]=\frac{c^4.\Lambda.c.\pi}{8 . \pi G}=\frac{1}{1.994}kg/s^3[/math] [math]=\frac{F_p.\Lambda.c.\pi}{8 . \pi }=\frac{F_p.\Lambda.c}{8}=\frac{1}{1.994}kg/s^3[/math] But even with that, it is not certain that the universe is cyclical. 4* I agree with you on that point. 5* I still have to learn electromagnetism to try to understand this power surface density...

...And with power of Planck we have : [math]\Lambda=\frac{0.5*8}{c F_p}=1.102422 *10^{-52}m^{-2}[/math] because the unit of 0.5 is [math]kg.s^{-3}[/math] edit : Um, I didn't notice: source : https://en.wikipedia.org/wiki/Planck_force#Other_derivations

Thank you very much. I'm so happy that I put +1 edit : Indeed, if we name X, the value of 1,994 the variation of the cosmological constant from datas, give X in the 3 equations. Second indice, 2pi is the divisor for the Planck reduced constant. edit 2 So [math]\Lambda[/math] would be equal to: [math]\Lambda=0.5/0.5\frac{t_p^2.8 \pi}{h}=1.10242*10^{-52}m^{-2}[/math]

Do you think that if we take 2 instead of 1,994 in post 3 on page 5, we could deduce the exact value, from the Planck units, of the cosmological constant value? I am very tempted to answer "Yes" in the case of a flat universe

However, if we do this simple calculation by dimensional analysis: [math]m_p/t_p^3*2 \pi =8.72*10^{122}.kg/s^{3}[/math] that is the value of the vacuum catastrophe at less than 1% But I don't know what to conclude from that... and if I do, in my spreadsheet: [math]m_p/t_p^3*1.994 \pi =8.72*10^{122}.kg/s^{3}[/math] it is the exact numerical value of the vacuum catastrophe

Yes, generally. Even for Planck's mass?

I don't know if it's a maximum power. I'm not a theorist. What I know about on this subject Planck's force is this : source : https://en.wikipedia.org/wiki/Planck_force#General_relativity But I don't know if it's the same thing for the power of Planck.

I just saw here that: [math] F_p=\frac{c^4 }{G}[/math] [math] P_p=\frac{c^5 }{G}= 3.62831×10^{52} W[/math] … and I have realized the calculation with [math] P_p=c.F_p [/math]