TakenItSeriously

Spoilers please.

Bob and Alice want to share private messages that no one else can read. Using known pseudo random number generators and commutative encryption algorithms that works with a single private key to both encrypt and decrypt messages, provide a logical method that achieves the following: They can use normal text email Trusted third party not required No keys need to be shared Secure at least to the level of perfect encryption. No one else can modify their messages without their knowing it No one else can block their messages without their knowing it No tricks or gimmicks Solution is apparently real AFAIK, though I've never been able to have it vetted it. hints Cross posted in the twoplustwo puzzles forum under user name TakenItEasy (not TakenItSeriously) http://forumserver.twoplustwo.com/59/puzzles-other-games/testing-my-constitutional-rights-1666637/#post52202148

I've seen this before, its a neat illusion. If you tie the helium balloon to the floor of a van and accelerate foward, then the balloon leans forward instead of backwards making it behave like negative mass. Why it happens is helium is lighter than air. So the heavier air in the car is what is falling towards the back of the car and the lihter balloon is floating forward over the air. The illusion is created by what we see (balloon) being lighter than what we don't see (air) which is intuitively not usually the case.

Memory being stored as a parallel process as opposed to a serial process is completely consistant with my own experiences with my learning disability that involved poor short term/working memory with connected reading and auditory comprehension issues effecting my ability to learn from either text book or lecture, though learning through other methods worked much better. What I discovered in my case was that if any single piece of information is missing for some reason in the learning process, then I could understand nothing after that piece at least for the rest of the chapter. This implied that the long term and short term process must both be working in parallel, and here's why: Consider the following: Lets assume that a chapter in a math or science textbook is 10 paragraphs long and the following is true Understanding paragraph 2 requires remembering/understanding paragraph 1. Understanding paragraph 3 requires remembering/understanding at least paragraph 2. Understanding Paragraph 4 requires remembering/understanding at least paragraph 3. ... and so on. Therefore, we can assume that understanding paragraph 10 requires remembering and understanding all 9 paragraphs that came before, which I would presume exceeds short term memory. To see that this is true, consider what happens if you remove any single paragraph from your memory, then there is a chain that is broken and none of the rest could be understood, which was exactly what happened in my case every time. So esentially, if I had a question at the beginnig of a lechture it had to wait till the end of the lecture, so I never understood anything after the question. I could also verify this hypothesis (to myself which was all I needed) through alternate learning experiences which was most dramiticly demonstrated by one on one learning with one example occurring after my standard education and one before. My education was beset with other problems that I don't discuss here, but the troubles I discussed above were definitely real, for any advanced course material. When working as a PCB designer I wanted to learn electrical engineering, though Id never taken a singe EE class before. I was given the opportunity when I designed a PCB for a Stanford EE professor who liked to monitor the design process which wasn't a problem for me because it gave me the opportunity to pepper him with questions. After the first few questions, he got the drift and just started teaching me from the beginning going through his lechtures while I designed his board which didnt require any focus on my part as design had long since become an automatic process for me. He was a very good teacher at the end of his career and about to retire as I later found out. Since I could asked questions as we went, I could easily grasp everything. The desiign took about 16 hours over two days, but half way through the second day he stopped. When I asked why, he said that was all there was and he'd covered all three semesters of material that he taught, and he said I had a better grasp of the material than any of his graduate students. While I wouldnt have been able to recall much of that information due to a serious overload of information at the time and my problems with short term memory, I'm pretty sure it was still all captured by long my term memory which seems to have a different recall mechanism based on working on problems that required the information which I just seemed to know later on and must have mostly come from that session. Another example occurred at the beginning of my education. I learned QM, SR, GR, and Astronomy sans the math at the age 7-8 because of my own intense interest and two older brothers who both majored in the sciences and were willing to teach me taking less than a year. I came away from that experience with a very strong understanding of those subjects, though odds and ends were missing, such as Quantum spin, intrinsic magnetic moments, or the Lorentz transform which I learned later in school but the vast majority of it was just review, and several times my grasp of the subject matter was better than the teachers. Learning through the internet also got me around those hurdles by having access to multiple resources but also comes with it's own disadvantages such as learning out of order (massive headache), missing subject matter that you might not know exists, inconsistancy of sourcees, etc.

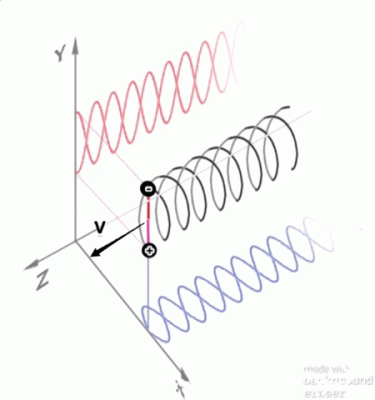
We can try to think of it logically, but I tend to take logic to details that most are not comfortable with, so it may not be much help. let's define the following: A ≡ entanglement B ≡ superposition states C ≡ imaginary hand ranges (as if they were in a suoerposition state) domains: X ≡ the Quantum domain Y ≡ the Human domain Z ≡ a virtual domain of Y Let's assume the following: A must follow as a consequence of somethings existence in the state of B within domain X. A is not possible within domain Y. We have a problem C in domain Y which requires imaging it in a state of B in order to begin solving for C. Then solving C 100% becomes problematical at the point of where A must be the result because A cannot be the result in domain Y. Next consider that even if we use a virtual domain, Z, to solve C. then problem C would still seem to be unsolvable as long as we continue to treat C as something that follows the Laws of Y. That's when I began to experience the persistant bug in the creation of my poker simulator when implementing Range Removal which is intended to capture 100% of possible information. The problem was that since it was a simmulation I treated everything as being very literal. The, only solution seemed to involve going backwards in time and instantaneous updates in multiple locations which is not the typical kind of logic error I was accustomed to (outside of QM that is). The trick was to stop being so literal when it came to hand ranges and divide the everything into a real state and an imaginary state. This allowed me to take liberties in the program in order to solve C retroactively which got me to around 99% accuracy (second order), though I haven't given up on a 100% solution which is possible using a model I've developed for QM involving loops which I won't go into here. Figure 1: A dual helix model. Tap to animate.

I don't believe I ever contradicted myself. the whole point was that I ran into the same kind of entanglement problem which was preventing capturing 100% of the information, in a virtual environment, though using work arounds, I was able to capture around 99% of it.

Which I've stated myself many times already. The weirdness doesn't show up until you try to account for all information and then it doesnt actually happen, it only prevents the math from working properly.

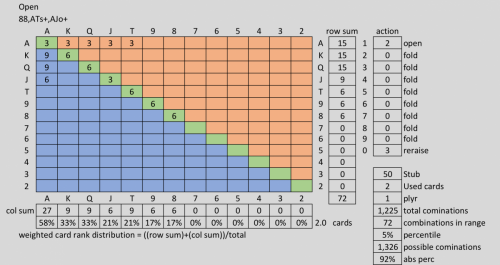
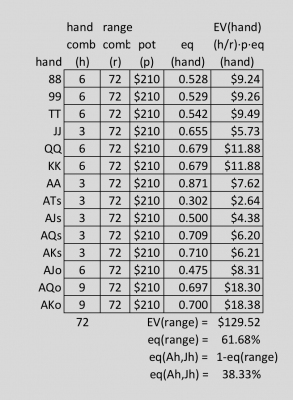
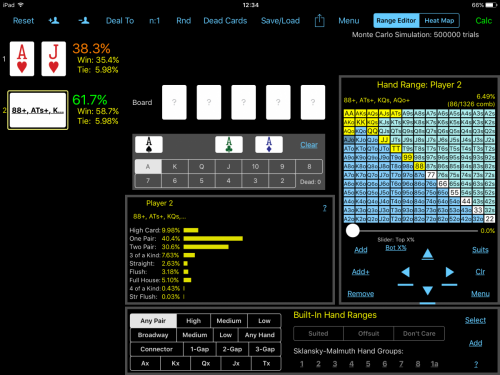
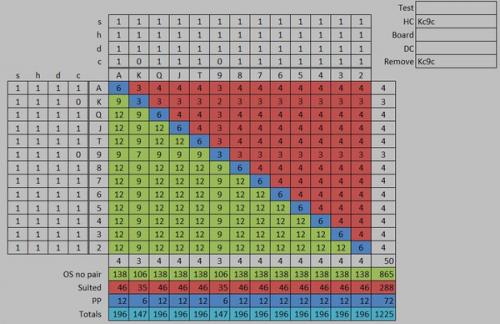
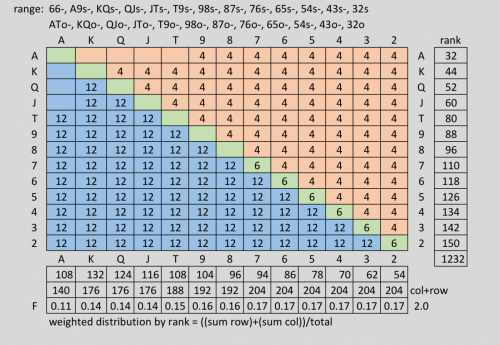
You have AJs and are facing a player who has 3 Bet a shortstack all-in from the BB for a pot sized raise in a cash game. All other players have folded. You have a long history with this player and you know his range is: 88+, ATs AJo Your getting 2:1 on a call. Should you call? To know whether you're getting the right odds to call you need to run a hand vs range equity calculation like the one shown above. [edited to highlite the following:] Another words your decision is based on your hand vs his range of hands with the 2:1 pot odds. This example of a poker hand provides zero evidence for your assertions. What does calling or not calling an allin 3bet from the BB while having AJs and putting the guy on some range while having 2:1 odds have to do with quantum mechanical superposition? Its a rhetorical question - it has zero correlation, please dont even bother to explain and get youreself deeper into the rabit hole of nonsense. Please quote the part that doesn't make sense to you. Unfortunately the math that treats an entire range of hands simultaniously as a single entity is integrated in poker calculators as part of the Monti-Carlo simmulation so I am limited as to how much can be revealed through math alone. What I can show is how the range can be broken down into its component hands and then allow each hand equity to be calculated through simmulation individually. At that point I can show how to calculate the EV of each hand individually and then recombine them all as a weighted average which should produce the same results as those given by the poker calculator. In order to fully understand this process, I'll provide some explanations about some concepts used in poker first. Equity calculations: EV or Expected Value is calculated using "equity calculations" which are intended to analyze a single decision in order to determine the most profitable choice. Equity stands for the percentage of times you are expected to win the hand when all-in. Expected Value is the long term weighted average of the results, in terms of cash value, over time. The decision in this case is wether it's better to call or fold to an all-in pre-flop bet. The example: Blinds $5/$10, $5 rake, 10 player, NLH Villain is on the button playing a short stack of $100. You Open raise to $30 one seat before the buttton with [Ah, Jh]. Button shoves all-in and both blinds fold. Pot is $140 and it's $70 to call so your getting 2:1 odds for the call. You put the button on a range of: (88+, ATs+, AJo+) and, for the sake of discussion, let's assume that range is accurate. Hero's hand: AJs Villain's range: 88+, ATs, AJo We are comparing the equity of our hand vs the equity of all hands in villains range simultaniously which is the analogy in a nutshell. Using a poker calculator we get the following results: eq(AJs) = 38.3% eq(88+, ATs, AJo) = 61.7% Pot = $140 [+call] to call = $70 EV(call) call and win = $140·38.3% = $53.62 call and lose = $70·61.7% = -$43.19 ⇒ EV(call) = $10.43 vs EV(fold) = 0 So we can see that even though you're a significant underdog vs villains range, the favorable pot odds makes you pot committed to a call. Note that if the opponent happens to be ahead after you call, that doesn't mean that the call was a mistake. It's merely a natural consequence of making decisions vs a range of hands (when we're sometimes ahead and sometimes behind) in situations when the information isn't sufficient to defining the opponents hand to any better resolution, therefore we must make the decision that is the most correct for all possible outcomes of that range. I like to think of this as the Many Worlds Interpretation of Poker. Since the math showing how those sumultanious results are calculated is done mostly within poker calculators that use Monti-Carlo simmulations. I am a little handcuffed when it comes to showing 100% of the math because of the simmulation component. I will show how the problem can be manually broken down to be treated as individual hands and then recombined in order to get the same result that the poker calculator reached when treating the entire range as a single entity, vs a single hand. I will start by removing the cards in our hand from the deck, since, when they are in our hand, they can't show up anywhere else. Next, I will break down the opponents range into their component hands while taking their odds of occurrance into account using combinatorics. In quantum computing, this would be referred to as the qubit's coefficient term. Removing the Ah and Jh from the deck state necessarily means that the opponents range will undergo many significant changes despite the opponent doing nothing himself that could trigger those changes. This concept is important when getting into Range Removal effects and can be seen using a hand matrix. The Hand Matrix: Figure 1: The poker Hand Matrix is a basic tool use in poker as well as most poker tools, mostly for representing 2 card combinations as a players hand in Texas Holdem. The blue section represents all unpaired offsuit combinations such as [AcKd] The orange section is for unpaired suited hands such as [QdJd] The green is for paired hands such as [TcTh] The numbers represent the number of ways 2 cards can combine to make the hand. For example a pair can be combined in six ways: [Tc,Td] [Tc,Th] [Tc,Ts] [Td,Th] [Td,Ts] [Th,Ts] Notice that these regions can be somewhat misleading due to the fact that off suite and suited hands appear to be symmetrical within the matrix, but there are actually 3X as many off suited hands as suited hands. It's also important to understand that the combinations shown are based on dealing from a complete and random deck state. Once information from observing cards, hands, or ranges are known, then the distribution of combinations instantly changes, even though we may not realize it since the actual range never seems to change only the odds that they are based upon changes. Card Removal Figure 2: Card Removal Matrix. When we assume a completely random deck state, then all possible range combinations are all evenly distributed within their combination types, ie. all unpaired off suit combos can be created 12 ways, All suited combos in 4 ways and their are 6 ways to make a pair. Hand Ranges At the beginning of a hand we must imagine an opponents hand as if they were all reasonable possible hands rather than making futile guesses about an single hand that he may be playing. Their are 1326 possible hand combinations that can make 169 possible hands. Therefore at the beginning of a hand, the only way to make meaningful decisions is to treat opponents hands as a range of all possible hands simultaniously. Even to the extent that we solve them as single hand vs a single range as a lumped sum. This is mostly done using computer simulations. Therefore, the existance of the analogy is true because that's how we imagine hand ranges must exist in order to apply the math efficiently as one lumped entity, but its much easier to do this in conjunction with computer simmulation. It's a useful analogy despite ranges being an imaginary concept because we still must treat the imaginary ranges as if they are real and still must use math and logic based on assuming a real range state which had always been true at least up untill now. Note, When dealing with Range Removal and treating ranges as if they were real when programming a vrtual reality poker simulation. I discovered that their are limits to how far we can treat ranges as being real brfore the math stops making sense. Figure 3: The hand range of 88+, ATs+, AJo+ is shown here. While poker equity calculators use Monty-Carlo simulations to treat all hands in a range as one. I cant show the math completely. What I can show is how we can break down the range into individual hands and compare the net results with those provided by the calculator. Total combos in range = 6+6+6+3+6+6+3+3+3+3+3+6+9+9 = 72 Each hand combo can then be broken down as a percentage of the range AKs, AQs, AJs, ATs+: (3/72) AAp, JJp: (3/72) KKp, QQp, TTp, 99p, 88p: (6/72) AKo, AQo, AJo+: (9/72) The equity for each hand vs [Ah, Jh] must be calculated individually: eq(88) = 0.528 eq(99) = 0.529 eq(TT) = 0.542 eq(JJ) = 0.655 eq(QQ) = 0.679 eq(KK) = 0.679 eq(AA) = 0.871 eq(ATs) = 0.302 eq(AJs) = 0.500 eq(AQs) = 0.709 eq(AKs) = 0.710 eq(AJo) = 0.475 eq(AQo) = 0.697 eq(AKo) = 0.700 The Expected Value or EV for each hand can be calculated using the equation below: EV(hand) = (h/r)·p·eq(hand) Where: EV = Expected Value in cash h ≡ number of card combinations that create the hand r ≡ number of card combinations in the range p ≡ the size of the pot after a call eq(hand) ≡ equity function of a hand v hand or hand v range. Figure 4:: Breaking a hand range down into its component hands. Results Hand vs range results using PokerCruncher App for the iPad: PokerCruncher-Advanced-iPad V.9.5.1 (Equity, Win, Tie) Player 1: 38.3% 31.7% 13.3% [AhJh] Player 2: 61.7% 55.0% 13.3% {88+, ATs+, AJo+} Board: [? ? ? ? ?] Deal To: River Dead Cards: {} Monte Carlo Simulation: 500000 trials Note that this is generally as far as probability analysis or computers could take us ordinarily. However, It is important to note that this calculation is not entirely accurate unless it's for a heads up game. For game scenarios that include any players folding their hands, there is still quite a bit of information left unaccounted for since folded hands are ignored or treated as random cards that assumes players would fold AA pre-flop, which would never be realistic except under extreme trournament situations such as satelite bubbles. However, until recently, it was the best that we could do with what we currently understand.

You have AJs and are facing a player who has 3 Bet a shortstack all-in from the BB for a pot sized raise in a cash game. All other players have folded. You have a long history with this player and you know his range is: 88+, ATs AJo Your getting 2:1 on a call. Should you call? To know whether you're getting the right odds to call you need to run a hand vs range equity calculation like the one shown above. Another words your decision is based on your hand vs his range of hands with the 2:1 pot odds. Actually, I'm pretty sure the method is pretty much the same, but of course the details are different.

I covered that here: So your saying that we cannot imagine hand ranges where all hands are treated as if they are simultaniously all true when making equity calculations?

You should read the post before replying.

Again, the analogy is not the strategy you may use to determine a range, the analogy is the range itself and how the range must be treated by a player assuming the player knows how to mathematically treat a hand range using equity calculations and other maths. You may argue the validity of what I am claiming, but you may not change what I am actually proposing, which is what you seem to be trying to do. Never the less, most poker calculators can calculate the all-in equity of a hand vs a range of hands because it calculates the average winnings as if the player was playing an opponent who is holding all hands in his range at the same time, and find the average net outcome after calculating for thousands or perhaps millions of possible outcomes. Iinside the calculator, the algorythims must have used algorythms pretty much identical to the way that quantum computers work, only using standard bits instead of qubits. Thats why they can take so long when calculating for large ranges or multiple ranges. What a poker calculator could not do at least until I found a solution a few years back was to account for the information that was lost in the muck and instead treated that information as if it never left the deck assuming all unseen cards are still part of the random deck state. It was when I was trying to find a solution to recover this missing information that I encountered the problem where a quantum entanglement like effect was creating bugs in the algorythms that didnt seem possible to fix at least as long as I treated ranges as real things that obeyed cause and effect or didnt allow quantum teleportation. So, no I did not witness any quantum effects, ever I only experienced persistent bugs in the poker simulator I was developing that didnt seem to have a propper fix because it seemed to require an instantaneous and simultaneous redistributiond of all ranges, which I believe QM calls normalization, every time new information was introduced into the game state. It's not exactly the perfect analog, few things are, but it represented the essence of how some effects especially when measuring different spin states to work. Once ranges became so narrow such as an opponent representing only KK or AA, so that I can safely fold KK that is way behind 6 out of seven times and a tie 1 out of seven times that the analogy of measuring the same spin angle would seem valid. It definitely wasnt the weak analogies that science documentaries use all the time that often spreads as much disinformation as information. I imagine a game could be concocted that used cards that perfectly fit the analogy for creating a mathematically proper analog, though it would make for a pretty dumb game and be just as weird as the QM effect itself so I don't see the point. Like playing go fish with three cards face down in front of both players then asking if an opponent had any black queens and if he happened to turn over a black queen then a red queen would be revealed in front of you. In any case, it wasn't until I stopped treating hand ranges as real things that I could finally find a work arounds that provided a close estimate to a solution and applied it retroactively with pretty good results.

I think you're both missing the point of what I am claiming to be analogous to QM, which is not poker strategy in its entirety, or the physical state of the cards or deck of cards. The analogy lies in the hand range analysis aspect of poker which is an entirely conceptual or an imagined state of existence that doesn't ever actually exist. The only things that truely exist are the actual cards our opponent is playing, but without any way of knowing what those are definitively at the beginning of play without cheating, we are forced to imagine them as a concoction of all reasonably possible hands. Therefore they are analogous to superposition states in a sense because that is how we define them to be in the first place, but only in our minds. Effectively, we define hand ranges to be a range of all possible hands at once, just as superposition states are all possible states of a fundamental particle at once. In fact you could even say that poker calculators that run Monty-Carlo simulations of hand vs range is a realization of the Many Worlds Interpretation of Quantum Mechanics. Because it runs through all permutations of what an opponent may be holding as well as permutations of the deck state for all possible future outcomes and combines them all together in a giant equity calculation to show whats the most profitable play given the same scenario played over an infinite number of times. (not literally an infinite number, its just an expression that's often used.) I should also add, that just based on a scale of numbers, these concepts are not on as different a level as you might think. Not that the following example is a direct comparison by any means, but it should give us more to think about when trying to imagine things that are outside of what our imaginations are used to dealing with. If we were to consider that the Pauli Exclusion Principle required every electron to have an infinitessimally unique orbital state or electrons would be constantly colliding into each other. While I'm not sure how that interplays with QM superposition states. That means that electrons must have a very large number of permutations somehow encoded into them to accomidate the number of every electron in the universe which would seem to be a pretty mind blowing number. However, now compare the number of electrons in the universe to the number of possible deck states there are (unique ways the deck may be shuffled). Before looking it up, I'm guessing that the number of deck states is much larger. Edit to add: After looking it up, I was wrong, current estimates have the number of electrons on the order of 1E80 while the number of deck states are only on the order of 8E67.

The following is not true - but it gives an idea. You have two cards A and B - one is an Ace the other a King; you do not know which is which. With classical cards you could say that measure card A by pairing with another known card and then turning the unknown over. So if we measure card A by pairing with a Queen and measure card B by pairing with another Queen. If you get Ace Queen with card A you must get King Queen with card B. This would be the same if the Ace and King were in superposition But if we measure card A and card B DIFFERENTLY - ie we measure card A with a Queen and Card B with a new Ace. Then with the classical measuring that if you get Ace Queen with card A then ALWAYS you will get King Ace. But with a superposition and with a different measurement of the two entangled particles (this is the equivalent of measuring on different axes in Bell Experiment) if you got Ace Queen with card A there would be a possibility that with card B you would get King Ace and also a possibility you would get Ace Ace I'll concede that my statement was prematurly stated and not exactly how I should have expressed it. Also, what I had intended to say isn't really that important. However, I think I understand where your going with this analogy which, If I'm right could serve a very useful purpose where I think we could have some common understanding of one of the more confusing aspects of entanglement, that I would have had trouble explaining myself, while recognizing it in your example of showing the relavance of the hidden information of entanglement. Correct me if I'm wrong but It seems like it was intended to show that the mathematical treatment of results when two observers measuring the same entangled spin angle is actually mathematically equivalent to two measurements of a single spin property as represented by the Queen And that's mathematically different when measuring different spin angles that sometimes represent two different spin states represented by the Queen or Ace. It wouldn't matter that neither observer knew when their measurements coincided, only that they know that they would a third of the time. Is that the gist of what you were saying? BTW, I finally got around to translating that quote. I do agree that QM can be extremely confusing. However, I think that's all the more reason for looking at it through an appropriate analogy. Once you realise that most of it is just probability, then QM becomes much easier to understand. . .. .

The relavent correlation under discussion is that each observation seems to have an instantanious effect on all entangled objects. Also to say that probability in general is only one thing it has in common is not a fair statement like saying two things have calculous in common. Its the details of how probability is treated equivalently to both. for example some details are that superposition states are discrete states of existance the same as hand combinations are descrete combinations . or that any lesson in quantum computers could be translated just about word for word into a lesson in equity calculations. There is more than enough to learn from when comparing two, either as a teaching aid or as a tool for learning some of the aspects of QM, that we may not understand that well yet. For instance that entanglement seems to be a consequence of the laws of conservation.

Whether a particle has no specific state before one decides to look seems pretty irrelevant. However if you could give an example of how it becomes relevant, Id be open to considering it. I agree that Its the ability to make the observation that is important which is the whole point behind the equivalence principle. So In a poker game that's played online where live tells are not evident and a player cannot physically see the hand except through the intended methods of player actions is all that is important in the analogy. What I meant about the complete accounting of information is that all available information has been accounted for, not necessarily when or how you observe the information. That is why this effect has never been associated to poker before now. Because previously, with probability, too much information was left unaccounted for in the muck.

Effectively, the opponents hand does not have definitive value to the player except through the information that he is able to observe. measuring spin, speed, momentum, polarization, or any other complementary property is not the important aspects that cause entanglement. True they are not technically proper analogies which would mean that they were mathematically identical. However they are analogous in their cause/effect mechanism. And the mechanism of the poker analogy seems to indicate that entanglement is created by conservation laws and the complete accounting of information in a system. Anything that is complex in it's understanding can be explained in a simple way once its understood well enough.

Actually, I'm pretty sure that Wave functions can be translated into probability densitty curves, as long as their is a polar aspect to the problem which is not the case here, but it is the case in another post I had made about bells inequalities. http://www.scienceforums.net/topic/103544-proof-that-bells-inequalities-are-equal/?p=974405 In that post I had used aspects of Range Removal for calculating the bias in the distribution of spin combinations for detectors at 0, 60 and 90 degrees. in that example I believe the probability density curve turns out to being equivalent to the wave function results.

Actually the complexity of quantum entanglement is about as simple as it gets. alice measures spin up in the y axes then Bob must measure spin down in the y axes. whats so complicated about that? The difficult part is in understanding how Bobs particle knows to be spin down the instant that alice measures spin up. Quantum weirdness just means it is not well understood, but not necessarily complicated, IMO. stack sizes are not relavent in the examples as they were intended. In fact neither does strategy play a roll, only that the ranges are definitive such as with poker bots and that ranges always includes the actual hand. If you like assume every stack was sufficient to make pot sized raises and sufficient to being priced out vs an all in. BTW, polarized ranges into a four way action pot? from the first four players in a ten handed game??? What kind of poker do you play.?

I think I may have oversimplified the problem to the point where the concept that I was trying to illustrate was lost. The analogy for quantum entanglement has to do with the fact that information about one particle has an instant effect on the other particle based on property A is read by Alice therefore Property A cannot be read Bob. In the poker analogy case their is a similar effect with ranges that are changed with each new range introduced. The easiest way to explain it is when each new range is smaller than the previous ranges ie. each player raises the others. Let's begin again with player1 opening with the same standard raise with the same range: 88+, ATs+, AJo+ which means that his hand weighting would look like like the following assuming a full and random deck. 0.7 Aces 0.3 Kings 0.3 Queens 0.3 Jacks 0.2 Tens 0.1 Nines 0.1 Eights = 2 cards Assume player2 raises with an even tighter range of QQ+, AKo, AKs where .825 Aces .825 Kings .350 Queens = 2 cards Then introducing player2's range would an instantanious impact on the weighted distribution of Player1's range to suddenly be much less likely to contain Aces or Kings. and much more likely to contain smaller pocket pairs. lets then assume Player3 reraises with a range of KK+ 1.0 Aces 1.0 Kings for a weighted average. (2 aces 1/2 the time and 2 kings 1/2 the time.) Again both player1's distribution and player2's distribution of cards both must be adjusted instantaneously. Finally assume player 4 raises all in which he can only do with aces only and action folds around to player1 who also goes all in with aces. now all ranges have become nearly definitive where we know that Player3 must have KK only and player 2 has QQ 6 times in 7 and KK once in 7 and clearly both must now fold. The point is that each time new information is introduced then the previous ranges must be redifined to adjust for the new information. And in theory, the information is transferred instantaniously. As I said, their was no paradox and these were just elementary school teachers, but to be fair try converting a simple equation of say:20-15+13-10+2=10 But using the negative counts each time and youll find it's not easy to encorporate negative counts into the arithmetic. I'm sure their are riddles that intuitively seem to create paradoxes, though they are not, which are based on negative counting. I just can't recall any of them.

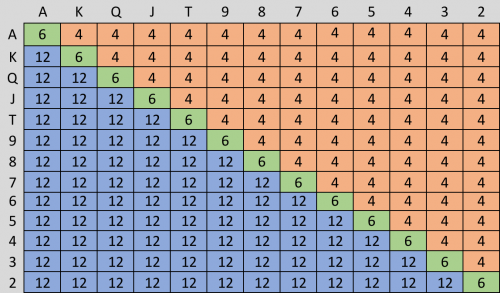
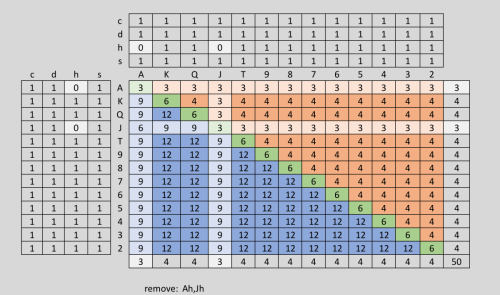
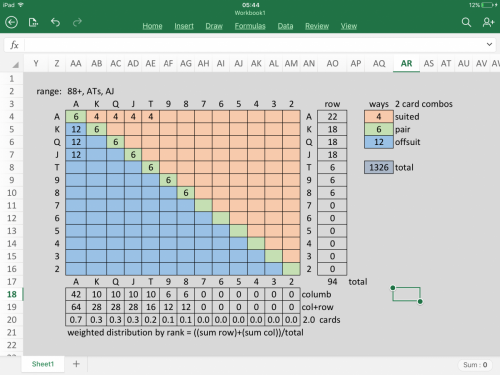
The standard analogy of poker to QM: In QM fundamental particles exist in a superposition state in which all discrete combinations of properties exist at once. In poker, players must treat their opponents hand as an imaginary range of all possible hand combinations of hands that fit with the players past actions. Probability Theory: In poker, probability theory is limited in its accuracy due to it's inability to account for information lost in the muck when players hands are folded. This was something that probability theory had assumed to be too complex to be calculate. A few years back, I had managed to account for this missing information based on a simple idea I had first applied in the first grade, which had created quite a stir at the time. The idea was that when the physical counting of objects was involved for problems of arithmetic such as taking 15 blocks away from a pile of 20 blocks, I had reasoned that it was faster to count five blocks and just grab what was remaining which allowed one to take far less time counting blocks. My solution was apparently a novel approach and when teachers tried to apply math to account for the practice, the math seemed to create a paradox. A fact that I argued against with teachers at the time. Really it only created an intuitive mathematical error caused by how we inntuitively cound objects in the positive domain and not the negative domain, but evidently riddles were apparently created based on this incident that were thought to demonstrate the paradox for a brief time. I applied the same practice of counting the negative of a range in order to retrieve the information that was previously lost in the muck. Another words a folding range was simply the negative of the range of hands that were played. I called it hidden information because the human brain is not trained to think in the negative and so we never even knew that such information even existed. Using negative ranges was the initial basis I used for solving the problem of capturing 100% of all attainable information from a system which in this case was a poker simulator that I had created in Excel. While playing poker against human players involves free will, the problem could be too complex to solve, but I wanted to find a baseline using pokerbots within a poker simulator which I was also developing at the time. Poker-bots could simulate the actions of humans, but still have completely determinant hand ranges, and hand ranges were the key to the solution. An example of a hand range may be the following: In a ten handed game of Texas Holdem, a player or a bot, might open raise when first to act with a tight range of the top 8% of possible hands such as: 88+, ATs+, AJo+. That range could then be reduced to an average weighted distribution of card ranks within two cards as demonstrated below using a hand matrix in Excel: Figure 1: A Hand Range Matrix used for calculating the distribution of card ranks in a range using Excel. Note that the numbers within the matrix represent the number of ways that a pocket pair, unpaired suited hand, or unpaired unsuited hand are created in ratios of 6, 4, & 12 ways respectively. Another words, after the raise but before looking at your own two cards, the remaining cards in the deck would, on average, contain: 3.3 Aces 3.7 Kings 3.7 Queens 3.7 Jacks 3.8 Tens 3.9 Nines 3.9 Eights 4.0 Sevens 4.0 Sixes 4.0 Fives 4.0 Fours 4.0 Threes 4.0 Twos Adding up to 50 cards. If the player in first position had instead folded in that position, assuming that they didn't have a calling range (which is standard), then the average distribution of the remaining cards would be quite a bit different: Figure 2: A hand matrix showing rresults for a folded hand in the same position results the remaining stub being: 3.89 Aces 3.86 Kings 3.86 Queens 3.86 Jacks 3.85 Tens 3.84 Nines 3.84 Eights 3.83 Sevens 3.83 Sixes 3.83 Fives 3.83 Fours 3.83 Threes 3.82 Twos Again adding up to 50 cards. Therefore it seems like all that needs to be done is to reduce every player range down to two weighted cards and remove them from the deck which should produce the average weighted distribution of the stub containing 32 cards, right? Unfortunately it's not that simple once we try to account for more than one range. One reason is that the combinatorics functions require us to use only integers, so to accomidate the percentages of weighted averages, I had to figure out a new method for approximating the combin function using rational numbers. More importantly the laws of conservation tells us that for every new range that we introduce, their must be an immediate adjustment made for all past ranges as well as the distribution of the remaining deck influencing future ranges due to the finite number of cards being fixed at 52. That seemed to imply that information had to travel in a loop both forwards and backwards in time, or to put it another way, it required an instantanious transfer of new information to all player hand ranges already defined or yet to be defined, similar to how entanglement works, thus making it seem like the problem could not be solved. I was finally able to find a solution (mostly) when I eventually realized that hand ranges weren't real. They were only how we must imagine our opponents hand where as the real hand had always been the same two cards. Once I realized this, I was free to figure out a method that could automatically redistribute ranges based on all existing ranges simultanoiusly which seemed to work extremely well for the one trial I had time to test with a Monti-Carlo simulation before all of my projects were lost due to hackers. This theoretically would have allowed me to make calculations far more accurately then ever before based on far more accurate information in the stub. Before probability calculations assumed that future cards were always dealt from a random deck of 52 or 50 random cards regardless of 20 cards already in play, we could now assume that they were dealt from a stub of 32 cards with a biased distribution of hand ranks based on weighted averages of all of the ranges involved. The link below is where I announced the solution (but not the discovery of the imaginary QM like effect which I assumed would be too dificult for people to easily accept). http://forumserver.twoplustwo.com/15/poker-theory/card-removal-card-bunching-solved-1418266/ Again, while the quantum effect modeled is real in terms of conservation of information, it is based on imaginary ranges that only exist in our imaginations. Also, I believe the limitations of those quantum like effects in the macroscopic domain, does not violate any of the Laws of nature but I believe that it does set limits on how accurately we may calculate our predictions using probability theory, when attempting to capture 100% of available information, which never the less is far more accurate than we can currently calculate using probability theory alone and far faster than we can calculate using Monti-Carlo methods. If I am ever able to recreate or recover the project, I hope to know more about it at that time. Below are, pics that were taken of the origional project showing the Range Removal section and does not even include the poker simulator section or the VBA code involved in the poker simulation or poker bot algorithms. Figure 3: Matrix used for removal of known cards shown above. Figure 4: Section responsible for calculating Range Removal effects. Note that the known card removal matrix is the matrix shown in the top right corner of the picture.

This was qauestion about an observation of a sudden behavior shift that that I thought might be explained by an IQ shift and wanted to know if there was any research to support or deny it. Most but not all of the replies seem to have each, individually imagined something completely different and each started to attack based on IDK what and I dont want to know. So Ill just let it drop here and leave this awkward mess alone, but you shouldn't read anything into that. Edit to add that i missed the last few posts befor this one which included an analysis that seemed spot on.

I've been noticing that the people seem to be much less reasonable in their thinking these days, as compared to periods like 10-20 years in the past. I also happened to come accross a couple of articles about studies and/or standard tests that appear to agree. The only hypothesis I saw given in the articles was that it has been suggested by a few that weve reached our evolutionary peak which is about as random a reason for an excuse some concern as I can think. Other examples that would seem like clear indicators to me are the divergence of peopleles opinions most evident in politics, but also across all sectirs it seems. Theres even a trend to elect dumber politicians who have replaced intelectuals and weve lost the ability to compromise for the greater good and we would rather sacrifice the greater good just to hurt the other party. I've always been a moderate so about as close to neutral as you could be I imagine with no party affiliation and hadn't followed politics as closely as I ahould have, but these days being a moderate seems to mean that everyones both sides are taking stupid positions about half the time based only on party lines and I can't even begin to discern which is the lesser of two evils I dont want this to be a political discussion but its just the most striking evidence and the greatest cause for concern. How can a government survive when the shift is towards extremism. That's a recipe for eventual collapse which should cause everyone to worry if they aren't already too worried about their own governments.. Everything that was unthinkable 20 years ago seems to be the standard today. Has anyone done any research that looks at automation, expert systems, or AI trends to be a cause. As an interested observer, I would speculate that technology could be the best candidate. since the effect seems to be world wide. Perhaps it has become too easy where we don't need to think nearly as much as we used to and just like the body, if you don't use it you loose it. It's recently been accepted that intelligence can vary over time, I haven't read much about the details. But for the body we understand that and at least make some effort to compensate through excercise. But I'm sure that most are still under the impression that intelligence is static. Even knowing differently probably hasn't motivated many to do anything about it.

Im not sure where the cards changeing value trick came into it but no, I dont think that's true at all. Clearly the poker reference wiffed. While its relevant I should have posted under its won topic as a poker analogy to QM or quantum computing so that it would attract only those with the shared interests. poker discussion at the level I was representing is very deep and non-intuitive without the proper prerequisites of understanding first. I'll continue with the restatement instead.

oops sorry