TakenItSeriously

Thanks for the feedback. Since my skills are strongly biassed towards logic but not necessarily math (depending on how you think about the two) providing a proper mathematical explanation could be a huge benefit towards a more widely based understanding, which I would have a very difficult time deriving completely on my own.

You’re right. I thought that there was a bounded symmetry within regions related to Mersenne and perfect numbers where the number of odd and even numbers must eventually be equal. While that’s true for the numbers in the vertical direction, it’s not necessarily true for the series in the x direction. It’s not a valid proof as I’ve stated it. It does reveal some interesting relationships though like any Mersenne number will begin with an odd series equal to the exponential. while perfect squares, of course, converge to 1 in the same number of series. Also it seems like there should be an exponential function that could predict the point where the series drops below n, based on a persistant pattern I see that seems to relate to an exponential curve.

Your quoting my post out of context.

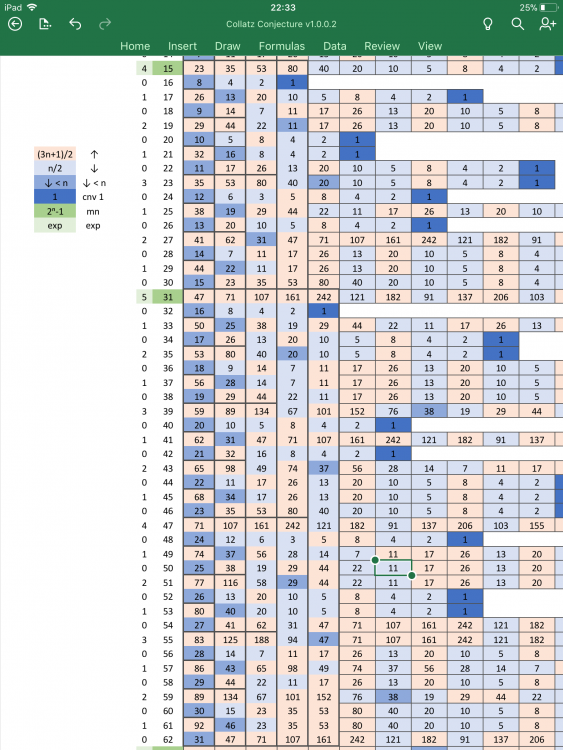
Edit to add: I forgot to mention that the distribution of numbers that expand or contract are distributed evenly by the periodicity of prime factors: two and three, which produces a random like distribution similar to prime number distributions, which are infact goverened by growing cyclical distributions between Mersenne Numbers thereby forcing the -EV long term average assertion to be true. Figure 1: Reveals the cyclical pattern based on 2n where for each column the repeating cycle doubles in size.

Ahh, thanks for the tip. I’ve often wondered why Cosmology chose the Parsec over the Lightyear. since the light year makes it so much easier to use c = 1 ly/yr. I guess its because when c =1, then the unit circle makes the wavelength of light an irrational number again? The precise value of pi is uncertain to me. Re:the second issue: I misspoke, and had addressed that mistake already. But again: While circles can be defined to have either a rational value for the circumference or radius, but not both, by defining a meter the way they did, it makes it so that measuring the circumference of circles that occur in nature when using metric always be a rational result.

The collatz conjecture If for any given positive integer n, a series is created such that: If the number is even, divide it by two. If the number is odd, triple it and add one. Then the Collatz Conjecture states that if the operation repeats often enough, the resulting series of integers created will always converge to 1 regardless of the size of n. Proof: If you tripple any odd number and add one the result will always be an even number. If you divide any even number by two, then half of the results will be odd while the other half will be even. Since every odd number will be changed to an even number by 3n+1 then we know a divide by 2 will always follow. ⇒ for any odd number we can instead apply: (3n+1)/2, i.e. half of the results for all operations will be odd and the other half will be even. ⇒ half of the time the number will expand to slightly more than 3n/2, while the other half of the time, the number will contract to n/2. ⇒ 3n/2·n/2 = 3n/4 or for the long term average the number will be reduced by 25%.per operation on the series. For any given positive integer, n, such that all integers < n have already been proven to converge to 1, then any series that drops below n will then converge to one. Since the long term average is -EV to about 3n/4, then all series must drop below n eventually.

Thanks, it seems like the math formatting didnt take at least on my browser making it difficult for me to distinguish symbolism from syntax. I can just google the identity/series to read them so its not a big deal. I just thought Id mention it to double check that it wasnt a compatiblility problem with my browser. (safari on iPad) that had always lacked the math syntax feature for writing math, though it always read the syntax fine in the old forum format. much bettr, thanks. edit to add: How diid you get the quoteed portion in my reply to update? Is that a new forum option that I’m not aware of? so is the point of that result being that pi is constructed from a series of rational fractions which is an irrational result due to the series being infinite? Curiouser and curiouser, now the two quotes are showing series that are the inverse opposites of each other lol.

I edited my reply to pzkpfw. when I missed the point he was making. I was confused by his rounding the value of the example I gave and missed his point that defining a circle would only change the radius to be irrational. I acknowledged my mistake and made a counter point but a couple of corss-posts didnt see it and replied based on my origional error. I’m reposting to clarify where our thinking is currently at so as not to create future confusion.

I think you may have misread the post. ie, by defining the metric unit to a circumference of a circle it causes all circumferences expressed in metric units to be a rational number. I could be wrong about that as I didnt have a chance to check my work. but this is something that I seem to recall as being understood, so I would prefer to search for a corresponding explanation. edit to add: I think I misunderstood what you were suggesting in that we could define a circle to having a definitive circumference. That’s true but I don't know how useful that would be since we usually measure distances that lie on a circumference. Therefore we could always assume that measurements in metric would have some definitive value. I also think the value of any wavelength should have a definitive value at least in theory, even if there will always be some error in our measurements.

Connecting the definition of the meter to pi if taken from the origional definition is more direct an explanation, but defining the meter based on the speed of light accomplishes the same thing, I think. Ignoring the fact that the Earth is a flawed ecample of a circle. Lets assume for arguements sake that the Earth is a perfect sphere so It’s easier to explain. We know that the definition of the circumference of a circle is 2πr which for a unit circle is just 2π. We know that π is an irrational number. Therefore the circumference of a circle should always be an irational number, that is, unless we define a metric unit in terms of the circumference of a circle. For example: If we try to measure the verticle circumference of the Earth based on a yard which is defined based on some kings shoe-size or something to that effect, then we would expect the circumference to be: 43,744,531.934 yards with never ending decimal places due to being an irrational number tied to pi being an irrational number. Why this is inconvenient is the concept of harmonics which involve waves that are perfect whole multiples of 1/2λ of the fundamental wave which is tied to the circumference of a unit circle. But if the wavelength i.e. circumference of the unit circle was always an irrational number, then It requires finding a perfect whole multiple of an irrational number, wich you can never perfectly calculate. By defining a meter to be 1/10 millionth of the distance from equater to N Pole, then the circumference of the earth is an integer of 40 million meters. What’s more all circles regardless of their size can be expressed as a rational number when using the metric system, all because of how the meter is defined. Therefore we can always calculate the whole multiples of harmonics waves because the fundamental wave is always a rational number. By defining the speed of light as an integer in meters we actually accomplish the exact same thing. it just requires more steps to explain why. In essence we have taken the uncertainty of our measurements of circles and thransered it to be uncertainty of the length of a meter. But thats not a problem because we cannot create things any more accuratly then we can measure them. so the meter being uncertain is never an issue for us in the human domain I hope that makes sense, because I only just now worked out the details of that confusing but ingenious definition for the meter. Correction: A unit circle would still have an irational circumference because the radius is defined as 1 so the circumference must be 2π. However the concept still applies to any wavelength that has some length that is not based on a unit circle. I appologize if my getting that backwards cused some confusion.

I didn’t choose to not reply, I was just too focused on a long reply to Swansots post, so I missed it. I apologize. Regarding your first reply, your right, in that I should have said the “wavelength of a sine-wave is 2π” not the “length of a sine wave is 2π”. Although in terms of time or wave propagation distance wavelength is the correct application. Regarding the connection of pi to the definition of a meter, I covered it in the reply to swansot but it is a very confusing concept so I will take some extra time to try and clarify my reasoning before replying.

edit to add: Sorry to keep adding more, but I should say that I also expect uncertainty to be linked to irrational numbers. so in the case of a circumference (2πr) or a wavelength (2π) then the uncertainty of a meter is expressed as the uncertainty of π. For cartessian coordinates, uncertainty carries over via the uncertainty of square roots through pythagoreans theorem. It was an epiphany that hit me in the result of my solution for the millenium problem in the TSP problem.

1. You’re right about the values, thanks for correcting me. I also agree that using the Earth was an invalid example. It’s certainly not a perfect circle especially in the verticle plane since it buldges at the equator, which I assume is why it was changed to be defined based on c. Don’t get me wrong, I think it’s an ingenious way to put uncertainty in its proper place, since it is our perception of the nature of reality that is what we must be uncertain and not reality itself. For example, uncertainty of a meter should never have any impact on the human domain since nothing can be made to a greater accuracy than we can theoreticaly measure it. 2. I’m sorry to disagree, there are only 2 variables and 1 constant in defininging the speed of light through a vacuum, the value of c and the definition of either a meter or a second. Since it is the the meter that is being defined then it must be that c is the absolute number and the meter is the uncertain unit of measure. 3. The link is the relativistic effect of time dilation and length contraction due to the constancy of c also effects frequency (inverse time) and 1/2 wavelength as the smallest unit of length for a wave in an inverse manor. Since time and distance are always equivalent in terms of EM radiation or electronic signals that propagate at the speed of light (not to be confused with the relatively slow drift speed of electrons). Then c becomes the fixed datum for measuring frequency and wavelength that are absolute variables in a way. as frequency increases, then wavelength must decrease in an absolutely proportionate way: f = 1/λ So at the beginning of the paradigm shift in the late eighties, in high speed (in terms of frequency) digital design, I thought of the shift as an effect of frequency expansion and wavelength contraction, that we don’t think of as being strange because we always thought of the speed of light as being constant and distance and time being equivalent, at least in that field of study which is the application of electromagnetic field theory. However, if we think of it from a srinking waves point of view, then the world seems to be growing. There is much more to it than that but that is my general thinking. I also applied the conservation of information from quantum field theory in terms of Special Relativity. BTW, just because concepts may come from a different field of study, it doesn't mean they can’t be properly applied in other fields as long as its applied in a valid manor. Hawking applied it in terms of black holes which was what led to the concept of a firewall on the EH. I proposed it as a matter/antimatter annihilation at the EH which is the same thing but includes the causality for the released energy. BTW, apparantly someone else has made similar proposals as their is a new reference in Wikipedia for frequency in terms of wave guides including the Lorentz Factor. correction: I should have called it relativistic impedance of a wave in terms of frequency here’s a link. https://en.wikipedia.org/wiki/Wave_impedance?wprov=sfsi1 Edit to add: BTW, I forgot to mention that their was also what I initially thought must be a strange coincidence in that the paradigm shift seemed to begin having an impact at around 30 MHz or 30 million cycles/sec. The relativistic effect begins to be significant at about 0.1c or roughly 30 million m/s. So, like I said, I thought it had to be a coincidence because I thought the definition of a meter was arbitrary relative to light. But thats one hell of a coincidence because 30 million is a very large number. Then once I discovered a meter wasnt so arbitrary after all, I started to try and understand the concepts involved. The result implies a link to how a meter is defined and what we know about a cycle which could be thought of as a wavelength (or period). the one thing we know is the fact that a wave stops behaving like a wave at geometries smaller than 1/2 λ. and that harmonically speaking, they must always be in hole units of 1/2λ Also note that if you plot the inverse of the Lorentz factor vs speed from 0-c it is 1/4 of a circle.

When calculating the circumference of a circle, we use 2πr. Since π is an irrational number, then for a unit circle, for example, the circumference must be an irrational length. However, the meter was origionally based on being one billionth the distance between the N. Pole and the Equator thus making the circumference of the Earth an integer in terms of meters. The meter was later changed to be based on the speed of light to again force the value of c in a vacuum to be an integer in meters/second despite an uncertainty of 4 parts in a billion. i.e. the uncertainty then becomes the length of the meter. It is the relationship of the speed of light to the circumference of a circle and therefore the length of a sine-wave (2π) that I am interested in confirming my understanding is correct as I am trying to verify that there is a link between wavelength and relativistic effects. Thanks.

ok, thanks. It looks like I couldn’t find it before due to a bug the in the Sefari refresh. The bottom of the page that was displayed was this forum: “Other Sciences” and there was nothing displayed below that when I last looked.

What happened to the philosophy forum? I’m nearly certain that scienceforums.net included a philosophy forum at one point. Was it scrubbed due to lack of use? if so, I’m curious to know when was it scrubbed?

Why does it look like each city has 3 coordinates? You only need two coordinates for a 2D plane. Square roots shouldn’t be an issue for a problem that small. Excel handles calculations of distances in loops with 30 city’s, most involving irrational numbers, without any lag and Excel is not exactly known for it’s efficiency. Perhaps your calculating relative distances which end up as 0 due to being in a loop? You may want to check to make sure negative distances aren’t being included.

The answer is that length contraction is real but it depends on the point of view that determines how it's real and to whom it's real. Assume there is a ship traveling from Alpha Centauri to the Earth at 80% c. You will often hear it said that the moving frame will be length contracted. This is a confusing statement that can be misleading. From any inertial reference frame (non accelerating), the observer is considered to be in the stationary frame and the moving frame is the frame that is in motion relative to that observer. Therefore from the ships PoV, the ship is normal and it is the Earth's frame that is in motion and the Earth, the sun, the entire solar system and including the orbit of the planets that is length contracted by 60% But from the Earth's PoV, it is the ship's frame that is length contracted so the Earth is normal and the ship is 60% shorter. So is it real? Yes its real and has real consequences such as demonstrated in the Twin Paradox. ( BTW, not all effects are real, but time dilation and length contraction are both real.) So what is actually being contracted? It is the dimension of space in the direction of travel for the moving frame that is being contracted. Therefore everything in that dimension that is moving along within the frame is being contracted at the same time. Note that there is another interpretation of SR that length contraction is an effect of the rotation of spacetime into the complex plane, or a hidden dimension of spacetime that is at 90° phase shifted from our spacetime. It's just an explanation for what is causing the effects but is still consistent with all results. It makes a certain amount of sense though. i.e. if you view a yard stick from the side it appears to be 3 feet long. as you rotate it,, it appears to be length contracted. The difference being the rotation is into another dimension so the length contraction is real.

I see what your saying. You're essentially using geometric constructions for creating convex polygons as idealized cases for the arrangement of cities to create the shortest possible path. However as the problem is presented, the cities are arranged arbitrarily without the user actually being allowed to effect their arrangement for the purpose of creating a favorable outcome. The confusion may have come from my hypothetical description of idealized arrangements of cities always forming a regular complex polygon. The point was to demonstrate the kind goals that are indicative of examples that are more or less optimal. Note that the main metric is non-intuitive. I accidentally neglected to include it in my last response.. So here it is now: The loop that creates the shortest path between all cities is the loop that encompasses the greatest area. While this sounds non-intuitive, you should be able to see that regular convex polygons such as an octagon, are indeed encompasing the greatest area. Note that the perimeter path that encompases all cities is also a convex polygon, although probably irregular in shape. Never the less it is representative of the optimal path for that particular subset of cities connected by the path.. So if I add a city that is the nearest to the perimeter, it represents a newly created triangle that adds a concave (pointing in) angle to the polygon. (see second example in the OP) Of course adding cities to the path always makes the path longer, so we need to choose a triangle that adds the least amount of length to the path and it must be something that a computer can guage. That was the reason for giving the three metrics by which the optimal triangle option would be based. Its not always certain which metric will produce the optimal result, but it should be at least one of the three or possibly one of two cases. Those are the cases I need to study in detail perhaps finding the case where the optimal choice can always be found directly. Note: just as you said, using circles adds utility for creating metrics to make judgements from but using triangles does the same thing, perhaps more efficiently. It's similar to how a 2-D field solver works where shapes that need to be modeled are broken down into constituent triangles enableing calculations throughout the framework. It's a lot to take in but I hope this helps. Thanks for providing the code. Unfortunately I don't know c as I'm not a professional programmer (EE Engineer). So I'm not sure what's going on with what appears to be arrays with some kind ov properties attached. Also I don't have easy acess to a PC to run it on (very long story). Could you possibly include comment statements?

This is a simple hypothetical problem intended to illustrate a certain concept for a group of problems that seem easy to solve or verify in one direction only. So finding a valid solution to the problem in the opposite direction should provide the answer. This is not intended as some kind of trick question. What it says is all that we may assume to be true.

How is that inconsistent? A 2D plane can cover any distance.

Right, I agree, so if we start from a least efficient solution, it would be what we call a full game solution, in game theory or simply checking every possible permutation to find the shortest path which would be a factorial expansion or require n! steps Which is a very rapid expansion that exceeds polynomial time. Alternatively, if we could literally move the cities with some mimum distance to each other in ofrder to design the shortest path it would always require the cities to be located on equidistant points of a circle to form a symetrical polygon: e.g. for n = 3 it would be a triangle as opposed to three cities in a line. for n = 4 it would be a square as opposed to an hourglass path. for n = 5 it would be a Pentagon and so on... Next we define a perimeter path for the outermost cities that encompass all other cities to create a polygon, though it may be irregular, its still clearly the most efficient path for that particular subset of cities. Next we add each unconnected city starting with those closest to the perimeter and it would be clear that when adding most cities, they would have one clearly optimal solution. Already reducing n! dramatically. I will stop the proof short right here for now until I've worked it down to the most optimal method that I can prove for all cases of cities, before I formalize it. To that end, I have discovered all the methods required for making the proper calculations of dimensions, distance, angles and areas which will be implemented to automatically so that I can study potential options with each change. I'm hopeful that I will yield a single optimal option for every city which I believe would be called a non-deterministic solution in mathematical terminology. Yes, in a plane. I think the perimiter path or perimeter cities could be uniquely defined as all cities that form a path such that all, as yet, unconnected cities are encompased and all perimeter cities form an angle pointing out from the center, (Sorry, I cant recall the name used to describe that condition.) Thank you, I really appreciate the kind words. Due to the huge potential for commercial applications, and the fact that I need to monetize a project soon to continue to pay the rent, I'm afraid that I need to be a little more careful as to what I can show. I will try to provide any previously known portions of the solutions as I find that they are not original, but as I said before, I like to finish a project to some degree, before doing a search for originality. Thanks for your understanding.

I'm not sure I understand your question. This problem was given as the classic example for p=np by several sources, including the site that's awarding the prize. How it relates to polynomials, I assume has to do with the number of permutations for cities involved, but ask the site to get their official point of, view.

I'm still working on the process for making it a fully automated solution. Step 8 is a problem that makes the process a nested iterative solution, or so I would imagine. However, I have a feeling that it may be connected to the three criteria for identifying the optimal triangle. i.e. if all three criteria of shortest distance, greatest angle and smallest area could not be satisfied simultaniously, then it may be an indication of a local minima, but I need to verify that in Excell where its still transparent. (edit to add: I agree that it seems like local minimas seem to be an arbitrary condition as opposed to finding a direct connection, but there are examples of arbitrary being an illusion when loops are involved.) I've automated the calculations for length, area and angles of the triangles, however, calculating the closest distance seems like a Heisenberg type issue, where, if you equated the grid dimensions to a Plank size it would create an ambigious distance between the vertex of the obtuse angle and the hypotenuse when the hypotenuse was not at an orthogonal angle. Put another way, if you divided the grid to be smaller and smaller to it's infinitessimal limit, it would produce an irrational number for the distance. Though I'm hoping it would be a rational number. I need to think about that a little more. I could use someones help, for a cut of the prize money, with programming the solution and submitting the paper for publication since the prize money is attached to a published solution, effectively qualifying only those with a PHD in math or computer science as far as I know. I've heard it said that anyone could be published, but I always equated that with saying anyone with the right skills could be in the NBA (but probably not if you never played on a scouted team).