wtf

Yes ok, but who said there was one? The process 1, 2, 3, 4, ... is endless. Infinite if you like. It never ends. So we say that the quantity of natural numbers is infinite. Why does this trouble you? There is no "last" number right before infinity, there's just the endless sequence 1, 2, 3, ... Or in set theory, we can collect all of them into a set: {1, 2, 3, 4, ...}. What of it? Why is this troubling you? If it was pushed away to point 47, the distance would be 47. No matter where you push it away to, the distance is finite. If you conceptualize a "point at infinity," as is done in the extended real number system, then the distance is infinity. But again, what about this is troubling you?

We don't usually think of transfinite cardinals as measuring distance. They measure quantity. But even though I understand this point, I don't see the heart of your objection. Sure, in the extended real number system there is an infinite distance between 0 and the point at infinity. But this doesn't really mean anything in terms of what you 'are saying. And especially, going back to your original question, about the R(n)'s. Each set {1, 2, 3, ..., n} is a finite set, and there are infinitely many such sets. There is just no mystery there.

For sake of conversation, I'll put on my materialist hat and agree that there must be a naturalistic explanation of consciousness. Although in passing I mention that the naive view of materialism, that the world consists of particles flying around and banging into each other to form atoms and galaxies and elephants and parliaments, is contradicted by modern physics; which states that particles are nothing more than excitations in quantum fields; and that quantum fields are nothing more than probability waves, having no physical reality at all. Materialism's not what it used to be, if it ever was. But never mind all that. I'll stipulate that we live in a world of particles flying around banging into each other, and somehow we are conscious, and that any theory of consciousness must show how particles (which aren't really particles, according to physics) somehow instantiate consciousness in some, but not all, macroscopic things. Why humans and not rocks, for example? Why ChatGpt (or more sophisticated AI systems to come) and not elevators, a question (a good one, I thought) that I asked you and that you did not answer. Indeed. And this is the distinction that I make, that was the point of the elevator question. I agree (for sake of discussion) that consciousness is natural. But that is not the same as saying that consciousness is computational. At least one prominent deep thinker, Sir Roger Penrose, thinks that it is not. Computation is extremely limited. The first thing they teach you about computation in computer science class is that there exist naturally stated problems that can NOT, even in theory, be solved by any kind of physically implementable computation. (That is, I'm not considering oracle machines as part of computation). When you (or anyone) claims that a program implemented on standard computing hardware might somehow achieve consciousness, by means of "supervenience" or "emergence," -- two impressive-sounding words that in my opinion convey no meaning and explain nothing -- you (or they, if you didn't say this) are making the claim that consciousness is computable. There is no evidence that this is true. The "evidence" consists generally of equivocation of words. They'll say that "Minds process information, and computers process information, therefore minds are computers," without noticing that the processing in question is qualitatively different. You agree with me, I believe, since you did put flipping neurons in quote. I take that as implicit acknowledgement that you already agree with my point: that there is no evidence that consciousness is a computational phenomenon, even if we agree (for sake of discussion) that it is a natural one. Yes certainly. But neurons are NOT digital logic gates. They're decidedly different. Neurotransmitters in the synapses are highly analog processes, not digital. We are very far from a full understanding or even a partial understanding of how neural processing works; and we have NO theory at all as to how qualia, or subjective experiences, arise from the brain goo. It's not premature to speculate that consciousness goes far beyond the profound limitations of digital computing. Nor are such speculations premature, as the argument goes back to Searle's Chinese room argument from the 1980s. Such speculations are 40 years old now; hardly "premature." They're mature, if anything. Flipping bits encodes no meaning. The meaning is provided by the human beings who flip the bits. Ok. But if not ChatGpt, then perhaps some future computer program or AI system. But all these systems run on perfectly conventional hardware, no different than the chips in your laptop or smartphone on which you're reading this. If bit flipping can instantiate consciousness, then why isn't an elevator conscious? After all it "remembers" what buttons have been pressed, and it "decides" whether to stop on each floor. Remembering and deciding ... those are things that minds do. Elevators must have some sort of primitive minds. That would be the argument for AI consciousness. I don't find it compelling. I would ask you to respond directly to my question about the elevator. If a computer-based system could be conscious or have some concept of meaning, can an elevator? If not, why not? Why one collection of digital switches and not another? I didn't find the remark about the lottery numbers particularly enlightening. Nor do I find computer-based, digital AI systems remotely like new born babies. Their learning systems are completely different. Their interactions with the world are completely different. I reject this analogy totally. What a wonderful compliment, thank you! After all, the title of the thread is "How does ChatGpt work?" If I was able to shed some light on the topic at a nontechnical but essentially correct level, I'm happy. Hardly a withering criticism, since nobody else in the world has the slightest idea either. So what say you about the elevator? If a pile of digital logic gates in an AI implementation might be conscious, how about a smaller pile of logic gates in an elevator that remembers and decides? Is it only the size of the pile of logic gates? It can't just be the size, else large rocks would be smarter than small ones, and we don't think rocks are very smart. What makes a pile of digital switches conscious? What makes you think a pile of digital switches might be conscious, when in fact human cognition is so radically and qualitatively different than digital switching?

If you agree with what I wrote but don't seen how this solves your issue, then I do not understand your issue. How do you figure that? Name a meter of paint that can't be labeled with a normal finite-length natural number. Likewise, name a point on the real number line that can't be labelled with a finite real number. What kind of line are you imagining that isn't the real number line?

No mistake, this is exactly the point you seem to be having trouble with. What is infinitely far? I challenge you to give me any two numbers that are "infinitely far" apart. On the contrary, if you pick any two real numbers, the distance between them is always finite. Can you see that? Try some examples. 10 and 47. Distance is 37. Try the distance between 0 and googolplex. Distance is googolplex, a finite number. Can you see that even though the real number line is infinitely long, the distance between any two points on it is finite? It's imperative that you see this. Try some examples for yourself. You cannot find any two numbers that are "infinitely far" from one another. Can you see this?

There is no paint infinitely far away. Pick any point on the line of paint. It's a finite distance from where you started. It's true that the line of paint is infinitely long. But there is no point on the line that is infinitely far away from anything else on the line. Let the line of paint be modeled by the usual real number line. I challenge you to identify any two points on the line that are an "infinite distance" from each other. On the contrary, if any two points on the line are labeled x and y, then their distance is the finite real number |x - y|. Can you see that? There is never an "infinite distance" between any two points on the real number line.

Can you explain clearly what you mean by that? Does the meaning of stopping on a particular floor supervene on an elevator when you press the button for that floor? Clearly you don't believe that, since you put 'flipping' in quotes. The quotes, I assume, indicate that you understand that biological neurons are nothing at all like bits in a digital computer. So what exactly do you mean? Please be clear so that I can understand your meaning.

To the best of my understanding of this thread, the heart of your issue seems to be that you don't quite get the following idea: Each of the individual natural numbers 0, 1, 2, 3, 4, 5, ... is itself a finite quantity. And there are infinitely many of them. In other words there are infinitely many finite things. And for some reason you have trouble going back and forth between those two levels. The finitude of each of the natural numbers, and the endlessness, or infinitude, of the procession of all of them via the process of endlessly adding 1. There are infinitely many natural numbers, and each of them are finite. Likewise each R(n) = {1, 2, 3, ..., n} is a finite set; and there are infinitely many of the finite sets R(n), namely R(1), R(2), R(3), etc. Hope this is helpful.

How it works is pretty simple, and once you understand how it works it's not frightening and it's not going to replace us. It's no smarter than an elevator that knows what floor to stop on based on what button you pushed. They take a huge body of text, everything they can get their hands on. In fact the sources of this data are interesting and of course represent choices made by the programmers. In other words ChatGpt is built by humans and encodes the biases of the humans who built it. Here's their own description of the data. https://www.stylefactoryproductions.com/blog/chatgpt-statistics So they start out basically with a lot of digitized books, and a lot of web pages and Reddit answers. Nothing that isn't already digitized, and skewed toward Reddit users. Ok. Then they apply incredibly sophisticated statistical analysis to make up rules on the fly such as "When you see this phrase, 86% of the time you see this other phrase." They take that basic idea to its most sophisticated level, where ChatGpt can even pass law exams and explain physics to people. That's impressive statistical pattern matching. But at heart it is just a big adding machine, crunching text it doesn't understand, and figuring out what strings of symbols are typically followed by what other strings of symbols. It has no meaning. The meaning is in the minds of we humans. That's the difference. It flips bits. We experience meaning. It does not "understand" anything. It doesn't know anything. It doesn't feel anything. It just reads in some data and calculates the correlations among the data. It's so mechanical that you could program a computer to do it. And that's literally what they do. It's not a human being. It's a smart elevator. The real danger is the foolish humans who think it's some kind of god. Humanity's next graven image. Something to worship, something to fear, something to exploit. That's all, no more and no less than any of humanity's other clever tricks like fire and the wheel and the printing press and the Internet and civilization itself. ChatGpt-like systems are profound but not existential. We'll be fine.

No reason Katy couldn't have adopted someone older than herself. Score one for the bot. Ok so I looked this up. (I'm a good bot myself). In 43 states you can adopt someone older than you. In the other 7, you must be from 10-15 years older than the person you adopt. https://www.thehivelaw.com/blog/can-you-adopt-someone-older-than-you/

It's the Euclidean algorithm. Study this page and work out some examples by hand to see how it works. https://en.wikipedia.org/wiki/Euclidean_algorithm Actually the Wiki page is a little confusing, here's a simpler one I found. https://sites.math.rutgers.edu/~greenfie/gs2004/euclid.html

This is the opposite of the way you originally expressed it, and this implication is false as well. Suppose X and Y have different truth values. Then X xor Y is true; and X xnor Y is false. True implies False is a false material implication. Your claim is false in both directions.

But the implication is manifestly false, as I noted. If X and Y have the same truth value, then their xnor is true and their xor is false, resulting in a false material implication. Agree or disagree? Didn't understand this. Sets of knowledge? What do you mean? 1901 old? The Pythagorean theorem is from 500BC and was known even before that.

The xnor logical connective is true if and only if X and Y have the same truth values. xor is true if and only if X and Y have different truth values. So far so good. What does -> mean in this context? Is this a logical implication? That seems unlikely, since if X and Y have the same truth values, X xnor Y is true and X xor Y is false, resulting in a false material implication. So, what do you mean by -> here? Mathematical functions never create news sets. Given two sets, there may be functions between them. But the sets have to already exist. Functions do relate them in terms of inputs and outputs, but this isn't a very meaningful way to put it. The symmetric difference of two sets is the set of elements that are members of one of the sets but not the other. A web search on symmetric addition did not bring up any definition at all. What is symmetric addition. What is symmetric addition? And as before, what does -> mean? By relationship, do you mean relation? A relation between two sets X and Y is a subset of the Cartesian product of X and Y. That is, given two sets X and Y, a relation between them is a collection of pairs (x,y) that satisfy the relation. Is that what you mean by relationship? If not, what do you mean by relationship? What is a similarity between two sets? Given two sets X and Y, how do I know if they are similar or not? What definition are you using? Secondly, Russell showed in 1901 that there is no universal set. Are you working with some restricted universe of sets? Can you clarify what you mean by universal set? What is potentially a fractal, and how so? I believe you may have had some interesting personal insight about sets, but your exposition is unclear. I hope my questions can help you to better explain what you are saying.

A point in the Cartesian plane is characterized by an ordered pair of real numbers. But just as with the line, this is misleading. In math there is no geometrical plane. Rather, there are the real numbers, and then ordered pairs of real numbers. And we call the set of ordered pairs of real numbers the "plane" as a geometrical visualization. But there aren't two things, the plane and the set of ordered pairs. There's only one thing, the set of ordered pairs, which we commonly refer to as "the plane," or, when equipped with the Euclidean metric, the Euclidean plane. But it's still just the set of ordered pairs of real numbers. The geometry is just a convenient visualization and way of speaking. To emphasize this point, what else can we do with ordered pairs of real numbers? We can define a "funny multiplication" on them, and then they turn into, voilà, the complex numbers C . So would we say that the Euclidean plane and the complex numbers are "the same?" Or would we say, rather, that the Euclidean plane and the complex numbers are two different interpretations of the same underlying set of ordered pairs of reals? I'm mentioning all this because you are insistent in wanting to know how the pairs of real numbers "describe" or "map to" the plane. But in fact, there is no plane. There's only the set of ordered pairs of real numbers, which, as you note, is called \( \mathbb R^2 \). This is all a bit philosophical or semantic and I don't want to make too much of it. But you may be asking the wrong question. The set of ordered pairs IS the plane, it doesn't map to relate to the plane. If that helps. Yes you get 0 as the limit. To be clear, in the example of 1/2, 3/4, 7/8, ... we get 1 as the limit. I assume that's what you meant. So how does this work? Let's take the example of the sequence 1/2, 1/3, 1/4, 1/5, 1/6, ... The sequence has 0 as its limit. That means that the terms of the sequence get, and stay, arbitrarily close to 0. That's formalized as the "epsilon" business that people see briefly, in passing, in a beginning calculus course, before getting on to the calculational aspects. Note that every element of that sequence is NOT zero. This is crucial to the limit concept. The elements of the sequence never "become" zero. Zero is not an element of the sequence. Rather, the sequence has the limit of 0, where we take some pains to formally define what we mean by a limit. I did not read all the posts in this thread before arriving a few pages in. If you formerly held different beliefs, that might be generating some confusion. But even since you and I have been talking, you seem to believe that there is a largest element of [0,1), and that amounts to the same thing. So I cannot square this latest statement with what I've been talking to you about. The halving process refers (in our ongoing example of [0, 1)) to the sequence 1/2, 3/4, 7/8, 15/16, ... We can definitely do this infinitely many times, since that is an infinite sequence of rational numbers. There's an element (2^n - 1)/2^n for every natural number n. The limit of the sequence is 1. But where is the confusion? We have infinitely many terms, each of them finite, and they have a finite limit. No mystery at all. Nobody understands limiting processes in their first calculus course. There's a math major course called Real Analysis in which they nail all this stuff down tight as a drum. But very few people ever take that course. So a lot of people, especially technical people like engineers and physicists, are great at calculus but were never exposed to the subtleties of the nature of the real numbers and limiting processes. Perfectly normal. As a limit. I hope you see the ongoing theme of this post! In the Riemann integral, we take finer and finer partitions. Say the partitions have successive widths 1/2, 1/3, 1/4, 1/5, ... Every partition has nonzero width. The limit of the widths is zero. And in fact we do NOT require a "zero width" when defining the Riemann integral. Rather, for each partition, we calculate the corresponding Riemann sum, the sum of the areas of the finitely many rectangles in that partition; and we define the integral as the limit of the sequence of Riemann sums. As you can see, everything depends on a proper understanding of the limit concept. That's a little word-salady to me. What we were discussing above is whether there's a largest number in [0,1), which it turns out there isn't. So whatever interest you about the Riemann integral may have been explained before I joined the thread. Feel free to catch me up. And what is the "one dimensional aspect of the integral?" I don't know what you mean. I thought I explained it. You are correct that [0,1] and [1,2] have a point in common, and if you tried to rotate them past each other they'd indeed collide at the point 1. You are wondering how they can collide if the point 1 has zero length. I tried to analogize this with a Newtonian point mass. I said that even though 1 has zero length, zero dimension, zero volume, it can "still pack a punch." Did this analogy not resonate with you, even a little? Maybe it's kind of strained, I did admit that up front. But in your rotating visualization, the line segments will indeed collide at the point 1, simply because 1 is an element of each segment.

Yes, a real number represents a point, or the location or "address" of a point if you prefer, on a line. But in fact this is actually a circular definition, since in math "the real line" is just another name for the set of real numbers. There's not a separate thing called a line that happens to be indexed by real numbers. Rather, we construct the real numbers, and casually talk of "the real line" meaning exactly the set of real numbers. So there's a bit less here than meets the eye. Now when you say space, I hope you do not mean physical space as in physics; because the mathematical real numbers are very different (as far as we know) from anything in the physical world. In physics we have the Planck length, which is a length below which our equations of physics are not applicable. That doesn't mean that physical space has a smallest distance. Rather, it just means that below the Planck length we can't reason sensibly about the nature of space. But either way, math \( \neq \) physics, and that's always good to keep in mind. We are talking only about mathematical space and nothing to do with the world we live in. Unless you're talking about physics, in which case that's a whole different kettle of fish, as they say. 1/2, 3/4, 7/8, 15/16 ... Are there not infinitely many elements in that sequence? Isn't the halving process being carried out infinitely many times? I hope we can reach agreement on this point. There are infinitely many counting numbers 1, 2, 3, 4, ..., right? And for each counting number \( n \), we have an element of the sequence \(\frac{2^n - 1}{2^n}\). Right? Let's please nail this down. We are going "half the distance" an infinite number of times. Let me know if that's not clear because you seem to be disagreeing. Now I'm confused, because I thought you've been saying there is a largest number in [0,1), which amounts to saying that there is a smallest positive real number. If you don't believe this, and if you claim you have never believed this, then I wonder what we've been talking about. You've been claiming there's a smallest positive real number in multiple posts. Am I completely misunderstanding you? Sorry these two quotes are out of order but it seems to be ok. No, the number of partitions is NEVER infinity. The number of partitions is always some finite natural number \( n \). As \( n \) gets large, the upper and lower Riemann sums may happen to approach the same number as a limit; and if they do, we call that number the (definite) Riemann integral. Maybe the wording's a little confusing. As we let \( n \) go to infinity, for each \( n \) we have a pair of numbers, the upper and lower Riemann sums; so we get two infinite sequences. If each sequence has a limit and the two limits are the same, we call that limit the Riemann integral. But there are never "infinitely many" partitions. That's an informal way of talking about the limit. The entire idea of calculus is to use limiting processes to avoid talking about "infinitely many" partitions or "infinitely small" things. We are not filling the space, we're approximating it with rectangles, and the limit of the approximation process is the area under the curve. It's a limiting process. I'm not entirely sure what you mean that studying the Riemann integral will help you figure this out. You've been concerned with the question of finding a "last" number in [0,1), and you seem to agree that we have proved that there can be no such thing. Is there a different concern you have about something else? Integration can't help. If (in two dimensions, say) we include or don't include the boundary of a disk, the area is still the same. That's the point we made earlier, that the lengths of [0,1] and [0,1) are exactly the same, namely 1. Points have no length or area, so their presence or absence makes no difference to an integral.

To strain an analogy, when you buy a dozen eggs, there are 12 eggs in the carton. But when you open up the carton you do not find the number 12. You find 12 eggs. Likewise there are uncountably many real numbers, \( 2^{\aleph_0} \) in fact, in the interval [0,1], or in any other interval of the reals. But you will not find \( 2^{\aleph_0} \) among the real numbers. Hope this is clear. You've asked this several times, and each time you get the same answer. If you start from x = 1/2, repeating the halving process gives an infinite sequence of real numbers 1/2, 3/4, 7/89, 15/16/ 31/32, etc. None of them are the largest number in [0,1). In fact this example provides a nice intuition for the fact that in [0,1), the point at 1 is a limit point of the set. There is an infinite sequence of points getting closer and closer to 1, but there is no last point in the sequence. If it helps visualization, think of it the other way. Start with 1 and keep halving: 1, 1/2, 1/4, 1/8, 1/16, ... There are infinitely many numbers in the sequence. There is no "last" number. This shows in fact that there is no smallest positive real number, just an infinite sequence of smaller and smaller positive reals that approach 0 as a limit. Ok, good. Does any of this help your intuition? One purpose in studying the formal properties of the real numbers is to improve our intuitions about them. You mean it's counterintuitive, and that's normal. Many people have an intuition that there's a smallest positive real, until they are shown the proof that there isn't. But in terms of logic, it's logic that shows that there can be no smallest positive real. That's because the real numbers are a field. In a field we can add, subtract, multiply, and divide (except by 0) any two numbers. So if someone claims that, say, \( x \) is the smallest positive real number, it's immediately clear that this is false; because \( \frac{x}{2} \) is also a positive real and it's strictly smaller than \( x \). You can see that, can't you? In terms of logic, we know that there can not possibly be a smallest positive real. Another example is the sequence .1, .01, .001, .0001, etc. The sequence goes on without end. There is no smallest real number. On the contrary. The hyperreals are also a field. They are an alternative model of the exact same first-order axioms that the reals are a model of. So if you claim that x is the smallest positive hyperreal, then x/2 is a smaller positive hyperreal. There is no smallest number, not even an infinitesimal, in the hyperreals. You can always divide a hyperreal infinitesimal by 2.

Thanks all. Must have been just one of those things.

In my recent post on the "Geometry of the real number line" thread here, https://www.scienceforums.net/topic/128915-concerns-about-the-geometry-of-the-real-number-line/page/4/#comment-1233011 I wrote the markup for (1 - x)/2 as \frac{1-x}{2} It rendered correctly when I committed the post. A few minutes later as I was checking for typos, I noticed that it had rendered as "1 - x2". So I edited my post, deleted the apparently faulty markup, and re-entered the correct markup. It looked fine when I committed my post. This morning as I was checking my mentions, I noticed that it had reverted to "1 - x2" again. Is this a known issue with the \frac command? Why did the markup render correctly for a while then revert to being rendered incorrectly?

Because the transfinite ordinals and cardinals are not real numbers. The subject of the thread is "The geometry of the real number line." That's YOUR topic, right? So we are discussing the real numbers. The transfinite ordinals and cardinals are fascinating in their own right, but have nothing to do with the real numbers. In fact the transfinite ordinals (and the cardinals, which are technically a proper subclass of the ordinals) do not intersect the real numbers at all. The transfinite ordinals and cardinals are neither subclasses nor superclasses of the real numbers. They're just a completely different subject. If you are trying to understand whether there's a largest number in [0,1), it's no help to think about transfinite numbers, since transfinite numbers are not in that interval at all. Does that make sense? Besides, haven't you already said you are only interested in the standard real numbers? Why are you suddenly interested in mathematical objects that are NOT standard real numbers? This para does not make sense. First, we can't use transfinite numbers in a discussion of the reals, because transfinite numbers are not members of the real numbers. We can of course use transfinite numbers to talk about the cardinality of various subsets of the reals, but that's not what we're talking about here. Ah. Well, the length of a single point is zero. The length of [0,1] is 1, and so is the length of [0,1). The addition or deletion of a single point makes no difference when we're calculating the length of an interval. I'll keep my clothes on if it's all the same to you, thanks. The length of a point is zero, so adding or deleting a point can not make any difference in the length of a line segment. I think what you are saying is that the intervals [0,5] and [5,6] both contain the number 5, and that is correct. I don't see how that helps you to find a largest number in [0,1). So the two intervals would "bang into each other" at the point 5. You are correct that 5 is an element of both intervals. But as a point, the number 5 has length 0. The two facts are both true. 5 is a point on the real number line and it has length 0. So yes, two points of zero length can still bang into each other, if you want to put it that way. Remember, Newton showed that you can reduce gravitational calculations to "point masses." So if it helps, you can think of them that way. They are points with zero dimensions, zero length, and zero volume, but they still pack a punch. I'm not saying that's any kind of mathematical argument, but if it helps you to resolve this particular objection, I'm ok with it. In your imagination. But the proof that there is no largest number in [0,1) should cause you to realize that your intuition is flawed. It should give you a better intuition. Now there is nothing wrong with having such a faulty intuition. Pretty much everyone has faulty intuitions about the real numbers before they see these technical discussions. But now that you've seen a formal proof that there is no largest number in [0,1), you should be willing to realize that your intuition is faulty, pre-mathematical as it were, and you should update your intuition. What exactly about the proof are you still unconvinced about? I asked you that in my previous post. It's no good for you to say you're unconvinced, without saying exactly what aspect of the proof you are unsure about. If you could focus on the proof we could discuss that. I can't discuss onions or bodies of water or vague pre-mathematical notions of the real numbers. It's more helpful to focus on the actual math. We are not going to discover a largest number in [0,1), because we already proved a few posts back that there is no such thing. Now I'm confused. Didn't you see and more or less agree with the proof I already posted? There is no largest number in [0,1). Proof: Suppose you claim that x∈[0,1) is the largest number in that set. Take half the distance between x and 1 , namely 1−x2 and add it to x , giving: x+1−x2 You can see that we have the strict inequality x<x+1−x2<1 so that x is not the largest number in [0,1) after all. Since x is entirely arbitrary, we have just shown that there is no largest number in [0,1). You have already seen this proof, and more or less said you agree with it. But now you are saying "Are you sure there are proofs?" You already saw the proof. Yes, I'm sure there's a proof, I've now stated it twice. And you've agreed to it. So I have no idea what you mean by asking if I'm sure there's a proof. Ah ... ps ... you said, am I sure THEY are proofs. Are you asking if the proof I gave is actually a proof? Yes, I'm sure. If there is any part of it you are unsure of, I wish you would ask about it or say which part you find unconvincing, so that we can focus on that.

This was in response to your question about what happens if we continually halve the distance to the end of [0, 1). But if you accept that, why are you still confused about halving the distance between p and q? In set theory, the continuum is just another name for the set of real numbers. In topology, a continuum is "a nonempty compact connected metric space." Either way, it's not entirely helpful to try to reason from the everyday or philosophical meaning of the word. https://en.wikipedia.org/wiki/Continuum_(topology) By the way, the set of real numbers is not compact. So according to Wikipedia, the real numbers are not a continuum. That's contrary to pretty much everybody. You have to take Wikipedia with a large grain of sodium chloride. In some ways yes, in some ways no. In terms of cardinality, they are exactly the same. In terms of length, they are exactly the same. In terms of topology, [0,1] is a compact set, which has many important properties that [0,1) lacks. For example any continuous function on a compact set must necessarily attain its maximum and minimum. This is not true of [0,1). So when you remove the end point some things don't change and other things do. Topologically, removing that one endpoint makes a huge difference. https://en.wikipedia.org/wiki/Compact_space Is this a physical onion, or an imaginary onion in your mind? If it's a physical onion, it does not have infinitely many layers. If it's imaginary, I don't know what you're imagining. But explain me this. Did you understand my earlier demonstration that no matter what number you claim is the largest in [0,1), it turns out that it is NOT the largest. Did you understand that? If so, why are you still tossing out imaginary onions? And if not, which part is unclear or unconvincing? One perfectly sensible response on your part would be, "Oh, I see. There can not logically be any largest element of [0,1). I shall adjust my intuitions accordingly." That's the purpose of the exercise, to sharpen and correct our intuitions. Not to talk about hypothetical imaginary onions after you've been shown a proof. If you dispute the proof, let's focus on that. Having seen the proof, why are you still insisting on an intuition that is falsified by the proof? Let's nail down the understanding of the proof that there is no largest number in [0,1). Once we do that, then it will be clear that all intuitions to the contrary are inaccurate. What he meant is that in higher set theory, we can study transfinite numbers, like the transfinite cardinals [math]\aleph_0, \aleph_1[/math], etc., and the transfinite ordinals ω,ω+1, , and so forth. These are far outside of the scope of our discussion, but that's what your professor was referring to. That was @Genady's comment on page one of this thread, credit where due. But if you understand that we can continually split the difference 1/2, 3/4, 7/8, etc., why are you still unclear about this? It's the same idea. Well FWIW nonstandard analysis is also a part of ZFC. But we are talking about the standard reals and need not go any further than that.

Say we start at x = 1/2. Then repeating the "half the distance" idea gives 3/4, 7/8, 15/16, 31/32, ... We get an infinite sequence of points, each one a little closer to 1, but none of them is the largest in [0,1). This is vague. Numbers aren't "attached to" each other as if by velcro for example. Didn't the two-dimensional example of the boundary of a circle help? Sometimes geometric intuition is helpful. Sometimes it's confusing. What is the formal definition of [0,1)? It's [math]\{x \in \mathbb R : 0 \leq x < 1\}[/math] That denotes the set of all real numbers greater than or equal to 0, and strictly less than 1. There's no "attachment" in the math. Just a set of real numbers. By the way this is set theory notation, since you mentioned Zermelo-Fraenkel. The curly brackets denote a set. The colon is read, "such that." The boldface [math]\mathbb R[/math] stands for the real numbers. So the notation literally denotes "The set of all real numbers x such that" etc. This analogy doesn't work for me. For one thing, water isn't the real numbers. Water is made of discrete molecules and exists in the physical world; while the real numbers are a mathematical abstraction that, as you note, form a continuum. But even on its own terms, the water analogy doesn't work. If you zoom in to the "surface" of a body of water, you find a cloud of molecules that aren't part of the body of water, but are in the process of evaporating into the air. In fact the surface of a body of water very nicely models an open set with no boundary at all. The surface is fuzzy, with molecules constantly jumping around and some of them escaping into the surrounding air. I don't understand it either, as shown by my example of zooming in to the "surface" to see a cloud of molecules leaving the water and evaporating into the air. There is no well-defined surface of a body of water. Now perhaps you are thinking of surface tension, but still, the analogy is strained. If you zoom in, you see molecules bouncing around. You can never point to any one collection of molecules and say, "That's the surface." Before you're done speaking, some of those molecules have evaporated into the air.

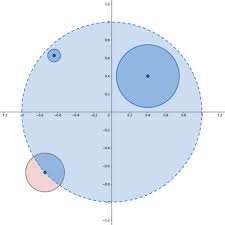
Thank you, glad it was helpful. After I wrote my post I went back and read through this entire thread, and I see I haven't actually said anything that hasn't already been said, so credit to all the others here before me. It's much more than that. It's a definitive proof that [math][0,1)[/math] has no largest element. Because if you claim that [math]x[/math] is the largest element, I can just note that [math]x + \frac{1 - x}{2}[/math] is strictly between [math]x[/math] and [math]1[/math]. I hope you can see that. This point was made by @Genady on page 1 of this thread. He noted that if p and q are real numbers then (p + q)/2 is a real number strictly between them. It's essentially the same argument that I just gave. Well it IS strange and interesting, that's why you asked! It is counterintuitive that given a real number, there is not a "next" point; and that if a line segment is missing its right endpoint, then it can't contain a largest number. Many people are confused about this, and it takes some understanding of the real numbers to correct our false intuitions. If it helps, think of the real numbers as maple syrup, or an infinitely stretchy rubber band; and not as a string of bowling balls. The real numbers are not lined up next to each other. Between any two real numbers are infinitely many more. Indeed, I just showed you a proof. Any candidate real number in [0, 1) that you might claim is the largest isn't. That's because you can take half the distance between your number and 1, and add it to x, to get a number strictly between your number and 1. It's a boundary point. That's one of the topological notions mentioned by @studiot on page 1. A boundary point has the property that any interval surrounding it necessarily contains points in the original interval, as well as points outside it. If you look at the closed unit interval [0,1] (remember that contains both endpoints) the right endpoint is indeed special. Any interval that contains it, such as, say, (.99, 1.01), contains points that are in [0,1] and also points not in [0,1]. That's the definition of a boundary point. A point in inside the interval, like 0.5, does not have that property. There are small intervals around 0.5 that are entirely contained within [0,1]. The name for that kind of point is interior point. So yes, boundary points are special. When you remove one of the endpoints from an interval, that end of the interval becomes open, and gets "fuzzy" if you think of it that way. It's sometimes more geometrically enlightening to think of it in two dimensions. Consider the unit disk consisting of all the points within 1 unit of the origin. If we include the boundary, we have the set [math]\{(x,y) : x^2 + y^2 \leq 1\}[/math]; and if we exclude the boundary, we have [math]\{(x,y) : x^2 + y^2 < 1\}[/math]. You can see that if we omit the boundary, for any point inside the disk, there's another point strictly between that point and the boundary. If we omit the boundary of the disk, there are no points that are "closest to the boundary." It gets fuzzy out there. Here's a picture I found online. You can see that a point on the boundary is characterized by the fact that any (blue and pink) disk we draw around it contains points of the original disk and points outside the disk. And any interior point is characterized by our ability to find a (blue) disk containing that point that's entirely within the original disk.

Consider this example. Consider the closed unit interval [math][0,1][/math] consisting of all the real numbers between 0 and 1, inclusive. Suppose that we delete 1 from the right-hand end, leaving us with [math][0,1) = \{x \in \mathbb R : 0 \leq x < 1\}[/math]. That is, we are considering the set of all real numbers greater than or equal to 1, and strictly less than 1. Now I claim that this set has no largest number, or no right-handed endpoint. How do I know that? Well, suppose you claim that, say, 3/4 is the largest. I'd just note that 7/8 is strictly larger and still strictly smaller than 1. And what if you say ok then how about 7/8? I'd note that 15/16 is strictly between 7/8 and 1. You can see that no matter what number you claim is the new right-hand endpoint, it can't be; because there is always a number halfway between your number and 1 that is strictly greater than your number, and strictly less than 1. Do you see that the interval [math][0,1)[/math] has no right-hand endpoint? If I have any set [math]X[/math] I can partition it into a collection of singletons as [math]\displaystyle X = \bigcup_{x \in X} \{x\}[/math] I've partitioned an arbitrary set such that "every partition contains exactly one member of the set and there are no empty partitions." That's not a Dedekind cut, it's just the trivial partitioning of a set into the union of its singletons. A Dedekind cut consists of a two-set partition of the rationals such that all the elements of one element of the partition are strictly less than all the elements of the other. For example defining sqrt(2) as the partition of the rationals into all the rationals whose squares are respectively less than 2 and greater than 2. Dedekind cuts are not particularly helpful to resolving the OP's concern about "next" real numbers; but I haven't read the entire thread so perhaps they're relevant to some other aspect.

My understanding is that these are just abstract mathematical functions. If you are in state X and an instruction puts you into state Y, that's a function, called the state transition function. They're not polynomials or exponentials or any familiar type of function. They're functions in the formal sense. Input state in, output state out. In https://en.wikipedia.org/wiki/Finite-state_machine, see the section marked Mathematical Model.