Widdekind

http://en.wikipedia.org/wiki/Weak_hypercharge the Weak-hyper-charge, of right-handed Fermions, is one-charge-unit larger (in magnitude), than their regular left-handed cousins... looking at the table provided on the page, the only way of conserving hyper-charge, as well as charge & spin, in transitions, from L <----> R... is to emit a spin-less pion = L-quark + R-antiquark (or vice versa)... only L/R quark/antiquark pairs, have no spin, and no charge, but a unit of hyper-charge, to carry away the unit of hyper-charge "lost", when (say) some R-electrons ----> L-electron so, can electrons expel pions, in transitioning from R ----> L handedness ?? to conserve charge, hyper-charge, momentum, angular momentum... a right-propagating, right-handed electron, would have to recoil backwards, whilst preserving its spin... and emitting a neutral pion (of zero spin) in its original forward direction... and originally have had enormous energy, to account for the 140MeV rest-mass of the pion pion emission resembles gluon emission, and so seems to smack of E/W + S unification... can electrons actually emit gluons / pions, in the process of reversing R-to-L handedness ??

in intuiting, that positrons are "hyper-spin up", and negatrons are the same but "hyper-spin down"... so the extrapolation, of the PXP, would be, that whereas electrons can "stack" spatially, if they spin oppositely, so two electrons could stack, if they hyper-spin oppositely, i.e. you could observe matter co-occupying the same space "xyz+w", as its antimatter "inverse-twin" now, if Fermions are actually spin-1 Bosons, half of whose spin points hyper-spatially (Sw = +/- 1/2)... in practice, that difference is equivalent to "rest-mass" vs. "mass-less"... the PXP would, then, derive from the "hyper-spatially directed hyper-momentum (pw2)" and/or "hyper-spatially directed spin (Sw)"... particles whose wave-functions are not "sloshing hyper-out and hyper-in" can stack over each other... but hyper-momentum must impede & impair such stacking... you can have two electrons, in exactly the same states, nano-scopically near each other, through space "xyz", e.g. in metallic crystal lattices... perhaps you can have two "Bosons", in exactly the same states, atto-scopically near each other, through the hyper-spatial "w" thickness dimension ? To wit, when you say you see two photons "in the same space", in simplified notation, the one is at "xyz,w" and the other at "xyz,w+dw"... if so, then this hyper-space hypothesis would predict, that due to the limited thickness "dw" of the fabric of space-time, so the stack-ability of bosons spatially (but at varying hyper-spatial "heights" out-in) would also be limited... photon-photon scattering ? -------------------------------------------------------------------------------------------------------------------------------- perhaps the Weinberg angle, which makes the mass of Z0 > W+/-, reflects the hyper-angle, at which Z0 propagate, both "across" the hyper-thickness of space-time, and also through standard spatial dimensions... whereas W-bosons "bounce back and forth" solely through the thin "thickness" hyper-dimension... the extra momentum-energy of the Z0 would then be greater by [math]m_Z^2 = p_w^2 + p_{xyz}^2 > p_w^2 = m_W^2[/math] according to the Weinberg-Salam equation [math]\frac{m_W}{m_Z} = cos(\theta_W) = \frac{A}{H}[/math] whereas i would suggest, seemingly similarly [math] = \frac{p_w^2}{p_w^2 + p_{xyz}^2}[/math] which is certainly similar (maybe more of a cos2 type of term) ( i tried to talk about HS here ) wait wait wait electrons & even neutrinos have "hyper-charge", which i'm interpreting, as electric charge, coupling into-and-through the 'thickness" hyper-dimension... i'm interpreting Z0 bosons, as hyper-dimension-ally directed photons, emitted when "hyper-spatially-charged" Fermions start to stack, and blast each other at "point blank range", atto-meters = 100GeV so, hyper-spatial charging => Fermions blast each other at hyper-high energies, if ever the seek to stack... whereas Bosons do not carry "hyper-charge" (the emission/absorption of bosons never affects "hyper-charge")... so, through the "thickness" hyper-dimension, Bosons are as non-interacting, as neutrinos are, through the three standard spatial dimensions... so, perhaps the PXP is "enforced" by Weak-bosons, interpreted as regular normal photons, except propagating through the "thickness" hyper-dimension "w", which blast between hyper-charged Fermions, whenever the seek to start stacking, w/in the thin "thickness" of space-time "dw". Z0 = "in-out" directed but otherwise normal regular photons... the PXP is "enforced" and is the result of, the hyper-charges, of (all) Fermions... so, since "Bosons" are un-hyper-charged, they act like neutrinos, hyper-spatially, so "stacking" as easily, as nearly-non-interacting neutrinos standard spatially "hyper-charge" defines the "B" quantum field, orthogonal to the W3 field... that starts to sound similar, to these simplistic suggestions... the "B0" eigenstate would be a perfectly-hyper-propagating photon... orthogonal to purely-space-propagating photons... the Z0 is a mixture of both, propagating mostly "in-out across" the fabric of space-time, but also propagating spatially to some extent... http://en.wikipedia.org/wiki/Weak_hypercharge

in a metal, the many many electrons' wave-functions overlap, at least when you take their modulus-squared = (charge) density distribution... so, why don't such electrons repel, according to PXP ? seemingly, if you propelled pairs of electrons at each other, then their wave functions would slam into each other, and of necessity overlap, at least for some mere moments in their interaction... would PXP apply ? or, is the PXP appropriate, to constant-energy stationary states, which are themselves "orthogonal", i.e. [math]\int d^3x \Psi^*_1(x)\Psi_2(x) = 0[/math] ? And, does that say, that (simplistically), the electrons' wave-functions never actually overlap, because at any given instant of time, the "orthogonality" of the wave-functions implies, that "whilst one electron is 'here', the other is 'there'", so that, instant by instant, the electrons are never actually co-occupying the exact same (set of) space-time event / points ? When you "smear over time", and take the squared modulus, you observe, that the electrons do "cycle through (some of) the same regions", i.e. their densities do overlap... but instant by instant, the actual probability amplitudes are "in different places" moment by moment ?

magnetic moment is, ultimately, purely magnetic fields... and EM fields can possess "mechanical" spin angular momentum... perhaps "swirling vector potential" could account, for said spin and also imply a magnetic moment (??)

[math]2 m_{\nu}c^2[math] could conceivably occur in Quasar spectra (??)

[math]\frac{r B'}{B} = A \left( \epsilon x^2 + 1 \right) - 1[/math] [math]\approx \frac{ \epsilon x^2 + 1 }{1 - \frac{1}{3} x^2 } - 1[/math] making the simplifying assumption of Schwarzschild (seemingly) [math]= \frac{ \left(\epsilon + \frac{1}{3}\right) x^2 }{1 - \frac{1}{3}x^2}[/math] [math]\longrightarrow[/math] (if P = constant) [math]B(x) = \left( \frac{1-\frac{R_S}{R}}{1-\frac{R_S}{R}\left(\frac{r}{R}\right)^2} \right)^{\frac{1+3 \epsilon}{2}}[/math][math]\times \left( 1 - \frac{R_S}{R} \right)[/math] [math] B + r B' = \left( \frac{8 \pi G P}{c^4} \right) \left( r^2 A B \right) + \left( A B \right)[/math] [math]\frac{r B'}{A} = B \left( x^2 \frac{P}{\rho c^2} + 1 - \frac{1}{A} \right)[/math] [math] = B \left( \epsilon x^2 + 1 - \left( 1 - \frac{1}{3} x^2 + \frac{k}{x} \right) \right)[/math] [math] \approx B \left( \epsilon + \frac{1}{3} \right) x^2[/math] making the simplifying assumption of Schwarzschild (seemingly)... these equations quickly become quite complex and cumbersome [math]dP = \frac{\rho}{2} \frac{dr}{r} \sqrt{A} B \left(\epsilon + \frac{1}{3}\right) x^2[/math] [math] \approx \frac{\rho}{2} \left( \epsilon + \frac{1}{3} \right) \left( x dx \right) \sqrt{\frac{1}{1 - \frac{1}{3}x^2}} [/math][math]\left( \frac{1-\frac{R_S}{R}}{1-\frac{R_S}{R}\left(\frac{r}{R}\right)^2} \right)^{\frac{1+3 \epsilon}{2}}[/math][math]\times \left( 1 - \frac{R_S}{R} \right)[/math] but [math]R_C^{-2} \equiv \frac{8 \pi G \rho}{c^2} \approx \frac{3 R_S}{R^3}[/math] so [math]x^2 \equiv \left( \frac{r}{R_C} \right)^2 \approx \frac{3 R_S}{R} \left( \frac{r}{R} \right)^2[/math] and [math] dP \approx \frac{\rho c^2}{2} \left( \epsilon + \frac{1}{3} \right) \left( x dx \right) \times[/math][math] \frac{ \left( 1-\frac{R_S}{R} \right)^{\frac{3+3\epsilon}{2} } }{\left(1-\frac{R_S}{R}\left(\frac{r}{R}\right)^2\right)^{\frac{2+3\epsilon}{2}} }[/math] [math]= \frac{\rho c^2}{2} \left( \epsilon + \frac{1}{3} \right) \left( x dx \right) \times \sqrt{1 - \frac{R_S}{R}} \times[/math][math]\left( \frac{1-\frac{R_S}{R}}{1-\frac{R_S}{R}\left(\frac{r}{R}\right)^2} \right)^{\frac{2+3 \epsilon}{2}}[/math] [math]= \frac{\rho c^2}{2} \left( 1 + 3 \epsilon \right) \left( \frac{R_S}{R} \right) \left( \left( \frac{r}{R} \right) d\left(\frac{r}{R}\right) \right) \times \sqrt{1 - \frac{R_S}{R}} \times[/math][math]\left( \frac{1-\frac{R_S}{R}}{1-\frac{R_S}{R}\left(\frac{r}{R}\right)^2} \right)^{\frac{2+3 \epsilon}{2}}[/math] the obvious limiting cases would be [math]\epsilon = 0,1[/math], for which the function can be plotted, as an approximation, for the full solution, for which [math]\epsilon(x)[/math] varies w/ radius [math]dP = \frac{\rho c^2}{2} \left( 1 + 3 \epsilon \right) \left( \frac{R_S}{R} \right) \sqrt{1-\frac{R_S}{R}} \left( y dy \right) \times \left( \frac{1-\frac{R_S}{R}}{1-\frac{R_S}{R}y^2} \right)^{\frac{2+3 \epsilon}{2}}[/math] to lowest order in RS, and for [math]\epsilon = 0[/math], the equation defaults to a common classical HSE [math]\longrightarrow \frac{dP}{dr} \approx \frac{G M \rho}{R^2} \frac{r}{R}[/math] which is the isothermal sphere equation [math]\rho \propto r^{-2}[/math]... otherwise the equation seems easily integrable, by substitution [math] u = 1 - k y^2[/math]

if Z0 bosons can pair produce neutrinos & antineutrinos... and if photons are related to Z0 bosons... then can photons possibly pair produce neutrinos & antineutrinos ?

if photons have angular spin momentum (which i understand to be distinct from plane of polarization)... then do photons also have a corresponding magnetic moment ? (the only way i know of, to get angular momentum out of an EM field, is to combine an electrostatic field, with a magnetic dipole field... then the resulting field has angular momentum, in the magnetic-axis direction, Lz ~ z * (r x (E x B)) ... so, does a photon have some small magnetic moment, whose propagation with the super-imposed plane-wave EM field, accounts for the angular momentum of photons ? what generates Lz is the axially-directed field lines of B, crossed with radial E... so the angular momentum, of an oscillating E, varying perpendicular to the magnetic axis, might be possible to make to have axial angular momentum)

the solution can be computed exactly, for constant density [math]A(x) = \frac{1}{1-\frac{1}{3}x^2 + \frac{k}{x}}[/math] [math]x \equiv \frac{r}{R_C}[/math] [math]R_C^{-2} \equiv \frac{8 \pi G \rho}{c^2}[/math] said solution must be matched, at r=R, to the exterior solution, which defines the constant of integration k. Plotting said solution shows that, similar to the suggestion of Schwarzschild, the spatial stretch factor does decrease inwards

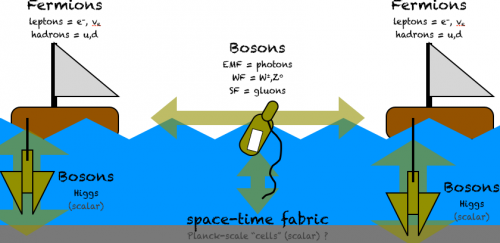
PXP => no two particles, in exactly the same state, in the same space... if there exists a "w", "in-out", hyper-thickness to the fabric of space-time... and if Fermions are full spin-1 Bosons, half of whose spin is directed thru the hyper-dimension "w"... (again, S2 = 1 = Sw2 + Sxyz2 = (1/2)2 + (sqrt(3)/2)2 = 1/4 + " (S=1/2) x (S=1/2 + 1) "...) and if that hyper-spin determines matter / antimatter... Sw = +1/2 = positrons & positron-neutrinos = antimatter Sw = -1/2 = negatrons & negatron-neutrinos = matter then the extrapolated-PXP would imply, that two positrons, or two negatrons, could not "stack"... but, one neutrino could stack w/ one electron (say)... those are different particles, different particle states, different wave-functions... and Weak-interactions involve neutrinos and electrons, not (to my knowledge) pairs of electrons, although i guess their could be neutral current interactions... i'm simply saying, that the fringes of wave-functions could conceivably begin to "stack" hyper-spatially, in fairly-flat-thin-land analogy similar to checkers, or a pair of burgers on a grill, stacked so that the edge of one was resting on the edge of the other, but not fully doubled up... the Weak-interaction can be interpreted, as regular run-of-the-proverbial-mill, EM interaction... through the hyper-dimension "w", when pairs of particles begin to double-stack hyper-spatially... the "Weak hyper-charge" is regular run-of-the-oft-mentioned-mill electric charge, aiming into the hyper-dimension (whereas "electric charge" couples into the standard spatial dimensions "xyz"). The neutrino has no "electric charge", i.e. its qx = qy = qz = 0... but it has "weak charge", interpretable as qw = -e... so the neutrino is "blind" to standard spatial displacements "xyz"... but when it wanders "into-and-under" or "into-and-over" another wave-function, it suddenly starts interacting intensely, other-wise-normal-electro-magnetically, through the hyper-dimension "w", apparently at "point blank range" ~10-18m = range of Weak-force = thickness "dw" of space-time... so i predict, that because the neutrino possesses some electric charge... neutrinos also generate some magnetic moment... whose magnetic dipole-esque field-lines try to point hyper-spatially through "dw"... but which "arc over" at the "top & bottom" of space-time, and re-direct through the three standard spatial dimensions "xyz"... i predict, that the "Higgs force", between quanta within the fabric of space-time, and space-time itself, is ultimately a grand-unifiable-example, of "the" one-and-only "grand unified force"... so the reason why neutrinos evidence nearly no "resting" mass-energy... is because they only "see" a short ("dw" long) sliver, of the fabric of space-time... owing to neutrinos only having hyper-spatially-directed charge qw = -e... neutrinos notice nearly no space-time -- only the vertical "hyper-section" of space-time exactly at their own spatial position "xyz" and only atto-meters thick "dw"... so they are barely attracted into the fabric of space-time, by the "Higgs force" = "EM force between quanta in space-time to-and-from space-time"... so, on that set of assumptions, i predict that neutrinos generate a magnetic moment, of magnitude, relative to electrons... comparable to the mass of the neutrino, relative to electrons... i.e. ~10-6 x ue again, neutrinos only "know" the one-and-only-grand-unified-force = "EM/W/S forces (thru space-time) between particles (w/in space-time)" = "Higgs force between particles and space-time itself"... neutrinos only know that force, through the hyper-spatial "thickness" dimension "dw"... so they have nearly no interaction w/ the fabric of space-time => nearly no mass because they also have nearly no "one-and-only-force charge" (only qw > 0) => nearly no magnetic moment (and nearly no interactions w/ other particles either) seemingly, astronomy could answer whether neutrinos possess any magnetic moment > 0... accordingly to the following powerpoint presentation in pdf, electron-neutrinos can emit W+ bosons, becoming electrons... if so, then perhaps neutrinos can in fact "flip hyper-spin" in intensely energetic interactions http://nucla.physics.ucla.edu/sites/default/files/NeutrinoMagneticMoment_2012Nov8.pdf the following figure attempts to depict an explanation for the forces at work in the world... EM/W/S forces, through the fabric of space-time, in between pairs of particles w/in the fabric of space-time... and the Higgs force, from those particles, to the fabric of space-time, itself... in analogy, particles are a little like boats... force-carryiers are a little like bottles between boats... and Higgs bosons are a little like anchors from boats to the bottom...

attempting to combine and comport the conventions, of page vs. page, [math]B \longrightarrow -B[/math] [math]U^{\alpha} = \left( \begin{array}{c c c c} \frac{c}{\sqrt{B}} & 0 & 0 & 0 \end{array} \right)[/math] [math]U_{\alpha} = \left( \begin{array}{c c c c} \frac{-c}{\sqrt{B}} & 0 & 0 & 0 \end{array} \right)[/math] [math]g_{\alpha \beta} = \begin{bmatrix} -B & 0 & 0 & 0 \\ 0 & A & 0 & 0 \\ 0 & 0 & r^2 & 0 \\ 0 & 0 & 0 & r^2 sin^2(\theta) \end{bmatrix}[/math] [math]T_{\alpha \beta} = \left( \rho + \frac{P}{c^2} \right) U_{\alpha} U_{\beta} + g_{\alpha \beta} P[/math] [math]T_{\alpha \beta} = \begin{bmatrix} \rho c^2 B & 0 & 0 & 0 \\ 0 & P A & 0 & 0 \\ 0 & 0 & P r^2 & 0 \\ 0 & 0 & 0 & P r^2 sin^2(\theta) \end{bmatrix}[/math] [math]T = T^{\alpha}_{\alpha} = Trace( g^{-1} T ) = \left( - \rho c^2 + 3 P \right)[/math] [math]RHS = \left( \frac{8 \pi G}{c^4} \right) \left( T_{\alpha \beta} - \frac{T}{2} g_{\alpha \beta} \right)[/math] [math]RHS = \left( \frac{8 \pi G}{c^4} \right) \begin{bmatrix} \frac{\rho c^2 + 3 P}{2}B & 0 & 0 & 0 \\ 0 & \frac{\rho c^2 - P}{2}A & 0 & 0 \\ 0 & 0 & \frac{\rho c^2 - P}{2}r^2 & 0 \\ 0 & 0 & 0 & \frac{\rho c^2 - P}{2}r^2sin^2(\theta) \end{bmatrix}[/math] [math]LHS = \begin{bmatrix} \frac{R_{tt} \times (-1)}{4 r A^2 B} & 0 & 0 & 0 \\ 0 & \frac{R_{rr}}{4 r A B^2} & 0 & 0 \\ 0 & 0 & \frac{R_{\theta \theta}}{2A^2B} & 0 \\ 0 & 0 & 0 & \frac{R_{\theta\theta} sin^2(\theta)}{2A^2B} \end{bmatrix}[/math] [math] \left( R_{tt} \times (-1) \right) + R_{rr} = 4B \left( AB \right)' = \left( \frac{8 \pi G}{c^4} \right) \left( \rho c^2 + P \right) \times \left( 4 r A^2 B^2 \right) [/math] [math] \left( AB \right)' = \left( \frac{8 \pi G}{c^4} \right) \left( \rho c^2 + P \right) \times \left( r A^2 B \right) > 0 [/math] Within material objects, space-time is "contractile" (with the words written by John Archibald Wheeler), as you move outward from the center of the object, the four-volume of space-time "voxels" [math]dV_4 = \sqrt{A} \sqrt{B} \; cdt \; dr \; r^2 d\Omega[/math] increases. [math] R_{\theta \theta} = r \left( AB \right)' + 2 A B \left( A - 1 \right) - 2 r B' A = \left( \frac{8 \pi G}{c^4} \right) \left( \rho c^2 - P \right) \left( r^2 A^2 B \right)[/math] [math] 2 A B \left( A - 1 \right) - 2 r B' A = \left( \frac{8 \pi G}{c^4} \right) \left( - 2 P \right) \left( r^2 A^2 B \right)[/math] [math] B \left( 1 - A \right) + r B' = \left( \frac{8 \pi G}{c^4} \right) \left( P \right) \left( r^2 A B \right)[/math] [math] B + r B' = \left( \frac{8 \pi G P}{c^4} \right) \left( r^2 A B \right) + \left( A B \right)[/math] [math] \frac{1 + \frac{r B'}{B}}{1 + \frac{8 \pi G P}{c^4} r^2} = A[/math] HSE: [math]\frac{dP}{ds} = - \rho g[/math] [math]dP = - \rho \left( - \Gamma^{r}_{tt} \right) dr \frac{ds}{dr} = \rho \left( \frac{B'}{2 A} \right) dr \sqrt{B}[/math] which would seemingly bring about an integro-differential equation, for a self-consistent solution, even for the simplified situation, of incompressible constant density. Schwarzschild seemingly assumed (see below) that the space-time within a massive object, of constant density, would manifest closed constant curvature: [math]B \equiv \frac{1}{1 - \left( \frac{r}{R_C} \right)^2}[/math] If so, then [math]B' = B^2 \left( 2 \frac{r}{R_C^2} \right)[/math] [math]x \equiv \frac{r}{R_C}[/math] [math]A = \frac{1 + 2 B x^2}{1 + \frac{8 \pi G P}{c^4} r^2} = \left( \frac{1 + x^2}{1 - x^2} \right) \frac{1}{1 + \frac{8 \pi G P}{c^4}r^2} [/math] Now [math]R_C^2 = \frac{R^3}{R_S}[/math] so at the surface of the massive object [math]x^2 = \frac{R_S}{R}[/math] and the pressure P = 0, so [math]A® = \frac{1 + \frac{R_S}{R}}{1 - \frac{R_S}{R}} \ne 1 + \frac{R_S}{R}[/math] of the exterior solution. So the assumption of Schwarzschild seems (slightly) in error. Still, his interior solution (see below) appears, plausibly, to be qualitatively correct. Note, that time totally stalls out, into static stasis, inside the center of some massive object, which becomes compresses & compacted down, to R = 9/8 RS. So, according to the interior solution of Schwarzschild, once some star collapses & compresses, to 9/8 RS, its center stalls out into a stasis of timelessness. Per that picture, space is strewn w/ stars, which are technically still in the process of continuing collapse... but which infall will require infinite time to actually occur (as seen from afar). If so, then there are not actually any "black holes" anywhere within the fabric of space-time... all "complete collapses" stall out into timeless stasis, before full infall actually occurs (as seen from afar = HST). Note that the low-gravity limit, of the gravitational acceleration, according to Schwarzschild's interior solution, is g® ~ r, which is the field from an isothermal sphere, with density decreasing as r-2. So i know not where Schwarzschild derived his interior solution... still his has the advantage, of being continuous through the surface of the object, and so seems qualitatively correct. http://www.rafimoor.com/english/GRE3.htm http://en.wikipedia.org/wiki/Geodesics_in_general_relativity http://cr4.globalspec.com/blogentry/17100/Spacetime-Curvature

http://en.wikipedia.org/wiki/Deriving_the_Schwarzschild_solution i tried re-deriving the Schwarzschild solution from the above, recouping the original R_ii terms (in the derivation above, the R_ii have been multiplied by factors vaguely resembling (4A2B, 4B2A, and 2A2B2). Then i set the SET to T_tt = rho c2, all the rest zero, assuming that time is orthogonal to xyz <----> r theta phi, so that the change of spatial coordinates does not affect the T_tt term in the corner (according to common convention, not the wiki article). Then i used your dual equation: http://blogs.scienceforums.net/ajb/?p=934 and tried to calculate the interior solution, for a spherically symmetric, constant mass-energy density ball... now the RHS <> 0, and no more is AB = const... combining all the equations, i got B = stuff involving A's in numerator and denominator then i assumed, that A® = dr2 coefficient = 1/sqrt(1 - kr2) = constant closed curvature = cosmology... then everything simplified, and B = 3/4 (approx.) actually B = pi rho R3 / M (approx.) which i think varies between 1/4 to 3/4 depending on the compactness of the object (dense objects stretch space more, and can pack more mass, for the same density, within the same coordinate radius) but anyway B ~= 1 (of order) so i essentially recouped FRW cosmological metric, for closed curvature (B=1, A=1/sqrt(1-kr2)). such seems surprising... immediately above a compact object's surface... space is stretched to near-tearing (and time "thins out" to preserve AB=1, i.e. space-time volume is preserved, space stretches, but time thins out)... but then immediately under said surface, time is nearly normal, and so is space, the stretchings and contractings are only of order 1... if you consider the Flamm's paraboloid, above the object, space is super-stretched... but w/in the body, space is only "bowed down" slightly... a diameter through the object ought to have a length 2R, but (assuming constant curvature) now stretches to pi*R = 50% increase = of order one... the following figure is qualitatively accurate, in conveying the concept, of constant closed curvature w/in the body, but (potentially) arbitrary spatial stretch above-but-near its surface... http://cr4.globalspec.com/PostImages/201202/general_relativity_curved_space_time_sta_7A21E635-A1DF-6F5B-F2C7D945567BFAE0.jpg so, is that a potentially plausible solution for a Schwarzschild-interior ?? in low-orbit above the body, time-and-space dilations are enormous... but inches under the same's surface, things are nearly normal ?? The above solution matches the spatial curvature, at the object's radius, from the Flamm's paraboloid curve above the body, to a constant closed curvature w/in the body... but how would one handle the discontinuous jump, in time ?? Time ticks super-slow just above the body, but nearly normally w/inside the same ?? That would require lines-of-simultaneity to jump discontinuously,

the exterior Schwarzschild metric is "four-volume preserving", i.e. space stretches, but time compresses, such that (c dt) dx dy dz = [math](c dt) r^2 dr sin(\theta) d\theta d\phi[/math] = constant trying to take the Trace or determinant, and observing cancelations of crucial coefficients, is essentially the same, as noting that the warping of space-time about the body is "four-volume preserving", space stretches, but time "thins out", preserving the over-all (four) volume, a little like a piece of putty stretching in one dimension, but thinning out in orthogonal directions, preserving the overall volume of putty

hyper-spin commutation relations would basically break down as Sw x Sxyz... the hyper-spin Sw defines particle / antiparticle, and is "pinned" (with want of worthier words)... if anything could flip hyper-spin, 'twould be Weak-bosons, in intense "point blank" Weak interactions (interpreted as when particles start to "stack" hyper-spatially, (partially) occupying the same xyz, but "stacking" in w, so as to be blasted, at "point blank" range, by hyper-high energy interactions)

(oops) [math] \boxed{ F_w = - \left( G_4 m \rho_4 \right) W} [/math] Note that [math]dm = dV_4 \rho_4 = dV_3 \Delta w rho_4 = dV_3 \left( \Delta w rho_4 \right)[/math], so that the perceived 3D mass-density of space, is the product of the actual 4D hyper-density, and the 4thD hyper-thickness, of the fabric of space-time.

thin thickness of space-time fabric => Higgs potential If the fabric of space-time is fully 4D, and if a particle is attracted, to every "cell" of the space-time fabric, with a hyper-force... then if that particle strayed away from the hyper-mid-"plane" (= 3D volume at hyper-planar-center of 4D-but-thin space-time)... then that particle would be pulled back towards the hyper-mid-"plane"... by a force proportional to its hyper-displacement [math]\Delta w[/math]... which would be described by a potential proportional to the square of its hyper-displacement [math]\frac{1}{2} \Delta w^2[/math]... which describes the quadratic Higgs potential, of the Higgs field (the quanta of which are the Higgs bosons), as described in Riccardo Barbieri's Lectures on the Electro-Weak Interaction... Proof: The differential 4D force, of attraction, between our particle (of mass m), and some "cell" of the space-time fabric, is [math]d \vec{F}_4 = \frac{G_4 m \rho_4 dV_4}{2 \pi^2 R^4} \vec{R} = \frac{G_4 m \rho_4 dV_4}{2 \pi^2 R^4} \begin{bmatrix}{c} x \\ y \\ z \\ w-W \end{bmatrix}[/math] By spatial symmetry, all of the spatial components (Fxyz) cancel. For, for every four-voxel of 4D space at (say) x, another at -x produces precisely the same magnitude of x-force, but in the opposite direction. Thus, seemingly sensibly, this 4-force never pushes particles spatially, through the fabric of space-time... particles never acquire "sudden impulses of momentum magically". Thus, we only consider the hyper-spatial 4-force component Fw. [math] F_w = \int dF_w = \left( \frac{G_4 m \rho_4}{2 \pi^2} \right) \int dw dx dy dz \frac{w-W}{\left( x^2 + y^2 + z^2 + \left( w - W \right)^2 \right)^2} [/math] Since the hyper-dimension is orthogonal to all three standard spatial dimensions, and by symmetry of standard space, the triple-standard-spatial integral can be converted, into 3D spherical coordinates: [math] = \left( \frac{G_4 m}{2 \pi^2} \right) \int dw \int 4 \pi r^2 dr \frac{w-W}{\left( r^2 + \left( w - W \right)^2 \right)^2} [/math] [math] = \left( \frac{ G_4 m}{ 2 \pi^2 } \right) \left( 4 \pi \right) \left( \int_{W}^{W_{max}} - \int_{W_{min}}^W \right) \left( \int d\chi \frac{\chi^2}{ \left( \chi^2 + 1 \right)^2 } \right) [/math] where one re-scales the standard-spatial-radius coordinate, into units of the hyper-spatial-displacement distance, which requires breaking the hyper-spatial integral into two pieces, according to the sign of the hyper-displacement (w-W). Then, the re-scaled, dimensionless, [math]\chi[/math] integral, by variable substitution [math]\chi \equiv tan(\theta)[/math] simplifies into the integral of [math]\int sin^2(\theta) d\theta = \frac{\pi}{4}[/math]. So, [math] F_w = \left( \frac{G_4 m}{2 \pi^2} \right) \left( 4 \pi \right) \left( \frac{\pi}{4} \right) \left( \left( W_{max} - W \right) - \left( W - W_{min} \right) \right)[/math] Since space-time is assumedly symmetric, hyper-spatially, Wmin = - Wmax, et ipso facto [math] F_w = \left( \frac{G_4 m}{2} \right) \left( - 2 W \right) [/math] [math] \boxed{ F_w = - \left( G_4 m \right) W} [/math] Thus, hyper-displacements, away from the hyper-mid-"plane" of space, would experience restoring forces, proportional to that hyper-displacement, which is equivalent to a quadratic potential, equivalent to the proposed potential, of the Higgs field.

thin thickness of space-time fabric could account for electrons' anomalously large magnetic moments If space is fundamentally 4D = xyz+w, then fundamental forces are 4D. Then, fundamental forces would decrease, over 4D hyper-distances, as 4D field-lines dispersed, over the 3D hyper-surface-areas, of the 4D hyper-spheres, surrounding some force-field-line-generating particle, at a particular point (xyzw) in 4D space. The volume of a 4D hyper-sphere is [math]V_4 = \frac{\pi^2}{2} R^4[/math] so the 3D hyper-surface-area of such is [math]S_3 = \frac{\partial}{\partial R} V_4 = 2 \pi^2 R^3[/math] Thus, 4D force-fields would be [math]\vec{F}_4 = \frac{G_4 m}{2 \pi^2 R^3}[/math] i.e. the particle generates [math]G_4 m[/math] field-lines, which disperse & spread out, over hyper-surface-areas. Now, if the fabric of space-time is 4D, but very thin, in the hyper-dimension "w", then those field-lines could be constrained, to "arch over" and "bend down", from the "hyper-poles" of those hyper-surface-areas, to the "hyper-equator", so as to remain within the thin fabric of space-time. If so, then those [math]G_4 m[/math] field-lines, emerging from some particle, would actually only disperse & spread out, over a radically reduced hyper-surface-area: [math]\vec{F}_4 \longrightarrow \frac{G_4 m}{\left( 4 \pi R^2 \right) \times \Delta w} = \frac{G_4}{4 \pi \Delta w} \frac{m}{R^2}[/math] So, we can quickly identify [math]\frac{G_4}{4 \pi \Delta w} \longrightarrow G_3 = 6.67 \times 10^{-10} N m^2 kg^{-2}[/math] However, if field-lines could disperse away into surrounding hyper-space (the "Bulk" of String-Theory), then the number of field-lines captured, within the thin fabric of space-time, would simply decrease "normally" (from 4D hyper-spatial perspective): number of field-lines captured = [math]\frac{G_4 m}{2 \pi^2 R^3} \times \left( 4 \pi R^2 \Delta w \right)[/math] field-lines per perceived standard-spatial surface-area = [math]\frac{G_4 m}{2 \pi^2 R^3} \frac{4 \pi R^2 \Delta w}{4 \pi R^2}[/math] which decreases as distance cubed, far faster than any known fundamental force (i.e. gravity, electro-magnetism). Ipso facto, force-field-lines could be constrained, to "compress down" and remain inside the fabric of space-time, unable to disperse away, through higher dimensions, into hyperspace. Et ergo, if electrons actually are full spin-1 particles, then they actually have twice the spin now known, and so would generate twice the magnetic moment... all of whose magnetic field-lines would "twist over", constrained to remain within the fabric of space-time, so that although half of their mechanical angular momentum is "hidden in the hyper-dimension", all of their electro-magnetic moment "twists over" and projects into-and-then-through the fabric of space-time.

Fermions with "hyper-spatial spin" pointing "out" (say) = matter = "pan-cake right-side up on griddle" pointing "in" = anti-matter = "same pan-cake but upside-down on griddle" matter + anti-matter = (+1/2) + (-1/2) = 0 = Boson = photons this simple picture explains anti-matter as the "flip-side" of matter; and explains why when M+AM collide, the result = Bosons w/ no "hyper-spin" Fermions have angular & linear momentum in the hyper-spatial dimension; Bosons have neither angular nor linear momentum in that "w" dimension (from Rudy Rucker's convention) (i've revised my speculation -- i think that there is a common unified "electro-weak-strong" force, for interactions between particles w/in the fabric of space-time... its "currency" = charge... and another force, for interactions between all of those particles, and all of their force-carrying kin... to the fabric of space-time... its "currency" = mass-energy)

Photons have an intrinsic angular momentum, pointing parallel or anti-parallel to their path of propagation, with a magnitude of exactly one unit of h-bar... yes? Thus, when electrons emit or absorb photons, they must spin-flip, which represents a change of -1/2 hbar <----> +1/2 hbar = one unit of h-bar... yes?

if space-time "grips" photons, such that the cosmologically expanding fabric of space-time stretches photons propagating through said space-time => red-shift ... then would a contracting fabric of space-time compress photons => blue-shift ? Further, what about astronomical red-shifts / blue-shifts, brought about by the time-varying expansion / contraction of the fabric of space-time, near to super-massive / super-dense compact objects ? As they "dance" around each other, in intense interactions, would the fabric of space-time stretch as they sped past, and then contract as they moved on... and would photons flying through said space-time fabric be "astronomically" red-shifted / blue-shifted ?

[math]\frac{\sqrt{3}}{2}[/math] commonly occurs, in conjunction, with 30-60-90 right triangles... that number so suggests its orthogonal compliment, [math]\frac{1}{2}[/math]... and a spin of 1/2, orthogonal to the three standard spatial dimensions (xyz), suggests a fourth "hyper-dimension" (w), parsimoniously interpreted, as a "small" dimension, being the "thickness" of the fabric of space-time, i.e. the "thickness of the rubber-sheet of Flatland" in down-dimensioned analogy. Again, i re-propose, that the exact same lines of logic, allow parsimonious interpretation, of rest-mass, as momentum directed through a dimension (w) orthogonal to the three standard spatial dimensions (xyz), E2 = m2 + p2 = pw2 + pxyz2 Professor Rudy Rucker (Geometry, Relativity, Fourth Dimension) wrote, that the fabric of space-time, may have a "hyper-thickness" (w), rather than actually really truly having zero thickness, and being infinitesimally thin. Such seems patently implausible -- the fabric of space-time spans billions of light-years in numerous other dimensions, curving around through a higher hyperspatial dimension. A "small" but non-zero thickness certainly seems much more plausible, and parsimoniously explains rest-mass as "hyper-momentum" (momentum directed hyper-dimensionally, "across" the fabric of space-time); non-interger-quantized spin, as the "spatial half" of integer spin values; "color" as axial orientation. -------------------------------------------------------------------------------------------------------- that rest-masses, of the three "flavors", of up-quarks, as functions of the "flavor" number (n=1,2,3), quite closely follow: m = 2 n10 Thus, the "fourth flavor", which according to this hyper-spatial hypothesis, is the "first ionized" state, would be predicted to occur, at an energy, of approximately 3000 GeV = 3 TeV. Thus, i would offer, from this hyper-spatial hypothesis, that at energies of order 3 TeV per quark = 10 TeV per nucleon, physicists would witness "magic moments", wherein matter, in ultra-high-energy collisions, "vanished" from the collision chamber, leaving no traces. At such super-high-energies, matter might be "blasted off of the Flatland fabric of space-time", out into hyperspace, "ionized" out of the hyper-spatial potential well, within which all mass-energy, embedded within our fabric of space-time, resides. Conceivably, matter "blasted out into hyperspace" might gradually "rain back down onto the fabric of space-time" elsewhere, perhaps far from the original collision location. If so, then perhaps the centers of cloud-chambers would remain pristine... and then, some moments after the collision, matter might spontaneously "poof (back) into the fabric of space-time", way out at the edges of the cloud-chambers (or something similar).

Fermions (s = 1/2) have a total magnitude, of angular momentum, directed through the three standard spatial dimensions (xyx) of [math]S^2 = \hbar^2 s\left(s+1\right)[/math] [math] S = \hbar \sqrt{s\left(s+1\right)} = \hbar \frac{\sqrt{3}}{2}[/math] Such suggests, that spin-half Fermions have another half-unit of spin, directed through a fourth, "hyper" spatial dimension (w), of the "thickness" of the fabric of space-time. I.e. Fermions are actually four-spatial-dimensional quantum wave-functions, having a total actual magnitude of angular momentum, equal to one unit of [math]\hbar[/math]: [math]S^2 = \hbar^2 = S_w^2 + S_{xyz}^2 = \hbar^2 \times \left( \left( \frac{1}{2} \right)^2 + \left( \frac{\sqrt{3}}{2} \right)^2 \right)[/math] By comparable calculation, Bosons (s = 1) have a total angular momentum, directed spatially, of [math]\hbar \sqrt{2}[/math], suggesting that they are actually spin-2 particles, having half of their spin directed hyper-spatially: [math]S^2 = \hbar^2 = S_w^2 + S_{xyz}^2 = \hbar^2 \times \left( \sqrt{2}^2 + \sqrt{2}^2 \right)[/math] -------------------- i re-propose, that the three "colors" of quarks actually represent three standard spatial axial orientations of quarks; and that the demand for "color neutrality" is actually a requirement for "tri-axial omni-directionality" of the quark triplets, making up nucleons. Quarks have four charge coupling "slots", which can be activated (+/-), or deactivated (0), said slots representing the coupling, of quarks, into the four spatial-and-hyper-spatial dimensions (xyz+w). For instance, a proton, composed of two up-quarks, and one down quark, could exist in the following detailed "fempto state" Similarly, a neutron could be composed of: u = (+,+,0,-) d = (-,0,0,-) d = (0,-,0,-) ---------------- n = (0,0,0,-) For comparison, electrons: e = (-,-,-,-) and neutrinos: ve = (0,0,0,-) Gluons resemble W+/- in that they carry away charge, i.e. charge coupling constants, from one quark, to another: W+ = (+,+,+,0) W- = (-,-,-,0) g1 = (+,-,0,0) g2 = (+,0,-,0) g3 = (0,+,-,0) g4 = (-,+,0,0) g5 = (-,0,+,0) g6 = (0,-,+,0) From the above, one can clearly comprehend, that those gluons "toggle" quarks, from one axial orientation to another; and do so, in such a way, that their absorption by another of their fellows, also "toggles" them, from the other orientation to the one: u = (+,+,0,-) ----> (+,0,+,-) + g3 u = (+,0,+,-) ----> (+,+,0,-) - g3 d = (-,0,0,-) ---------------- p = (+,+,+,-) Quarks only couple, by the one-and-only-grand-unified-force, into one, or into two, spatial dimensions... they are observed, macroscopically, from far far away, averaged over long long time spans, to have "fractional" charges, only because, as they spin and tumble and roll around every which way, spatially, they only couple into those directions, on average, one-third (or two-thirds) of the time. By analogy to the common "color" model, quarks can "fake out" and "feint" their fellows, by the emission of "axis - anti-axis" gluons (in the color model, called color-anticolor, e.g. red-antired): g7 = (+/-,0,0,0) g8 = (0,+/-,0,0) g9 = (0,0,+/-,0) u = (+,+,0,-) ----> (+,+,0,-) + g7 or 8 or 9 u = (+,0,+,-) d = (-,0,0,-) ---------------- p = (+,+,+,-) such "psyched-you-out" gluons represent quarks beginning to "toggle"... but then "thinking better of it" and reverting back, to the way they were, originally. For complete clarity, the "axial orientation" of up quarks is defined, by the standard spatial axis which lacks a charge coupling; and of down quarks, by the standard spatial axis which actually contains a coupling. Due to the need for constant tri-axial omni-directionality, when one quark begins to "extrude" or "emit" or "emanate" a gluon, carrying away some of its charge(s), to another of its fellows, then the other quark "must must must" absorb the whole entire gluon, head-to-tail, so flipping into a complementary orientation, before the first quark "lets go" of its gluon. If, during that exchange process, one or the other (or both) of the quarks is "kicked" by a hard nuclear interaction, then the "extruder" can be "gripping" the tail of its gluon, while its fellow is "gripping" the head of the same gluon -- when the exchange is suddenly rudely interrupted, prematurely. Such can cause the gluon to "stretch and rip and tear", producing pions: uz = (+,+,0,-) ----> (+,0,+,-) + (0,+,-,0) ----> (0,+,0,+) + (0,0,-,-) = !dy + dz uy = (+,0,+,-) dx = (-,0,0,-) ---------------- p = (+,+,+,-) The proton partners are "left in the lurch", with two mis-(parallel-)aligned up quarks, and several down (and anti-down) quarks, two of which constitute a pion. Violent processes then sort out the mis-matches. Note, that nucleons are highly "hyper-charged"... unlike charge neutrality of atoms, in the three standard spatial dimension, every quark is equally charged, in the fourth hyper-dimension, such that all nucleons have --- = -1e unit of charge, focused in the hyper-spatial "w" dimension... and the addition of all of an atom's electrons only exacerbates the hyper-charge accumulation, in close confines -------------------- The fabric of space-time has a hyper-spatial thickness, approximately equal, to the range of the Weak interaction (~10-18m = 0.001 fm), which represents the range at which wave-functions begin to "stack up over each other" through that "thickness" in the hyper-spatial "w" thickness dimension. The three "flavors" of fundamental Fermions represent the three bound states, of Fermions, in the potential well, created by the two parallel hyper-surfaces, of the fabric of space-time ("the wafers of the ice-cream sandwich"). As evidenced by the top quark, that potential well is ~200GeV deep. Since there exists only one single grand-unified force, and since quantum wave-functions of Fermions are attracted into the fabric of space-time by their interaction with its "hyper-potential", such implies that the hyper-surfaces, of the fabric of space-time, are charged. Further, since charged matter, and anti-charged anti-matter, both bind into space-time, with (nearly) identical energies, symmetry suggests, that one hyper-surface is positively charged, and the other negatively. I.e. the fabric of space-time is similar, to a dielectric gel, between the two parallel plates, of a capacitor. Now, those hyper-surfaces are the 3D surfaces, of 4D space (xyz+w)... every point in space (xyz) is bound "out" and "in" by two other points (xyz +/- dw). From known numbers, one can estimate the value of the forces involved: Volts = Joules / Coulomb = 200GeV / (1/3e) = 600 GV (three units of charge, one each in x+y+z, is perceived as "one" unit of electron charge; matter only carries a single unit of charge, coupling into the fourth, hyper-spatial, "thickness" dimension, "w")

http://en.wikipedia.org/wiki/Grain_boundary_strengthening http://en.wikipedia.org/wiki/Stress_intensity_factor the yield strength of many materials depends upon the sizes (D) of the grains comprising the sample, [math]\sigma = \sigma_0 + \frac{K}{\sqrt{D}}[/math] that is the same mathematical dependency, as the stress occurring w/ cracks, of length L, [math]\sigma \approx \frac{K}{\sqrt{L}}[/math] logically, grains = "bricks", and the amorphous material "mortaring" them together = "mortar" the characteristic size of the bricks and surrounding mortar could conceivably set the scale of size of cracks inside the sample, somewhat similar to bricks cracking loose from their surrounding mortar, in a brick wall, most cracks become about as big as the bricks... except would be in 3D inside some crystal lattice seemingly, supposing that the size scale of the bricks & mortar, sets / limits the size scale of cracks, could account for both processes... the amorphous mortar, and also the mis-alignments between bricks, contains cracks inside grains... and the grains block the propagation of cracks, down through seems of mortar, between the faces of opposite grains, when the cracks try to propagate out to the sides, for then they "run into" the sides of other grains... the dis-order of the mortar and mis-alignments from grain to grain, block the propagation of dislocations within the ordered lattices inside grains... and the order of the grains, blocks the jagged faults w/in the mortar grain hardening seemingly plausibly represents "crack containment" w/in the crystal lattice http://en.wikipedia.org/wiki/Carbon_nanotube if so, then by analogy, crack containment could be crucial, in carbon-fibre cables... stronger carbon cables could conceivably be composed, of multiple types of "zig zag" & "arm chair" and other "m,n" configurations of carbon tubes... such that cracks occurring in one, would be contained, by the atomic mis-alignments, of its carbon atoms, w/ those of adjacent fibers... although the separate-ness of the separate fibers could conceivably already contain cracks into single fibers

the mass excess, of 2p > p:n = D = H2, is ~0.9 MeV. But the EM force => p:p is unstable... logically, ergo, the EM positive potential energy > 0.9 MeV i.e. EM energy of interaction ~MeV or greater MeV EM interaction could create electron-positron pairs

logically, the crystal lattice of some sample specimen straining under tensile stress, is a little like a long "chain of hands", atoms "gripping nearest neighbors" when the lattice is stressed, some atoms wind up having a "firmer hold" of the "hands" to one side or another... some of the lattice atoms on one side of the mid-plane will actually become pulled towards the other side... et vice versa opposing sets of "chains of hands" lie along each other, and slide past each other, towards opposite poles of the stress apparatus as they slide past each other, they would induce shear-like tensions in each other (and their flow would seemingly somewhat resemble viscous fluid-like flow) if you stopped the stressing, and sawed the specimen in half... then you would see what you could conceivably call "dislocations" in each smoothly sawed face... those "dislocations" would actually have been "locations" connected to the crystal lattice in the other half (they would, then, "line up" when the halves were placed face to face) the more dislocations per cross-sectional area, the more viscous-like-fluid-flow-forces of shear would have been opposing the pulling at some point, during "necking down", the "last in the lines" of the "chains of hands" would slip past each other, at failure inter-penetrating portions of the crystal lattice, pulled oppositely past each other (on nano-to-micro-scopic scales), inducing shear-like viscous-resembling force effects, could common-sensically account, for the equations with-on Wikipedia