-
Posts
916 -
Joined
-
Last visited
-
Days Won
3
Content Type
Profiles
Forums
Events
Everything posted by martillo
-
I was wrong in that statement and I admitted it well correcting the thing. I after said that conductivity is actually accomplished in solid metal conductors by the absorption with posterior emission of photons in a process that has a time delay involved and so on and we have a long discussion about. I'm wondering why you aren't you considering all that now. By the way, I know I make mistakes sometimes but always try to correct them.
-
You know, you are wasting our times with silly questions what shows you really don't take enough attention in what we are discussing. The discussion is becoming useless now this way. I never said there is no conduction. I agree in heat transferring by conduction, convection and radiation. I think your idea about what I think is wrong in something. I maintain total agreement with the mathematical definitions of those concepts. If the cup is filled with hot coffee it doesn't stay cool, it warms with T superior to the environment T. Depending on the cup considered it warms more or less but it warms and if the cup is not a so good insulator its radiation can be sensed by finger or face at some proper distance.
- 222 replies
-
-2
-
Good question. Something I also thought about at some time. What I know is that's the way Enthaply is defined anywhere. P = F/A so F = PA and W = F.distance then PV = W makes sense but at in a perfect equilibrium both P and V are constant so no work done isn't it? I think the right anser could come considering the following: Thermal equilibrium is a dynamical equilibrium. In the case of the term PV you can think in the environment continuously doing an infinitesimal work on the system and the system continuously reacting with a correspondent infinitesimal work. You can think the environment winning in some infinitesimal areas of the surface while the system winning in the other infinitesimal ones. I didn't arrive to the right conclusion to finalyze the answer giving the not zero term PV in the equation. Something yet needs to be reviewed and solved in that subject. Well, as I already said I could agree on "atomic and molecular vibrations" present although we could differ in what we really mean by vibrations, how energy is stored in them and how they are provoked in atoms and molecules. No, radiation involves a gradient of temperature so the phenomenon is not isothermal. No, radiation is not transferred, heat (Q) is transferred. Radiation is dQ/dA. You are right that when we touch the cup conductivity takes place but if not touch no conductivity ad the cup remains radiating heat which can be felt with the face as I mentioned. There is air flowing upside and this case involves convection but I wasn't thinking in my face up the coffee cup. I was thinking in looking at the cup horizontally. We are thinking in different experiments then. Horizontally at some proper distance I can feel the radiation of the coffee cup. What idea are you referring to? Please explain.
-
Radiation is heat energy transfer rate. The rate of transmission is what makes the difference for my fingers "burn" or not. You can have lot of heat energy but transmitted at small rate then it would not affect too much while if it is transferred at a high rate it will affect ("burn"). I can feel the coffee radiation even with my face at some distance. More the distance less it affects of course.
-
There are two phenomena related to heat transmission. One is the velocity of the photons in a material dense medium. This is described by the refractive index of the material which relates the average velocity of the photons in the material in relation to the vacuum velocity c. At the Wikipedia page of refractive index (https://en.wikipedia.org/wiki/Refractive_index) you can also see how the refractive index varies with the wavelength in the "Typical values" and the "Dispersion" sections of the page. The other phenomenon is about the time needed to heat a piece of a material, is about hotness and our sensorial perception of hotness. Let us consider the case of a cup of coffee. We fill a cold cup with hot coffee. It takes some perceptible time for the cup to be heated as we can sense it with our fingers. This phenomenon is related to the capacity of the material to absorb heat, to absorb the photons. When we fill the cup it takes some time to its external surface to be heated what is what we can perceive with our fingers. The cup is being heated from its internal surface and it begins to absorb some small percentage of the radiation. While absorbing the heat radiation the heat does not reach the outer surface. The heat reaches the external surface when all the atoms of the thick wall of the cup were already heated. Only after we can sense then that the cup is hot and so we perceive the phenomenon as the heat of the coffee lates some time to propagate through the wall of the cup from the internal surface to the external surface. I hope to have been clear in my explanation.
-
Ok, just give me a little time now. I did some quantification. I talked about the enthalpy equation H = U + PV balancing the energies in the system. As evidence for the presence of photons in the system I mention that the Kinetic Theory predicts the total energy for an ideal gas to be H = (3/2)NKT (K is Boltzmann constant) while for solids the total energy is 3NKT. I think the Kinetic Theory is right here including the vibrations energy in the system among the kinetic energy of the particles (due to movement of their center of mass). Is missing then to consider the other half of the total energy in the case of ideal gases. The total energy must be the addition of the kinetic energies of the particles plus the energy of all the photons present. My theory predicts that for the ideal gases exactly the half equal to (3/2)NKT is missing and is related to the photons present in the system. In my model the total energy of the system is H = 3NKT and is equal to the total heat that was absorbed by the system to reach the considered thermal equilibrium, H = Q.
-
Trying to summarize the real point of our discussion: The Kinetic Theory explains Temperature as produced by the motion of material particles only. I said that there are photons involved which would be being ignored by the Kinetic Theory. I have commented I'm working on a model where the energy of those photons strongly contribute to the temperature of the system and you are trying to debunk it. You know, I'm realizing now that the concept of molecular vibrations is totally compatible with the presence of those photons. The atoms just would store the energy of absorbed photons in the form of vibrations in the atomic binding of protons with their electrons. That is also compatible with the discrete levels of the possible energies in the atom considering vibrations in a possible discrete set off possible modes of vibration. My model can be compatible with that. What I would disagree is if the photons are ignored and only translations in the center of mass of the particles are considered.
-
I looked in the site that publish that graphics and found the page where it is shown the Transmission curves for several glasses compounds: https://rmico.com/support/tech-notes/material-data. It can be seen the glasses sharply losing transmission capability in a range from 5 to 20 microns. That means that some glasses well transmit "light" while transmitting "heat" with different capabilities. May be there are glasses that well transmit EM radiation in the "heat" spectrum but would be not the case of the common glasses we use at our home windows on which we easily observe they transmitting "light" but not "heat". I'm losing the real subject of all of our discussion. Can you please summarize it?
-
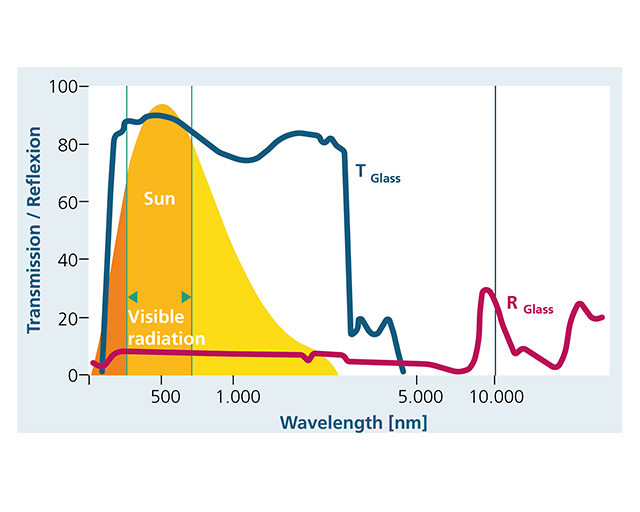
I have found what I needed,an interesting site (https://www.ist.fraunhofer.de/en/newsletter/answers/can-glass-reflect-heat.html) talking about glass transmission of EM radiation and present a very illustrative typical graphics of the transmission capability of the radiation by glasses varying with the wavelength of the incident radiation in the blue line in a logaritmical scale. It well shows how there is a sharp lose of that capability on the range between 1000 nm (1 microns) and the 10000 nm ( 10 microns) which is precisely the range @swansont presented in his link. It shows how glass stopped transmitting sharply at about the 3000 nm (3 microns) and so how glasses is transparent to "light" while an becomes an insulator for "heat". It also talks that the mechanism involved in the transmission is about absorption, emission and reflection of EM radiation as I sustained. So my approach about material particles (atoms/molecules) storing EM radiation in the form of photons absorption keeps up.
-
Let we see if the following is the right answer to the mess. We are looking at the problem with two views: 1) The relation of energy transfer with the temperature T. 2) How heat energy is transferred through some transparent but good insulator glass in terms of the velocity of propagation, the wavelength and the frequency of the incident heat. Case 1: The radiance is P/A where power P = ΔQ/Δt. ΔQ is the total amount of energy transferred between two bodies with different temperatures T1 and T2 (T1 - T2 = ΔT). A is some area of a considered surface for the transfer. P is the rate of transfer. Then: ΔQ = ∫12(PA)dT = A∫12PdT Now the problem is that in the Newton cooling formula is assumed a small difference in the temperatures for which P can be considered constant while in the general case it varies non linearly: If P = constant it is ΔQ = PAΔT If P not constant P = P(T) which is given by the the Stefan-Boltzmann law and is proportional to T4. Nevertheless the Thermodynamics laws can give the amount of ΔQ transfer for this case which result being linearly proportional to T. For a small difference in the temperatures this case falls into the Newton's case above. Case 2: The transmission of radiant energy by a glass depend on its frequency : a) Glass can absorb and emit in the "light" spectrum quite transparently (velocity of propagation inside the glass has a little difference with that in air (refractive index approximately 1). b) Glass quite cannot absorb in the "heat" spectrum and the small quantity it can transmit propagates at a slow velocity (refractive index is high much greater than 1). Note: I looked for technical data of this variation in the web but couldn't find a credited source.
-
.03 x 10-8 sec is the interval of time t. .02 m is the thickness d. v = d/t = .02/(.03 x 10-8) = (2/3)c in accordance with the refractive index n = c/v = 1.5. Not at all. What is the same is the velocity c. The frequency varies as the wavelength varies: f = c/λ. More attention please, if not is useless to discuss. In the reference it is said: "the heat transfer rate varies as the difference in the 4th powers of the absolute temperatures". I'm tired to say to you that heat transfer of energy rate is different than heat transfer of energy even with different units. I always stated: transfer of energy rate is proportional to T4. transfer of energy is proportional to T. So you are wrong to state "radiative heat transfer depends on T^4". Radiactive, conductive or whatever heat transfer depends on T (according to the Thermodynamics laws). And: whatever heat transfer rate is proportional to T4 (according to Stefan-Boltzmann law).
-
I think the real problem we have here is in which kind of "heat" is considered. One case is the infrared range as described in the link of "infrared optics" you provided. It is considered yet an "optical case" even in your link. So I would not call it "heat" range and yet call it "light" range, not visible but yet a "light" range would be more appropriated. Other case is yes the "heat" in the range which we can feel with our fingers for instance which is not an optical case at all. In this case much lower frequencies are involved and the glasses quite not transmit any "heat" and that's why they are good thermal insulators.
-
No it is .03 x 10-8 sec. No, I'm saying that in a material with refractive index of 1,5 heat takes .03 x 10-8 sec to pass through. The refractive index of glass for "light" is different from that for "heat". This strongly depends on frequency. From Wikipedia in the link you provided: "Another situation that does not obey Newton's law is radiative heat transfer. Radiative cooling is better described by the Stefan–Boltzmann law in which the heat transfer rate varies as the difference in the 4th powers of the absolute temperatures of the object and of its environment."
-
The velocity of propagation for an index of refraction is 1.5 is v = c/(1.5)c = 2c/3. The time is t = d/v where d is the thickness so for thickness = 2 cm = .02 m is t = .02/(2c/3) = .03/c = .03x10-8 sec. While the index of refraction remains the same this calculation remains the same so same time of propagation. λf = v is always verified so for each λ you just have f = v/λ just varying accordingly. For same index of refraction 1.5 it is same v = 2c/3 and so same delay of propagation t = .03x10-8 sec. No, the result is the same. What is different is just that I sustain that there are photons always present in the system (there would be a "photons gas" as is called). No it is not the S-F law that gives me a linear relation with T. I have already told you that "energy transfer" and "energy transfer rate" are different things with different units. The S-B law gives the "energy transfer rate" of the radiation through some area at some place proportional to T4 while the Thermodynamics laws give the total "energy transfer" between two bodies proportional to T. How many times I must repeat this?
-
In the link you provided the range of wavelength is about 1 - 10 microns but there is no mention in a change in the velocity of propagation. The velocity would remain the same. Why do you consider it varies? We have λf approximately c. While both λ and f vary accordingly the velocity remains the same: approximately c. May be there could be a little variation, I don't know exactly but there's no "10 orders of magnitude required for the heat propagation time to match the light propagation time" as you say. Your calculation is wrong. Well, Boltzmann solved it in "per unit area" basis and the Thermodynamics equations derived give a final linear variation of rate transfer in T. I stay with this. I already solved the thing this way. Now is that you want to solve the thing in a different manner, well, do it. You can't ask me to solve the things in your way. At the end we reach to the same result isn't it? As I said, you do it in your way. I already did it in my way and there is agreement in a linear relation with T. The discussion in this topic has ended for me. Just to mention, Newton's law of cooling works for small variations in T only.
-
I consider that once "light", "heat", any kind of EM radiation is recognized to be the radiation of a particle (flux of "photons") there is no need to consider a delayed action in the EM fields. I can think in the photons as an "electromagnetic particle" carrying an EM energy and an EM force. I can consider then instantaneous EM fields acting on travelling "electromagnetic particles". This means to abandon the "EM wave" theory of light and remain with an "EM particle" theory for light. This means to stay with the particles' model of protons, neutrons, electrons, neutrinos, photons but with instantaneous fields. The "force carriers" as "virtual photons" are not needed. This is the next step in my approach. With this approach the things get simplified a lot. Maxwell equations remain for the E and B fields, of course, but not the "EM waves" that simply would not exist. To be demonstrated, of course, what would fall in demonstrating that the E and B fields are instantaneous.
-
Is that I'm used to think with the classical physics approach. I'm reviewing concepts. In Particle Physics the EM force is carried by virtual photons. I mean, the Lorentz force is carried by virtual photons. The concept of a delayed action at a distance of a force is replaced by the concept of a "virtual particle" force carrier called a "virtual photon". The same but differently. To find the first experimental evidences of this delayed action I must go back to the years of Lorentz and Maxwell. The concept appears first while associating "light" to an EM wave, not to a particle. The concept of "light" as composed by photons particles comes with Planck and Einstein.
-
I appreciate the good lectures you provided on the subatomic particles. You know, the world of the subatomic particles under the basic level of the electrons, protons, neutrons, neutrinos and photons is something weird for me. hope I would not need to enter too much in the area but who knows if I would need to make an incursion at some time. I think one of the main reasons to introduce the mediators in the model of the elementary particles is the finite velocity c of propagation of the EM fields. A far as I know the experimental evidence for it was Hertz experiment about standing waves which allowed an experimental evidence for the existence of the EM waves. I want to ask you if there are other experiments demonstrating the finite velocity c of propagation of the EM fields or if it is the only one. I'm managing the possibility for them to actually be instantaneous. I have a new interpretation for the Hertz experiment in which what the antennas emit and absorb would be photons. This way what Hertz has detected would be intensity of photons and not waves. The same patterns of waves can be obtained this way, particularly the pattern of standing waves. Then, photons would do travel at the finite velocity c but the EM fields would be instantaneous.
-
As I said for the case of the prism, it is possible for the velocity of heat to be different at different frequencies. The velocity would be dependent on the frequency of the photons. This is not a problem in my approach since it only implies that the time delay in the absorption with posterior emission of the photons vary with the frequency of the photons.