martillo

Yes, but they do not apply this in the derivation of the thrust force. They just say: "The right-hand term depends on the characteristics of the rocket and, like the left-hand term, has the dimensions of a force. This force is called the thrust, and is the reaction force exerted on the rocket by the mass that leaves it." The net force on the rocket is just the thrust force. There's no other force considered.

Yes, equation 1.5. Right below they say: "The right-hand term depends on the characteristics of the rocket and, like the left-hand term, has the dimensions of a force. This force is called the thrust, and is the reaction force exerted on the rocket by the mass that leaves it."

There's something that have passed unperceived Physics that would severely affect it in many areas because of its consequences. Please read with attention, the problem was described with care. The real equation of force is F = ma Today's Physics is stating that the Equation of Force is F = dp/dt. We will analyze the equation of motion of rockets to see that the real Equation of Force is: F = ma A rocket has variable mass in its trajectory and it's important to see its motion equation. Let m be its variable mass at any instant in its movement composed by the mass of the rocket plus the mass of its contained fuel. I have made a search in the internet about rocket motion equations and all the sites agree in the equation: F = m(dv/dt) = –ve(dm/dt) where ve is the speed of the expelled fuel relative to the rocket. One web site: http://www.braeunig.us/space/propuls.htm They all agree that the force acting on the rocket is due to the expelled mass and is F = –ve(dm/dt) and that the equation of motion is F = m(dv/dt) = ma. I assume the equation have been completely verified experimentally with enough precision from a long time ago. It is evident that it is used the equation: F = ma for the force and not: F = dp/dt By definition p = mv and dp/dt = m(dv/dt) + v(dm/dt). They derive the rocket's equation of motion based on the principle of conservation of momentum but considering the momentum of the rocket with the totality of the fuel (the contained plus the expelled fuel) at any moment and stating dp/dt = 0. After that they derive the equation of motion of the rocket as: m(dv/dt) = –ve(dm/dt) and specifically say that the force on the rocket is: F = m(dv/dt) = –ve(dm/dt) m(dv/dt) = ma then it is clear that what is finally applied to the rocket to determine its movement is the equation F = ma and not F = dp/dt. This indicates that today's Physics is wrong stating the Equation of Force as F = dp/dt. The right Equation of Force is F = ma even when mass varies. Note that the natural derivation of the famous equation E = mc2 by Relativity Theory has no sense since it is based in the wrong relation F = dp/dt. Relativity Theory becomes a wrong theory since it is based on a wrong law. By definition: p = mv With partial derivatives: dp/dt = m(dv/dt) + v(dm/dt) Now as: F = m(dv/dt) then the valid Equation of Momentum and Force is dp/dt = F + v(dm/dt) Then the principle of conservation of the momentum p = mv must determine that dp/dt = 0 when no forces are applied and when there's no variation on the considered mass. It can be observed that this principle can be applied to the rocket as was applied in the cited cases giving the same result. Considering the mass m' of the composed body of the rocket and the total fuel (the contained plus the expelled fuel) which does not vary: F’ = 0 and dm'/dt = 0 then the thrust equation can be derived (as below): m(dv/dt) = –ve(dm/dt) where m is the mass of the rocket with its contained fuel. Finally: F = ma = m(dv/dt) = –ve(dm/dt) is the force exerted on the rocket. F = –ve(dm/dt) Rocket thrust force derivation The thrust equation of the rocket is derived here considering the approximation that the mass of the expelled fuel of the rocket is negligible compared with the mass of the mass of the rocket plus the mass of its contained fuel: Momentum and Force equations: p = mv, F = ma = mdv/dt dp/dt = mdv/dt + vdm/dt = F + vdm/dt Considerations: a) masses equations: m = mass of the rocket with its contained fuel me = mass of the expelled fuel m’ = m + me = constant = total mass of the system rocket with total fuel dm’/dt = dm/dt + dme/dt = 0 Then: dme/dt = -dm/dt b) velocities equations (one dimension): v = absolute velocity of the rocket ve = velocity of the expelled fuel in relation to the rocket assumed constant u = absolute velocity of the expelled fuel ve = v – u = constant dve/dt = dv/dt – du//dt = 0 Then: du/dt = dv/dt Derivation: Total momentum of the system rocket with total fuel: p’ = 0 p’ = mv + meu = mdv/dt + v/dm/dt + medu/dt + u/dme/dt Considering: du/dt = dv/dt and dme/dt = -dm/dt p’ = (m + me)dv/dt + (v-u)dm/dt As v – u = ve and considering me << m (m + me ≈ m) then: p’ ≈ mdv/dt + vedm/dt and as p’ = 0 then: mdv/dt ≈ -vedm/dt Finally F = ma = mdv/dt ≈ -vedm/dt under the approximation me << m Then the rocket thrust force is: F ≈ -vedm/dt

That's it. Thanks! (+1) By the way... If you find this stirring wait for the next thread of mine...

And you succeeded. My calculations were wrong. I admit it now. Any acceleration. Gravity, vehicles' accelerations, whatever. I think time dilation and length contraction exist as observed on different frames in Relativity Theory but also the relativity of simultaneity. I'm thinking the things could run such a way that different aging is something that could actually not take place ever. I mean, as Genady said some at some post, the timestamps in the clocks of each traveler is always the same so aging actually would not actually take place. That's what happens in the problem we analyzed with constant velocities and no acceleration so valid between inertial frames only. Now I'm speculating on the possibility that something similar could happen with accelerated frames. Just speculating with the idea now. As Markus Hanke said there's some experiments showing time dilation in accelerated frames but may be, just may be, aging could be something different that could actually not take place in this case too may be due to the relativity of simultaneity. I mean time is affected by accelerations but simultaneity too and so may be the timestamps (clocks' readings) could always be the same...

Thinking that is not the case now. The discussion in this thread made me change my mind. I'm convinced now that in the case we analyzed the travelers don't age differently at the end. Actually I'm thinking that may be just travelling at high velocities does not produce any difference in age ever except possibly for the case of accelerations present and this is case for pure GR theory which is an area I don't pretend to enter. That's what some physicist are arguing now, that the difference of age is caused by the accelerations only. Actually my problem was with the idea of travelers aging less and the idea has vanished now. I'm speculating now that may be in some future is demonstrated that also accelerations actually would not produce any difference in age and in all cases the twins will reunite with the same age. That's what I'm thinking now. The twins' paradoxes would be solved at the inverse now: that at a first approach in Relativity Theory travelling twins could age less while actually that is not the case.

Yes, the diagrams, Genady and Lorentz Jr have shown me that. Is not that I don't want it to be, I just want the real thing. That is why I considered for instance beards in the twins as a way to show that the times showed by the clocks is not so relative as some ones use to think. They must match and this goes against the intuitive notion of the other twin aging less. I know Physics does not need to be intuitive and can give counterintuitive results, I just wanted to be sure about this subject. Is something I need to process on my own way now, no other way. Someone telling me that it is just that way is not enough. I need to refute my own intuition with some proper arguments... I appreciate your meaningful advices. They prevent me to make several mistakes. The problem is that I'm working in some other very important subject for me and it needs attention too. Some things take time, you know. I think could be another important subject to discuss here in this forum where I have already found the very right answers other times. Important subject and not only for me, I think. May be I post something soon, I don't know...

Yes, it would be much better.

The good thing of this is that calculations can be made with the space-time diagrams just with geometrical considerations. I think that was intuitively the approach in my calculations although making some things wrongly of course. I will try to remake them some day and if I find something to discuss may be I post a new thread about.

I edited the post above: I looked for that on google and found that if the frame is inertial then the length between two points on the lines represent the elapsed time between the events in the frame. Link: https://phys.libretexts.org/Courses/University_of_California_Davis/UCD%3A_Physics_9HB__Special_Relativity_and_Thermal_Statistical_Physics/2%3A_Kinematics_and_Dynamics/2.1%3A_Spacetime_Diagrams The above is right then because the travelers are moving at constant velocity v, not experimenting accelerations and so their frames would be inertial.

For v in units of c. Got it! 😄 The final question: can the elapsed times in each frame be obtained geometrically with the length on the lines of the travelers? I mean do the lengths on the lines represent elapsed times en each own frame? If so, the triangle B-D-F must be isosceles with base B-D and height to F which would mean equal times for B and C in their own frames. Or not? I looked for that on google and found that if the frame is inertial then the length between two points on the lines represent the elapsed time between the events in the frame. Link: https://phys.libretexts.org/Courses/University_of_California_Davis/UCD%3A_Physics_9HB__Special_Relativity_and_Thermal_Statistical_Physics/2%3A_Kinematics_and_Dynamics/2.1%3A_Spacetime_Diagrams The above is right then because the travelers are moving at constant velocity v, not experimenting accelerations and so their frames would be inertial.

Got it. Just one more question: would the slope in my diagram be to big? I mean the velocity of the traveler C must never be higher than light velocity: v < c. Seems to be right, the time axis is on the vertical and so Δx/Δt < 1 implies Δt/Δx > 1 for v in units of c.

Ok, here the diagram now: Thanks for the correction. I think I got it! It's just about the slopes of the lines of the signals... Thanks very much...

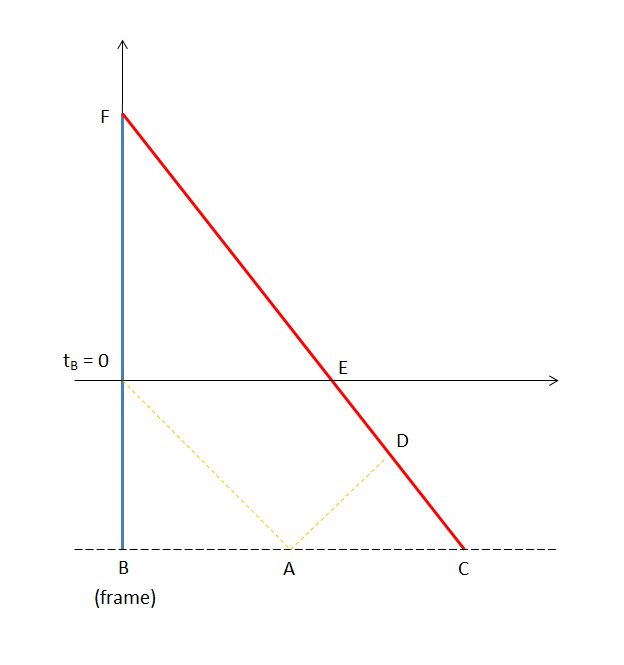
Thanks for the link, I will take a look. I think I'm understanding well enough the space-time diagrams now. Just one thing remains for me to understand in the twins paradoxes and is what you pointed out: dist(B,A) ≠ dist(A,C). I think is something I must study on my own now considering both, Lorentz transform and space-time diagrams to get the key points properly. I accepted the thing before but some postings later make me doubt and so I must study the subject deeper. I will do it but I will late some time of course. As for now here my diagram of the problem we were analyzing (Point A looks at the midpoint but it is not, I know now, it just should be near I think): The dashed black line at the bottom represent the initial time of the emission of the signals from A to B and C in frame B. Points D and E are the locations of traveler C (on line red) when he receives the signal and when traveler B (on line blue) receives the signal respectively. Any comment about is welcome. Designing the diagram made me understand some things better...

Sorry, I'm a bit tired and got confused again with an old bad concept. I need to have a rest now...

I see a visual problem in the diagram. The projections of the points onto the vertical axis shows the times of their events, right? Well, projecting point C to the vertical axis I see that the elapsed time to the final point will be bigger than the B point to the final point. This would mean the reading of the clock C bigger than that of the clock B (clock C > clock B) while it was supposed to be the inverse. Time would pass slower for C so his clock should show a smaller value (clock C < clock B). Seems this would happen whatever the values of v and distances would be considered. Am I wrong in something?

It's fine Lorentz Jr. I got a much better understanding of what is going on. I will try some calculations based on the diagram but I would late too much. May be in some future I could post a thread with the results to reevaluate things if necessary. I appreciate very much all this discussion and I hope it could have resulted positive for all of you too.

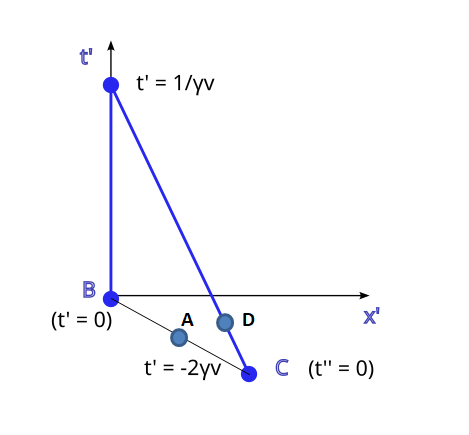
I think I'm getting it... Only the values doesn't match well: 1/γv << 2γv. If I look at the projections of the final point and the point C into the time axis they don't match well with those numerical values.

As md65536 posted, Lorentz transform are linear transforms preserving midpoints. A will always be the midpoint. He commented that distances and times would be different. I'm trying to view that.

It is just an intuitive location of events. I expect help to improve the diagram... May be I'm wrong I know... Right. I think the same. I thought that with just lines I could locate points A and D. May be I'm wrong.

I'm trying to locate points A (signal emission) and point D (signal reception by C) in the diagram. Is it so complex?

Well, I tried to improve Lorentz Jr diagram. Are the points A and D well situated or not? A will also belong to the midline between the lines of B and C...

Yes, you all have already told me that. I just showed my calculation to illustrate how to calculate X with a simple equation. I just want to know which values to use for the two distances. I thought I could deduce that with the help of the diagrams. Point D needs to be located and calculated...

No, please consider B always at X = 0 to match with the diagrams you and Genady have made. B is stationary, doesn't move. I'm assuming initially (time when the signals are emitted) and in B frame dist(B,A) = dist (A,C) = L. After sometime B and C receive their signals, B still at x = 0 and C at some point L + X where X as I calculated above. May be I calculated it wrongly as you said. I don't know why...

No, is the distance I'm assuming now in B frame. I don't use frame A...