-
Posts
916 -
Joined
-
Last visited
-
Days Won
3
Content Type
Profiles
Forums
Events
Everything posted by martillo
-
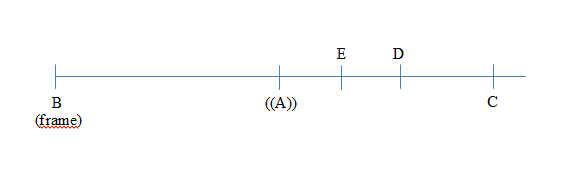
Well, that could be my problem. How would you find the distance (not the time) where C encounters its signal?
-
Point D : when C encounters the signal. Distance from A to D travelled by signal of synchronization of C : X = dist_B(A,D) which verifies: time_B(C,D) = (dist_B(A,C) - X )/v = (L – X)/v = time_B(signal(A,D)) = X/c Substituting values: (L – X)/v) = X/c X = Lc/(v + c)
-
Calculating: first I determine the distance at which it receives the signal. At some distance X of A the signal travels at c velocity and encounters traveler C who comes traveling from initial point C at velocity V. It just needed to solve a simple linear equation in X. Just give me some time to show it. Having the distances is just dividing by the velocity v to find the time traveled..
-
Right, C relative to B. This way it is not needed to use the relativistic addition of velocities I think. The movement of A doesn't matter to me, just its initial position when the signals are emitted from this point A matters.
-
I think it must be chosen the velocity that makes the calculations easier. At a first approach seems now, as we are working the problem now, would be to consider v as the relative velocity between the travelers. The velocity of the midpoint A doesn't matter to me. The intention is to compare just the observations between the travelers.
-
Good question. I will wait Lorentz Jr answer because I would prefer to maintain the convention of his calculations.
-
The velocity of the travelers.
-
You are right (me wrong). Genady's diagram must be reviewed to locate appropriately the travelers locations at the times of the receiving signals as you asked.
-
The problem in the calculations I made is that they do not cancel. Thinking about that now... I'm assuming t = 0 the time of the emission of the synchronizing signals from the midpoint to B and C. I think this matches with your diagram with B and C at the x axis at time t = 0.
-
Thanks very much. I expected that but wasn't sure. In the graphic the travelers B and C are initially at the x axis isn't it? I will think about the timings now... Taking into account the Lorentz transforms...
-
Well, this is what I must think in then... As designing time-space diagrams seems to me is easy for you, can you post a space-time diagram for the perspective of the traveler at B? I mean for the "stationary" frame attached to B. That is my approach. I think it would be interesting for everyone.
-
I'm still confused with some things... My reasoning without math: If someone has a clock running slower he will measure less time between two events than other one with a clock running faster. Well, consider two ones travelling to each other in uniform motion (without any acceleration). If the first event is two travelers at some distance and the second event is when they cross each other then one clock measures less and the other more. I don't understand how that cannot be true. But now imagine the two travelers shave their beards at the first event. When they cross each other they would present different beards because different time passed for each other. That is not real, they must present the same beard. Where am I wrong in this? I just tried to figure out the problem with synchronizing signals from the middle point to make the math with clocks but I only got to be more confused now. I would need time to rethink now. May be in some future in some new thread I could discuss this subject better, I don't know...
-
Glad to see that all the discussion left something positive not only for me but for you too. Thanks!
-
You are right Lorentz Jr, this is the main error in my calculations. There´s a gamma factor of proportionality in the transform between frames but there's also the translation of the moving frame. That was my big error. And everybody is right. I apologize for my error. I apologize Genady for not agreeing with you before. I couldn't see it. My error, my fault. I could see it applying the Lorentz's transform at the initial instant. It's all about relativity of simultaneity, something I didn't consider in the problem...
-
May be the second comment does not apply... I apologize. I got confused now. I think I need some rest now...
-
Well, I agree, I must review this in deep... I realized about other two problems in my calculations: 1) If v = (3/5)c then γ = 5/4 and not 3/2 as I used in the calculations. That's a bad problem of mine. I use to make silly mistakes in numerical calculations. I think it does not alter the conclusion of less time passing for traveler C but is an error... 2) I used: Δt = γΔt' but what appear everywhere is the inverse: Δt' = γΔt . I don't understand. If for example γ = 5/4 and the stationary time is 10 using Δt' = γΔt will give Δt' = 50/4 what would mean the moving clock running faster because showing a bigger time. I used the inverse relation in the problem. What do you think about? Do you mean the assumption dist_B(B,A) = dist_B(A,C) at the initial state of the travelers' problem is not correct for you?
-
Just separate the two things and focus just in the problem now. With the right assumptions is an easy problem to solve...
-
The movement of A is not considered in the problem. Is no necessary. Just the movement of C in relation to B matters. The only things that matters in A is its initial location where the emission of the synchronizing signals takes place. At the end C crosses with B at that location but as the three coincide the calculation is made for when C crosses with B what is what really matters. It could be unconventionally but precisely that is why it is simple to solve. I think you are mixing the way I solved the problem with the way I demonstrated the assumption dist_B(B,A) = dist_B(A,C) at the initial state to be correct. For this demonstration I used a frame centered at A for the Lorentz's transform to be applied in an easier way to show that an initial midpoint is preserved as a midpoint in the change of frames. In the problem of the travelers the frame of B is centered at the initial position of B. I think the same assumption is valid in both cases. Am I wrong in this? I have seen many times in the literature that for elapsed times, I mean for variations in time, it is valid: Δt = γΔt' All times considered in the problem are elapsed times so I think is right to be applied. Am I wrong in this? Good point to review...
-
No, in my problem there's just one stationary frame in B and a moving one in C. The only velocity considered is that of C in relation to B and I set it to be (3/5) of light velocity for a γ to be 3/2. No other velocity is needed to be considered. A is just the place where the synchronizing signals are emitted. At the end B and C reunite in that initial point A so to calculate when C reaches A is the same to calculate when C reaches B (independent of A) and this is what I do.
-
This are not the same assumptions I made for the initial state. This is a similar but different problem. In my problem the initial instant is that of the emission of the signals from A to B and C and in that instant B is located at -L and C at +L. B and C receive the signals at some time after when they set their clocks to zero. I consider just one stationary frame in B and a moving one in C. The reciprocal problem is just symmetric with symmetric results. It must be noted (as Genady pointed out) that in B stationary frame the traveler C receives the synchronizing signal before B because C is moving towards the initial place of A where the signal was emitted while B is not. This means that at the instant when B receives his signal (setting his clock to zero), C has already received its own before and so at that B instant the clock of B the time is greater than zero. I have expected from you something about a possible error in my problem as I formulated it. You come with another problem. I will try to understand this your problem and point out something if I could see some issue in your resolution but unfortunately the followers of the thread have now two different problems to analyze making the things much hard I think. That is not something good I think but I leave the other ones to decide which problem to stay with... NOTE: In my problem no velocity-addition formula is required to be applied. Is a much simpler problem I think. I don't switch frames...
-
-
The initial situation is when A at the midpoint emits the synchronizing signals to B and C. The clocks are arbitrary synchronized to 0 after when receiving the signals.
-
I find very appropriated your final comment: "I bet that SR could be figured out from scratch by amateurs using just the 2 postulates, some geometry, and the timing of light signals, if you're interested.." This is the way my calculations were made. It is considered the simple scenario of just two travelers B and C travelling in opposite directions to meet at the midpoint A. A is just the midpoint where the synchronizing signals are emitted at an initial time and is the final crossing point of them where A, B and C reunite. This is the specification of the problem to analyze. In my calculations I assumed the stationary frame of observation in B, the travelling one in C and I gave particular values to velocities and initial distances. I posted the calculations to discuss them if they were right or wrong and discuss posible errors. Genady pointed out that a possible problem in my calculations would be the initial assumption of A be a midpoint in frame B: dist_B(B,A) = dist_B(A,C) He said that would not be right and I disagreed. Let us consider now the Lorentz transform to see how the midpoint is preserved in the different frames: x' = γ(x - vt) t' = γ(t - vx/c2) Consider frame A with coordinates x, t and frame B with the coordinates x', t' in such a way that initially their origins coincide for the equations apply correctly. In frame A at the initial state of t = 0 we have: A at position x = 0, traveler B at some x = -L and traveler C at some position x = +L. Now in frame B by substituting values in the first equation of Lorentz transform we have: A at position x = 0, traveler B at x' = -γL and traveler C at x' = +γL We can see that A is preserved as a midpoint in the transform and my assumption would be correct then. I'm not saying all my calculations are correct, just that the initial assumption dist_B(B,A) = dist_B(A,C) is correct. I'm looking for other possible errors now but I cannot see anyone...
-
I wasn't a waste of time for me. I had a strong work based in your posts about the key points to consider in the problem which inspired me in a possible approach to the problem. I apologize to not be able to work with space-time diagrams appropriately. Unfortunately I arrived to something that doesn't match with some relativistic prediction and that is a big problem I know. You pointed out a possible error on which I disagree or just don't understand. I will continue reviewing and looking for my probable errors.