martillo

May be I didn't exprese the things properly. The factor γ appears in the calculations related to the time dilation effect. The relativity of time is considered in the calculations.

Well, let me say that my little expertise in space-time diagrams doesn't let me analyze them appropriately. I know they are two dimensional diagrams with the spatial axis and the timing axis and sometimes they can be worked separately as the projections of the events involved. My calculations are over the spatial coordinates only and seemed to be enough to find a solution to the problem, right or not, it shows it can be worked that way. As I already mentioned in a post I'm sure, by the specifications, that A, B and C are all travelling in a straight line with A as a midpoint always. This makes dist(B,A) = dist(A,C) always considering spatial distances. This mean a symmetrical travel in space. I don't understand how can there be a problem with that. I will continue reviewing the calculations thinking in what you said but I'm not sure to be able to work in the space-time diagrams appropriately as I said above.

Yes, I'm curious on the subject... 😄

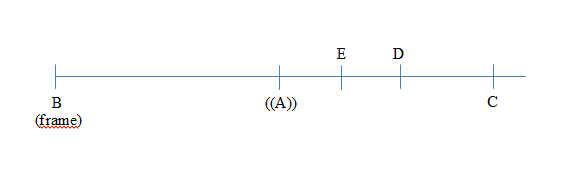
I have some of questions on the second diagram. 1) For me the diagram is related to frame in A because the vertical line passes through A. Now you are talking about B frame but still over the same diagram. I think in B frame the vertical line passes through B. I mean the space-time line of B would be vertical. 2) I'm not sure if the points P and Q you mention are related to the instant of emission of the signals by A or to the reception of the signals by B and C. Seems they are the points at the reception of the signals which I know that in the B frame do not happen at the same time. 3) I forgot the third... The third issue: What I know is that A, B and C are all travelling in a straight line with A as a midpoint. This makes dist(B,A) = dist(A,C) always at least considering spatial distances. This mean a symmetrical travel in space...

I'm getting it for now, I think...

Yes, right. The word didn't come to my mind... By the way, English is not my natural language...

Go on...

Right. You are considering frame A...

Let we try. I'm not very good with space-time diagrams but good to know your reasoning. Thinking now that the travel is spatially symmetrical in a straight line with A at the midpoint. This is spatially symmetrical. May be there is something asymmetric in time due to that in the frame considered of B, C is moving while B not... If we switch to the frame in A the travel is perfectly symmetrical in everything.

Thinking about... Seems to me now that the equality is valid always in the entire travel. I mean A moves such a way is always the midpoint between B and C in the entire travel. Why do you say this is not a symmetrical travel? I don't get it.

That counts in the initial state only. Just in the initial instant (when A emits the signals) dist_B(B,A) = dist_B(A,C). Not after of course. My fault is to have not commented that or to have not made it visible in the notation. The title of the paragraph says: INITIAL CONSIDERATIONS. I thought that was enough. Or is that this is not the point?

Well, here my calculations. I hope the notation would not complicate to follow the reasoning. The aim was to facilitate the understanding. May be I'm wrong in some thing(s) I cannot see. I would appreciate to be aware of them. RELATIVISTIC SYMMETRIC TRAVELERS INITIAL CONSIDERATIONS: B and C travelling in opposite directions to cross at midpoint A. They all reunite at the same position. It is considered a stationary frame with B. The case of frame in C is totally symmetric. A emit light synchronization signals to B and C : vel_B(signal) = c = 3x108 m/s Velocity of C in frame B: vel_B(C) = (3/5)c Relativistic factor γ = 1/(1-v2/c2)1/2 = 3/2 Relativistic relation of elapsed times: time_C = (1/γ)time_B Distances observed by frame at B: dist_B(B,A) = dist_B(A,C) = 3x108 mts D : point where clock of C is synchronized: clock_C = 0 E: point where clock of B is synchronized: clock_B = 0 CALCULATIONS: vel = dist/time --> time = dist/vel Times of signals travelling as seen by B and C : time_B(signal(A,B)) = dist_B(A,B)/c = 3x108/3x108 = 1 sec time_C(signal(A,B)) = time_C(C,E) = (1/ γ).1 = 1/ γ = 2/3 sec Distance from A to D travelled by signal of synchronization of C : X = dist_B(A,D) which verifies: time_B(C,D) = (dist_B(A,C) - X )/vel_C = (3x108 – X)/(3/5)3x108 = = time_B(signal(A,D)) = X/(3x108) Substituting values: (3x108 – X)/(3/5)(3x108) = X/(3x108) (5/3)3x108 = (1 + 5/3)X X = (5/8)3x108 mts Times of travelling of C from D to B as seen by B and C : time_B(B,D) = (3x108 + X)/(3/5)(3x108) = (1 +5/8)/(3/5) = (13/8)/(3/5) = (13x5)/(3x8) = 65/24 sec time_C(B,D) = (1/ γ)time_B(B,D) = (2/3).(65/24) = 65/36 sec Time of clock of C at the end of the travel: clock_C(B=C) = time_C(B,D) = 65/36 sec (65/36 = 1.80555555…) Time of clock of B at the end of the travel: (time from the initial situation to the end – time of synchronization) clock_B(B=C) = time_B(B,C) – time_B(signal(A,B)) = (dist_B(B,C)/vel_C) – 1 = = (2(3x108))/((3/5)(3x108)) – 1 = 10/3 – 1 = 7/3 sec (7/3 = 2.33333333…) CONCLUSION: Clock_C (B=C) < clock_B(B=C) These calculations conclude in a final lecture of the clock of C with a smaller value than the value of the clock of B what would mean less time passed for C than the time passed for B. FINAL NOTE: Just to mention here, the calculation of the lecture of clock of C at the synchronization of B (point E) gives the value ¼ sec and it was verified that adding this value to the time elapsed in the travel of C from E to B (time_C(B,E)) matches the value of the total travel of C in 65/36 = 1.80555555… sec. Each clocks start when the owner traveler receives the synchronizing signal from A. I wrote the calculations in Word and copied and pasted to the window of the post. Some emoticons appeared! For instance the C : without the space is replaced by a smile. I just edited that with a space.

Both doesn't matter for the calculations. They just don't appear. As I said (may be I was editing) the three A, B and C reunite in the same position at the end so, tu calculate the time of C travelling to A is the same as to calculate his travel to B. The travel of A doesn't matter, what matters is the relative travel between B and C.

I was editing while you posting. The moving A is considered as the emitter of the synchronizing signals and the final crossing point of the travelers where the three travelers A, B and C coincide in position. to say C travels to A or to B is the same since they will all coincide at the end. B does not emit the signals. The intention is to consider exactly the same posted case but just as observed by B only. I meant by lectures in the clocks as the time (timestamp?) the clocks show.

I just consider C travelling at some velocity towards A as A travels to B as seen by a stationary B and calculate what happens. I calculate the lectures in the clocks of B and C considering time = distance/velocity. Nothing else. A frame in C is a totally symmetric case. Frame in A is not considered at all. Just an emitter of synchronizing signals at A and the end point. The point of interest is how the travelers observe the things in the relativistic prediction. How the stationary one observe the things compared with how the relativistic prediction dictates the travelling one would observe. The stationary and the travelling clocks are compared. Just that. You are right I must take care about the velocities. I have found an error in that. I will late some time in the correction...

Right. I'm retired now and so anytime could e good for Physics now . I just follow my intuition. Sometimes I prefer the late advanced night when the city is very quiet and I can concentrate better... Thanks for the diagram. In my calculations I consider just one frame, the frame of B as the stationary and C travelling while comparing the clocks of B and C as observed by B. If the final lecture on both clocks were the same then there would be no problem, isn't it? The same time would have passed for both travelers since the synchronization. But as for now is not the case. I don't get what makes me reach different results with C aging less. I do not consider frame in A, I assume A just an emitter of the synchronization signals. The case of a stationary frame in C is just totally symmetric to the case in B. I worked hard in the night, making some final verifications now to type the calculations later.

But isn't expected in the relativistic prediction that the same time must pass (clocks' timing) in both twins after the receiving signal and reaching the midpoint? I mean, after they receive the signals they should age the same and have same beard. You said they present the same timestamp...

I'm not considering their "absolute" age but how they age after they receive the synchronizing signals from the midpoint. For instance I'm considering the twins could shave at the time of receiving the signals and compare their beards at the final crossing midpoint. Uruguay, UTC+3 If I'm not wrong. 21:42 hs right now. Night coming I know...

Good. I'm currently reviewing the calculations and I'm preparing something to post but I could late some time.

I'm working now in the solution to the case of the twins travelling in opposite directions without accelerations involved but with just a signal emitted from the middle point for clocks synchronization. I'm trying to make the calculations following the approach given by Genady (no Minkowsky diagrams) with some particular values for the velocity of the twins and the distance between them but I'm not getting the expected result. The ages does not match at the end. Is there any detailed calculation for this case available on the web that could help? I made my searches but couldn't find it.

Thanks for your clarifying explanations. I think the key point in the presented case is summarized in the statement: The timing variations in the clocks of the twins are strongly affected by their experienced accelerations at the turning back points. This case and the classic twins' paradox cannot be well explained without the considerations on the accelerations present. I remain wondering how they match perfectly with the time dilation effects but this would imply to enter in the area of General Relativity, something I do not pretend to do for now (I'm referring to the relation between clocks and accelerations).

I know, it just would affect his observations or calculations. Do you mean that the turning acceleration of B compensates exactly the timing effects in C of both, the travel plus the acceleration in the turning, for the twins finally cross at the midpoint with the same age?

Fine, let us retake the case as formulated first: Genady answered: I think now Genady considered here only the turn back of twin B aging less because of the acceleration in his own turning. Seems to me that the turning back of twin C would add the effect of less aging in C and they would not see the other one age the same at the end. B would observe C aged less at the end.

Seems to me now you have chosen a particular case of velocities for the twins. Seems to me that at other velocities the numbers don't match so well and it will be found the twins aging differently at the crossing point. Also seems to me you considered the twins' velocities as the same as the signals' velocities. If the signals are made of light this will bring the problem of travelling at light's velocity: time would not pass for them. Am I wrong in something?

Well, that would mean twin C begins to age earlier than twin B does. I must think about all this much more... Good question!