martillo

May be I need a new definition of temperature, I agree. I can perfectly define temperature based on the Stefan-Boltzmann Law Pot/A = σT4 which relates temperature with a radiation just considering this radiation as a radiation of photons. That is the well known kinetic to heat energy conversion. The classic Joule's experiment. Where is the problem? I perfectly agree with it. Temperature increase just means more photons emitted.

Show your case. May be the particles are immerse in the "gas of photons". Wherever exist temperature exist photons.

The answer is yes. I consider "heat" as the energy flow of photons what is the same as a radiation of photons. As I said other time, there is empty space between atoms and molecules where the photons can pass through. The average velocity of these photons would not be c as there would be scattering dispersion with the atoms and also absorption and re-emission of them in their not linear way. Conductive heat transfer is precisely this phenomenon of photons travelling through dense materials or substances. The phenomenon could be described as the progressive diffusion of photons inside them. I consider the cosmic background radiation as a radiation of photons particles. I'm considering the particles behavior of heat and light.

For those who could be interested in the new model I have proposed, with no vibrations in the particles (atoms/molecules of a substance), I think I have advanced in the direction of the energies' quantification. Of course the proofs of several (intuitive) assumptions made still remains to be accomplished. I show here just the straightforward quantification already developed only. I have considered: H = U + PV is the total energy supplied to the system considered at rest in a Thermal Equilibrium U = Er = Thermal radiation energy of the photons present in the system PV = Es + Ek where: Es = Energy stored in the electromagnetic structure of the substance (electrons' atomic levels and electrons' molecular bonding levels) Ek = Average Kinetic energy of the particles The Equi-partition Principle of the model would apply as: U = PV = H/2 = 3NKT/2 always So: H = U + PV = 3NKT always (K = NKb where Kb is the Boltzmann constant and N the number of the particles in the system) Depending on the nature of the substance of the system: PV = Es + Ek partitioned someway in Es and Ek Particular cases: 1) Ideal gases Es = 0 (negligible) Ek = 3NKT/2 Er = 3NKT/2 H = Er + Ek = 3NKT 2) Ideal solids Ek = 0 (static particles) Es = 3NKT/2 Er = 3NKT/2 H = Er + Es = 3NKT 3) Liquids Es + Ek = 3NKT/2 partitioned someway (depending on the nature of the substance) in Es and Ek -something between the cases of the ideal gases and ideal solids- Er = 3NKT/2 H = Er + Es + Ek = 3NKT As I already said, everything made just intuitively in the calculations must be yet proved valid. I will continue working forward on the subject as far as I could.

I don't know precisely with how much efficiently this system could be implemented. Anyway, I think it could have at least its appropriated applications. 2T motors are less efficient than 4T motors nevertheless they are used in some applications like motorbikes, chainsaws, grass cutters, etc.

I think the main advantage of this hydraulic transmission system stays in its extreme simplicity waiving lot of production costs. I know that also innovative designs in some of it parts would be needed to put it to work but the benefits well pay these things I think. Just to mention, I'm not interested in any possible patenting rights of the idea. Anyone can make completely free use of it if it where the case. That's why I'm posting it here. If by chance someone could actually be interested to know about the authorship he/she can just send me a personal message requiring the data. I tried to contact some people in the past having no feedback at all. My hope is that it could have useful applications somewhere and not just end lost in the bottom of the drawer.

It would depend on the efficiency of the hydraulic turbines/motors attached to the wheels, I know.

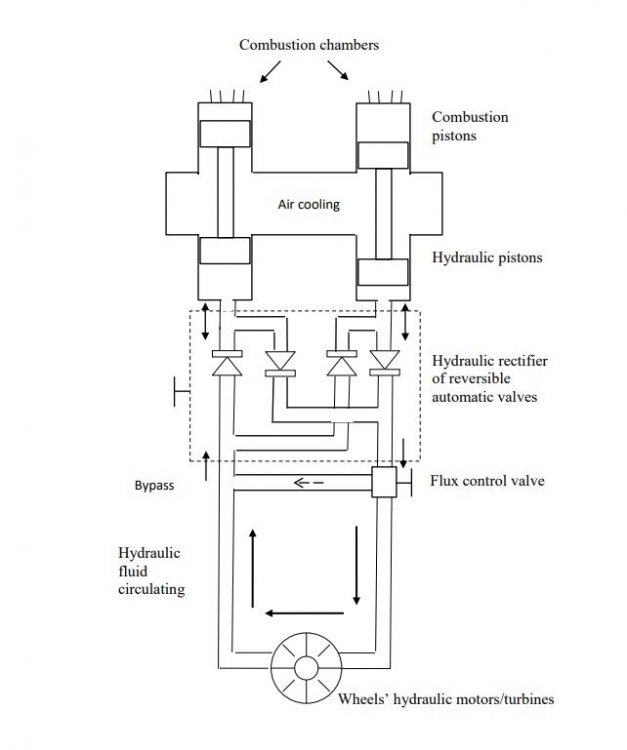
I have developed a very innovative combustion motor with a fully hydraulic transmission system. I'm posting here the diagram with a brief description I made to present it. The aim is to discuss potential problems and/or advantages it could have that I haven't seen on it. Any comment is welcome. Here is given a schematic description of a combustion motor with a simple but innovative hydraulic transmission system (based on an adaptation of an electrical device known as rectifier to hydraulics) which converts an alternating hydraulic flux to a “continuous” flux with automatic valves. The continuous hydraulic fluid would be directly transferred to hydraulic motor/turbine(s) to produce shaft rotational power. While on one side the hydraulic fluid descends and the other side ascends following the alternate sequence of the cycle of admission, compression, combustion and escape, a continuous flux of hydraulic fluid always moves in the same direction through the transmission line allowing the motor/turbines rotate the shaft(s). ALTERNATING MOVEMENT STABILITY: For the stability of the alternating movement of the pistons no flywheel is needed. Looking at the diagram it can be seen that the system with the hydraulic rectifier works fine in any configuration of the pistons. The force of combustion on a piston in any configuration will push it down and the hydraulic fluid will continue circulating always in the same direction. MOVING IN REVERSE: The solution is based in the design of reversible valves that could manually reverse the direction of circulation of the hydraulic fluid. In this case the motor/turbines would try to rotate in reverse with the hydraulic fluid circulating in the same direction. This provides also a way to brake the vehicle with the hydraulic motor. AUTOMOBILE APPLICATION FEATURES: _ In replacement of the conventional transmission and clutch flux control can be provided with the bypass line. _ If each wheel has attached its own motor/turbine no differential is needed. FIRST ADVANTAGES: _ Most of the mechanical parts of the conventional transmission of a combustion motor system are waived: crankshaft, freewheel, clutch, transmission box and differential. _ The overall propulsion system (motor + transmission) would weight much less with the obvious improvement in efficiency (less fuel consumption for automobile applications). FINAL NOTES: _ The motor of two pistons described in the diagram could work well in a 2T configuration with gasoline, diesel or even other fuels like hydrogen. It can work without a crankshaft and related mobile parts. In this case a motor starter must be developed and for motors with sparking an ignition system must also be developed. _ 4T motors could be developed with at least four pistons. They could be accomplished with two 2T motors just working in parallel over the same transmission line (simple connection to a unique hydraulic rectifier) and the four pistons synchronized with a crankshaft. Similarly, six pistons motors and more could be developed. _ Some small hydraulic turbine could move an alternator for battery charge.

As I have already said I have just begun working on the new model. I just don't have the quantification you are asking at this time. I told you I would do the calculation at the inverse: assuming the energy balance matches in the thermal equilibrium the number of particles emitting at some time could in principle be determined. What I perfectly know is that it is a total waste of time to try to convince you on the model. As I already told you, better for me to invest the time in developing the model further.

Yes I do have a model. I just don't have what you need to your calculation. That is not up to me after all. It is you that don't have any proof my model is wrong.

Seems to me that a block of solid copper is not a black body.

Not possible to know in advance, I think.

You added the same rate of energy emitted by all atoms to obtain the total radiation energy. That is wrong. The rate and number of emitting atoms to be considered makes the match in the balance of the internal and external radiation energies for the thermal equilibrium take place. Your calculation is wrong. I could refute all your posted arguments against my proposed model one by one although I know that would lead to an endless discussion. I'm sorry, I'm not able to do this at this time. I cannot continue the discussion. I must concentrate in developing the model further.

As you insist your calculations in your given case is right and for you to not think I didn't consider it properly I will point the main error. As I already said my proposed model must verify energy conservation of course. You begin calculating the number of atoms in the surface of the block of copper and for a given radiation energy you calculate the number of photons each atom must emit. In the second part you calculate the number of atoms in the entire solid block and calculate the energy of the radiation of all these atoms emitting the same quantity of photons. The error is in you are assuming all those atoms are emitting at the same time or in the same considered interval of time. How you can know in advance how many atoms do really emit at the same time? Nothing guarantees that. Actually the number of atoms emitting must be calculated considering that, at the inverse of your reasoning, both radiations the external one and the internal match to verify a thermal equilibrium state where a perfect verification of the balance in the radiations energies takes place. I conclude that as for now and having confidence in my reasoning (although aware of capable of making errors sometimes) my proposed model does have good chances. By the way... Doesn’t really matter; you still can’t reconcile the emitted radiation with the photon gas density you need to account for the thermal energy, since the residence time of the photons is so short. You seem to think that photons just disappear after some short period of time. You have mentioned this other times too. That is wrong. Photons don't just disappear. Photons don't just vanish. Whatever they are they have momentum and energy which cannot be simply lost or vanish. They can only be converted to other momentum and/or energy and this only happening in the interaction with some other existent particle(s) like the electrons for instance. May be you are confusing the behavior of photons with that of some virtual photons which for instance, like some other virtual particles, can randomly come in and out of existence. Real photons, as bosons they are, don't do that.

So what? For you absolutely nothing could be wrong in established Physics. For me is the established one but this does not prevent it for being wrong in something. As far as I know Physics as any other Science has never been totally infallible and there is a possibility I could be right in something. You mentioned sometime something like (my words because I don't remember it literally) that Physics' theories are essentially models of what happens in reality and they are considered valid ones while verifying the observational evidence. These are the established theories and I respect that. But what if another model appears also verifying the observational evidence? Then it just must show it can present a better agreement with some observations. Let me say now that I could be finding some such new model and I will work developing it as far as could. It would take time, of course, may be it would need the participation of other ones, of course, and actually there's no guarantee of success at this time, of course. This is not an impediment in my research for me. What I find at this time is that I must continue some research but not continuing this discussion in this thread now. I mean I could return at some time, I don't know, in this thread or another one, I don't know. I appreciate your comments very much but unfortunately we are in strong disagreement in some things and I cannot continue discussing now. My best regards.

It's your opinion and your decision. Seems other ones' too. I will continue further with my approach although not here in the forum. Thanks a lot for your comments, they have let me advance a bit while trying to give support to it. Best regards.

My reasoning is that the energy that is supplied to the systems we are analyzing comes in the form of electromagnetic radiation commonly called "heat" which is, in my understanding, entirely composed by photons. To begin I think in the "empty" cavity with totally reflective walls of a perfect black body is full of photons. It is under this assumption that Planck and Einstein derived their famous "Planck Law" of a black body radiation and "Planck-Einstein formula" E = hf. I then conclude that "heat" is actually composed by photons. The "heat" transferring between two systems is always through the interchange of photons which can pass through the walls separating them. Photons can pass through atoms and molecules (with scattering dispersion sometimes) carrying energy. Finally I consider that these photons come into the heated system and cannot just disappear. I can identify that part of them are converted into other forms of energy like the energy levels of electrons in the atoms and also other part is involved in the bonds between the atoms of the molecules. This energies compose the internal energy U in the equation H = U + PV. My claim is that the energy U is completely ignored in the called Kinetic Theory. In the Kinetic Theory we have U = 0 and H = PV = Kinetic Energy of the particles (translational motion in the ideal gases and vibrational motion in solids). I think that this is not what really happens in reality. As I said the incoming photons do not disappear and part of them is converted to structural forms of energies of the molecules, other part to their kinetic energy and other part just remains as photons in the internal thermal energy. As I said at some time I'm currently trying to take a mathematical account for how those are energies are distributed in the enthalpy H = U +PV equation. I think I advanced a bit in this direction: A system (solid, liquid or gas) is heated with an energy ΔH. Its internal energy U is incremented in ΔU = ΔStr + ΔRad where ΔStr is about the structural energy and ΔRad is about the thermal radiation. In agreement with Einstein I assume a possible increment Δm in the mass of the particles due to the absorption of energy being Δm = E0/c2 = ΔH/c2 as negligible and so the increment is in PV is Δ(PV) = ΔKE (the increment in the kinetic energy of the particles) . Then I have: ΔH = ΔU + Δ(PV)= ΔStr + ΔRad + ΔKE. I think now the Equipartition Principle applies here and so ΔStr = ΔRad = ΔKE = KT and I can have ΔH = 3KT in all cases, solids, liquids and gases. I just must mention here that for ideal gases we have ΔH = 3KT and not 3KT/2 in the generalized formulation of the Equipartition Theorem applied to ideal gases as it can be seen at Wikipedia page of the theorem: https://en.wikipedia.org/wiki/Equipartition_theorem . I'm yet still thinking in how the Equipartition Theorem is applied in this approach. I mean thinking in the physical considerations on the ΔStr and ΔRad energies for the Equipartition Theorem to apply.

When a system is in thermal equilibrium it has the same temperature in any place so the radiated power anywhere is also the same. The Power is the Energy emitted by the area of any radiating volume you can consider inside the system. Particularly a enough small one to identify it as a "place" in the system. The Power divided by the area gives the same value everywhere and it is the temperature in that place. Completely agree with this. Well, I'm currently developing (trying) a different explanation through a different cause for the phenomenon. I'm thinking in the photons continuously exchanged by the particles of a system with their surrounding environment. For instance, in a perfect black body of an empty reflective cavity the particles would be the molecules of the wall of the cavity where it can be considered the reflections the same as an instantaneous absorption and emission of photons.

I think something is not right in your calculation. You have a piece of copper radiating 2.75 W. If it is in thermal equilibrium the internal thermal radiation is the same as that external radiation of 2.75 W. That is 2.75 Joules per second. It is not about a kilojoule of thermal energy as you say.

Thanks. More clear now. You are talking about the vibrations approach.

For any material system, solid, liquid or gas an average temperature is maintained by the atoms/molecules which stay interchanging only some quantity of photons with the environment. Others are absorbed by them. Remember that after all the there's a lot of space between them. The surface to be considered is just a representative little "differential" area inside the system through which a "differential" quantity of photons are passing in two directions. I'm sorry but I cannot follow you in this. I don't understand the vocabulary properly and may be I'm not capable to put the subject in your terms.

Fine, if you can't manage my definition of the temperature for a single atom just forget it. My consideration that in the Kinetic Theory of Gases the internal thermal radiation is not taken into account still holds. As I said I'm considering https://en.wikipedia.org/wiki/Black-body_radiation particularly the following: The thermal radiation is described mathematically by the Stefan-Boltzmann Law: Pot/A = σT4 where Pot is the Potential of the radiated energy by unity of time. If the volume of gas cannot be considered as a black body it is just to make the appropriated correction in the law: εσT4 . The thermal radiation is an EM radiation (photons) and has momentum and energy. The main claim I'm pointing out is that in the volume of gas in a thermal equilibrium not only the atoms/molecules of the gas are present. There are photons in the volume with momentum and energy and they both contribute to the respective momentum and energy of the total system of gas plus photons in the volume everything counting for the total enthalpy of the system: H = U + PV If the system is externally heated in some amount there is an increment ΔH = ΔU + Δ(PV). The problem is in how the increment of this ΔH "heat" is distributed to the ΔU and Δ(PV) in the system. I tried a first mathematical account for everything together but I found it rather complicated for me and I'm not trying anymore for now. If I find something appropriated at some time I would return here. There would be less kinetic energy in the atoms/molecules of gas (with less average velocity) but this would not imply less temperature. It is compensated by an amount of temperature given by the photons according to the Stefan-Boltzmann Law.

From Enthalpy (https://en.wikipedia.org/wiki/Enthalpy) : Definition[edit] The enthalpy H of a thermodynamic system is defined as the sum of its internal energy and the product of its pressure and volume:[1] H = U + p V , where U is the internal energy, p is pressure, and V is the volume of the system; p V is sometimes referred to as the pressure energy Ɛp .[6] Physical interpretation[edit] The U term is the energy of the system, and the p V term can be interpreted as the work that would be required to "make room" for the system if the pressure of the environment remained constant. When a system, for example, n moles of a gas of volume V at pressure p and temperature T, is created or brought to its present state from absolute zero, energy must be supplied equal to its internal energy U plus p V, where p V is the work done in pushing against the ambient (atmospheric) pressure. The internal thermal radiation I'm considering (in its two models, EM waves or photons) has momentum and energy both contributing to the enthalpy. Its momentum contributes in the second pV term exerting a force and work while its energy contributes in the first U term the internal energy of the system.

That is a subject for another thread. You should open a new thread to discuss it.

I don't understand how it would be possible. May be something to discuss in other thread.