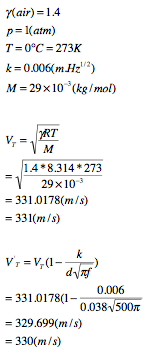Sarahisme

hi all , i can't figure out how i am ment to use the stated fact about tan x. the way i'd do it is dividing the series expansion for cos(x) into that for sin(x)... but yeah i dunno any advice would be greatly appreciated __sarah__

i can see that UnW must contain the zero vector that is in the vector space V, but this is only one of the three properties that need to be satified, and i am not sure how to show the other two properties (closed under addition and closed under multiplication) ??? ???

ok i am really stuck now, can someone please give me a hint? :S

ok thanks for that guys

yes but i think my way works aswell.... i think there are 2 ways to solve this problem....

oops sorry the problem! here it is.... (sorry about the blurriness)

hey i am not sure if i have done this problem right.... as i have not used either of the bits of given information about p = 1 and at what lengths the resonance occurs at :S well anyway, heres my answer, what do you think?

lol so the radius of convergence is 3/2 ?? i am getting a bit confuzzled here

oh i think i've got one.... how bout this series for b(n): ...series or should i say sequence...i am not sure

hmmm ok, your right (yet again! ), would you be able to give me some help with the second part of the question (...finding the example)

nevermind, sorry, please ignore this thread

oh ok , well i'll try again later and show you, thanks though

i am not sure this is true... (i'm probably wrong, so correct if i am ) well what if the sum just goes from n = 1 to 1 ?? then it would be <= wouldn't it? or ....not?

oh wait well i got the proof right but i still don't know what an example would be...hmmm

v1 and v2 are vectors from V and u and w are vectors in the subspaces U and W respectively or i suppose you could just call u and w the zero vector for each subspace (but since they are subspaces it is the same zero vector in both of the subspaces and the vector space V)

thanks for you help everyone!

haha yes anyways... well what about for part a) how do you think my answer for that looks?

oh and for part b) i would say something like A = [a] [0] B= [0] [c] [d] and the interesection of these two planes is a line along the y-axis what do people reckon?

ok i've got a proof.... what do you guys think?

hi, yet another one of my questions i can't quite figure out how to prove this....i can see its true, but i just don't know how to write it out formally :S -Sez

oh ok, lol, i havent yet done the binomial expansion, so yeah didnt know that! thanks DQW!

oh ok i see, well thanks again DQW yay! i actually got a proof right! (well 90% right anyways )

well when i say "made it up" i ment i sorta tryed a few cases, and saw that it worked, so then assumed it worked for all cases (quite dodgey i know). would you be able to point me to somewhere where i can find this inequality written out properly (i.e. a maths webpage or something?) also i am gathering if that ineqaulity holds, then the rest of the proof is correct? Thanks for the reply DQW:)

hey i am not sure whether i am getting this problem correct... i reckon the answer would be: f(n) = nv/{lamda1} ; where n = 1, 3, 5, 7, . . . {lamda1} being the fundamental harmonic's wavelength, and v being the speed of sound in air well anyway, thats what i think the answer is but yeah i am new to thise stuff, so just thought i'd check -Sarah

ok yep sorry i goofed yeah i get 3/2 aswell thanks dave!