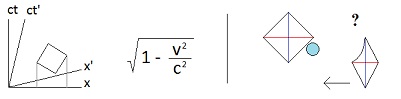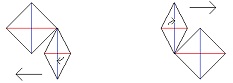Thales et al

https://www.youtube.com/watch?v=tJ2AJJMcQXs I was watching this lecture by a MIT professor, and something didn’t seem quite right to me. Perhaps someone here can set me straight. If a light source and an observer are moving away from one another, the flash of light will be redshifted. If the light source is considered to be in motion and the observer is considered to be at rest, or if the observer is considered to be in motion and the light source is considered to be at rest, either way, the same redshift logically occurs. Conceptionally, it’s either drawn out as it leaves the light source or its drawn out as it’s being perceived. He then goes on to say that if the observer is considered to be in motion, and so the time dilation is with the observer from the perspective of the light source at rest, that this will also contribute to a redshift. That doesn’t seem right to me. From the perspective of the light source at rest and the observer in motion, with the observer’s time slowed down, that seems like it should contribute to a blue shift. Right? If the observer’s time slows down, then the oncoming wave, for the observer, should be oncoming faster, based on the moving observer’s slower time. If the observer is considered to be in motion, then it seem like the flash of light should tend to be redshifted based on the relative motion but also oppositely tend to be blue shifted based on time dilation. No?

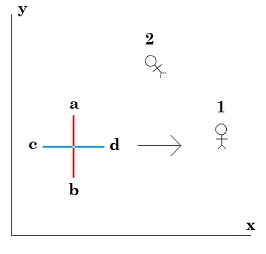
Yep. I get it. Thank you. I felt comfortable that I had resolved the two colliding diamonds, and there was no paradox, but you resolved it better. My analysis was not right. The problem I’m having is how to resolve this when a third body (such as a water balloon) is added. Whether the water balloon is large and it collides with the second diamond first, or whether the water balloon is small and the diamonds collide first, doesn’t matter. I’m having the same problem in either case. Starting with your analysis of the diamonds colliding first, it still appears to me, that if there is a third body (such as a water balloon) between the two colliding walls, that in the inertial frame of reference of the upper diamond at rest the balloon will be pushed down and to the left. While in the inertial frame of reference of the lower diamond at rest, the water balloon will be pushed up and to the right. ? Say there is an X moving in inertial frame of reference xy in direction 1. And say there are two people (observer 1 and observer 2) at rest in xy. From the perspective of observer 1, arm ab is perpendicular to the direction of the motion and is not length contracted, and arm cd is in line with the direction of the motion and so is length contracted. Observer 2 is in the same position as the diamond at rest in thought experiment presented above. Are you saying that for observer 2, who is in the same inertial frame of reference as observer 1, the X is somehow length contracted differently than it is for observer 1? (And, if so, are you saying this is physically true and not just a matter of appearances?) I think in the end, when the diamonds are spinning around clockwise with one another, they are in the same frame of reference. But I think at the moment of impact they are necessarily in two different inertial frames of reference. No? The water balloon, like and even more so than the diamonds, is not a perfectly rigid body. When you fall fast into a pool of water, it hurts like hitting a solid, but the water does move. When the water balloon collides with the second diamond, and is then squeezed between them, it will not act like a rigid body. It will be squeezed and distorted and move. Or, so I think. (For the purposes of this thought experiment, we can stipulate an unbreakable rubber balloon.)

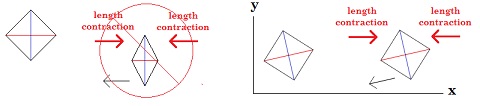
If length contraction of the moving diamond occurs in the direction of its motion, then, yes, its length contracted walls remain straight lines. (If a square is length contracted in the direction of its motion, then it’s walls too remain straight lines. If a circle is length contracted in the direction of its motion, then, somewhat differently, its circular shape becomes an oval.) And so, yes, I am assuming straight lines. If I’m wrong in this, please let me know. Is there a way for the moving diamond to length contract so that its walls are not straight but curved? If so, then if curved in just the right way, then this could lead to the colliding walls of the two diamonds being parallel to one another at the point of impact with the balloon. And so, this could then lead to a solution to this “paradox.” But I can’t see it. If a moving body is not only length contracted in the direction of its motion but it is also tilted, and if a moving body is not only titled but curved, then if curved in just the right way, then this could lead to the colliding walls of the two diamonds being parallel to one another at the point of impact with the balloon. And so, again, this could then possibly lead to a solution to this “paradox.” However, I have not found any support for this in either the “Bar and Ring Paradox” or in “Terrell Rotation.” If my understanding of these is correct, there is a “tilting” or a “rotating” but not a “bending.” And, further, while the Bar and Ring Paradox suggests an actual physical tilting, if I’m reading the Terrell Rotation Wikipedia link correctly, this refers to appearances and not the actual physical contracted configurations. And of course to resolve the “paradox” here with the balloon, the moving diamond would actually have to be physically tilted and/or bent for the walls of the two colliding diamonds to be parallel at the point of impact with the balloon. ?

The way I set up the thought experiment the balloon is in one or the other of the two diamonds inertial frames of reference. It could be either one. In the drawings I have the balloon in the upper diamond’s inertial frame of reference. And so, to answer your question, in the balloon’s initial inertial frame of reference, it ends up moving down and to the left. (Once the balloon squeezed it is then in motion in all different kinds of directions and is no longer “inertial.”) (And if the balloon where initially in the lower diamond’s inertial frame of reference, it would then end up moving up and to the right.) Did I answer your question? In a nonrelativistic world, from the perspective of the lower diamond at rest, the colliding walls of the two diamonds remain parallel, and so the balloon, in the end, has no tendency to move up or down. And, from the perspective of the upper diamond at rest, the colliding walls of the two diamonds also remain parallel, and so the balloon, in the end, has no tendency to move up or down. And so there is no paradox. Here, in a relativistic world, to also end up without a paradox, the balloon, in the end, must do the same thing in both frames of reference. I can’t see a way how it would move up in both or down in both. The only possibility I can see is that the balloon must remain in place in both. And the only way I can see it remaining in place in both is if the walls of the two diamonds are parallel at the time of impact. If the walls are not parallel to one another, then the balloon will be squeezed in one direction or another. I thought this must be the solution: in addition to being length contracted, the moving body is also rotated relative to the body at rest. And I found support for this idea in the “Bar and Ring Paradox.” (https://en.wikipedia.org/wiki/Ladder_paradox#Bar_and_ring_paradox) The problem with this is what happens if you have two sets of two relatively moving bodies. If I’m right (… if, if, if …) and the only way to get the same result in the end is for the balloon to remain in place in both inertial frames of reference. And if I’m right (… if, if, if …) and the only way for the balloon to remain in place in both inertial frames of reference is for the colliding walls to be parallel to one another. And if this is achieved by the moving bodies not only being length contracted but also tilted, then both of the two bodies in each inertial frame of reference must be tilted when considered to be the bodies in motion. But this leads to a problem. (And I ran into the same problem in the “Bar and Ring Paradox” if its extended to include two bars and two rings.) If the two bodies are connected, then in the inertial frame of reference of them at rest, they remain connected, while in the inertial frame reference of them in motion (where they are tilted) they cannot remain connected. And so, by resolving the initial “diamond paradox” with “relativistic titling,” I found myself ending up in a second and different paradox. Maybe someone else here in this forum can see what I can’t see, and tilting can actually work. Thank you for the Terrell rotation link. I think “relativistic rotation” would end up in this same secondary paradox. No? Something I can’t see? What do you think? Thank you for the center-of-mass/energy link. “Recall that this is the speed in the center of mass frame, and for practical purposes, like designing the accelerator, we need to know the energy necessary in the “lab” frame—that in which one of the protons is initially at rest.” I read through it a few times, but I couldn’t find a solution here from that. Maybe there is something that I missed. Let me know. I googled “length contraction” and “line of sight” but I couldn’t really understand it. Are you saying that a body in motion does not length contract in the direction of its motion in the other body’s inertial frame of reference at rest, but rather it length contracts in its direction of motion relative to the other body itself at rest? And so, I was wrong in my thought experiment to suppose that the moving diamond will be length contracted as shown on the left, but rather it will length contract along the x axis relative to the body at rest, as shown on the right, in its horizontal motion relative to the body at rest and not in the direction of its actual motion in the entire inertial frame of reference of the body at rest? Do I understand you correctly? No? Right. I glossed over the non-rigid aspects of the solid diamond shaped bodies. In the first example, no balloon, when the leading edge of the diamond at rest collides with the edge of the length contracted diamond in motion (in both frames of reference) the diamond at rest will contract from the collision and the diamond at rest will begin to accelerate due to the collision. This contraction and acceleration will take some time (at the speed of light or less) to makes its way through the entire body of the diamond. And when the two diamonds collide, the diamond in motion (in both frames of reference) will start to expand (except for at its very tip), and the diamond in motion will start to rotate, and the diamond in motion will start to decelerate. This expansion and rotation and deceleration will take some time (at the speed of light or less) to make its way through the entire body of the diamond. In the second example, the one with the balloon, at one point I thought I had found the solution to this “paradox” with this concept of “no body is a perfectly rigid body.” After the balloon collides with the second diamond, and it is in contact with the two closing in diamonds, this impact and pressure not only distorts and squeezes the balloon, it also distorts the more rigid, though not perfectly rigid, diamonds. And, I thought, if this could lead to the walls of the diamonds being distorted into being parallel, just after the impact, then this could possibly lead to the solution. This could mean that the balloon remains in place. And so no paradox between inertial frames reference. There are three problems I came up against in this line of thought. First, when the impact between the balloon and the second diamond distorts the length contracted diamond and when the impact between the balloon and the second diamond distorts the diamond at rest (no matter if the balloon is in one inertial frame of reference or the other), the distortions will likely be in the opposite direction needed for the walls to become parallel. Second, while the distortion from the contraction of the diamond at rest the distortion from the expansion of the diamond in motion do occur in the directions needed to make the walls parallel, by the time this happens (first the ends of the diamonds must collide), the balloon in the two different inertial frames of reference has already been squeezed differently and in two different directions. And, third, while the diamonds will contract, and while this will have an effect on the squeeze of the balloon and therefore its resultant motion, these contractions of the diamonds will then become expansions, as the diamonds reassert their shapes after the impact. And this contraction and expansion will occur at something less than the speed of light across their bodies and then back, but it should occur at a must faster rate than the actual squeezing out of the balloon from between them, and so may be of no impact in the end. Well, that’s where I ended up. Let me know what you think.

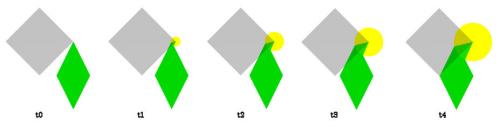
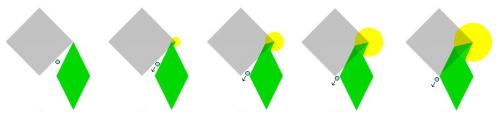
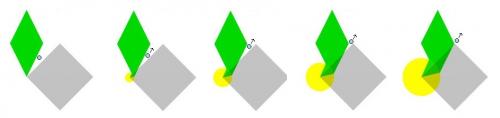
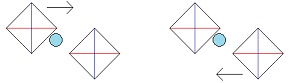
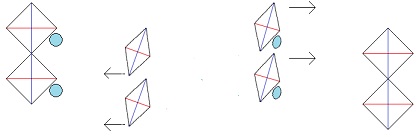
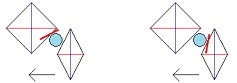
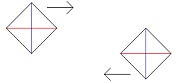
Two diamond shaped bodies are moving towards one another. The lower right side of one is aligned with the upper left side of the other. In a relativistic world, in the inertial frame of reference of the upper diamond at rest, the lower moving diamond is length contracted in the direction of its motion. And, in the inertial frame of reference of the lower diamond at rest, the upper moving diamond is length contracted in the direction of its motion. In the inertial frame of reference of the upper diamond at rest, the leading edge of the upper diamond and the upper edge of the lower diamond collide first. And, in the inertial frame of reference of the lower diamond at rest, the lower edge of the upper diamond and the leading edge of the lower diamond collide first. This means, in the inertial frame of reference of the upper diamond at rest, after the initial collision the lower diamond rotates clockwise, and, in the inertial frame of reference of the lower diamond at rest, after the initial collision the upper diamond rotates clockwise. (Once they begin to rotate they are no longer “inertial frames of reference.”) This is not a paradox. In a relativistic world the sequence of events in one inertial frame of reference can be the inverse of the sequence of those same events in another frame of reference. And here, in both frames of reference, once the length contracted diamond rotates and expands and collides fully with the other diamond, the other diamond will also be set in clockwise motion. And so, from the perspective of both frames of reference, in the end both diamonds will be in clockwise rotation. It’s just the sequence of events that differs. There is now a water balloon next to one of the diamonds and along the wall that will collide with the other diamond. It is in the same inertial frame of reference as the diamond it is next to but it is not attached to that diamond. When at rest it is round in shape, and so when in motion it is length contracted into an oval. The water balloon is large enough so that before the two diamonds collide with each other, it collides with the other diamond first. It is then squeezed in between the walls of the two diamonds as they close in on one another. In a nonrelativistic world the walls of the two non-length contracted diamonds would be parallel to each other and so the balloon would have no pressure to move in one direction or another. However, here in a relativistic world, in the inertial frame of reference of the upper diamond at rest, the water balloon is squeezed down and to the left, and in the inertial frame of reference of the lower diamond at rest, the water balloon is squeezed up and to the right. In one inertial frame of reference the water balloon will move in one direction and in the other inertial frame of reference the water balloon will move in the opposite direction. This is a paradox. What is the solution?