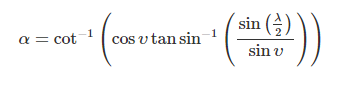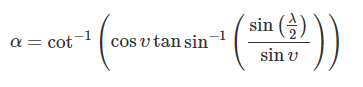steveupson

Well, until you do the math these questions will remain unanswered for you. The math is the answer to these questions. Do the math. I'll try to walk you through it. Can you define alpha, lambda, and upsilon yet?

Yes, and also down. Although they are independent from one another, they are all in the same geometric frame. Actually, I think that this is always generally true in projective space. In Euclidean space we can have unique planes that don't intersect if they are parallel, but if that were the case then they would share the same surface normal, wouldn't they? Or would we say that the origin of the normal vector must also be specified? Either way is fine, but we need the specificity. The math doesn't define an "absolute up" or a "universal up." The math only shows that they must both exist, and that they are one and the same thing. We can set the math to the side for a moment and try to understand how directions are organized in nature. There, everything is organized into a coherent mess by time. So, we really have two different ways to look at space as a general proposition. We have the mathematical description (which is an abstraction comprising symbols) and then we have the actual stuff that the universe contains. If we make the assumption that everything is in motion, then each thing has its unique direction in which it moves (with the exception of entangled pairs.) Since we understand time and space to be intertwined, and that we can call positions in spacetime events, and since time "moves" or "changes" in a specific way, then we can make the supposition that everything moves or changes in a specific direction (toward the future), even if the actual position in space does not change or move. Everything has a future that lies is a particular direction. All these directions are related to one another by the math. Yes, of course. Your username?

I think that you're correct with the definitions. The fact that you made reference to surface normals simplifies things tremendously. The surface normal represents a direction in space, which can be up, down, or off-to-the-side. We could also specify this particular direction by specifying the plane that the surface normal is normal to. The plane and the normal both specify the exact same direction in space. This is important to understanding how the geometry works, mathematically. We can have three directions in space, call them alpha, lambda, and upsilon, where no two of these directions are the same. We can specify these three directions by either defining the plane or the vector that is normal to it. Specifying the plane allows certain calculations to be performed that will produce a mathematical relationship between the three unique planes. Note that since they are each unique, they must have a single intersection in space. That's the beginning of how to do the math. One more thing that should be understood from the start is that this particular geometric relationship between these three unique directions has never even been hinted at before, except perhaps by Hermann Grassmann in these translated quotes: What he is referring to is what we believe to be the specific mathematical relationship that we're now using for timespace based on what we're calling synchronous geometry. We have derived a "tridentity" that expresses a direction in space, and it does it by a fundamentally different means than how it is normally accomplished using today's methods (today's methods being to define vectors in a plane or surface.) Modern methods seem to be completely unaware that there is a difference between how these angles interact in space and how they interact in a plane. There is a .pdf file that explains the derivation of the basic formula: tridentity review copy.pdf The .pdf file does need peer review if anyone is interested in making contributions. I'll try to answer any and all questions, although there may be some delay in my ability to respond to specific members. I'll try to keep up with what's going on in this thread.

The experiments that proved there to be no luminiferous aether did NOT prove that there is no "universal up" or "universal down." Universally, up is always away from a gravitational well and down is always toward it. This isn't the same thing as there being an "absolute up" or an "absolute down." Or is it the same thing? Can anyone explain why these two things would be different? Use your math and explain. I can explain how they are the same. Using my math.

It's the same subject. I can, and have, shown this mathematically. If we're defining the "thing" as what Mach and Dirac and Grassmann and Einstein were referring to, then we are talking about the same exact thing. Do the math.

So, conclusions about ether would be off-topic in this thread. I don't think that you're joking, either.

Which conclusions do you mean? I think that you're being genuine, but I could (and have) made the same argument about direction. The terminology is applied to many different concepts. There's the way that we represent direction mathematically in physics, and then there's the actual stuff that exists out there in nature. Space is the same thing. There's the actual stuff that exists in nature, and then there is our mathematical description of that stuff. I'm not sure why this is disputed or considered to be some kind of "pet theory." The lack of specificity is a real problem, and can lead to semantic disagreements that don't really speak to the underlying scientific facts. I prefer to couch these discussions in the math. If you are unwilling or unable to do the math then it becomes very difficult to explain the mathematical conclusions. Without doing the math it is easy, way too easy, to just shrug things off as unfounded baseless nonsense. The mathematical relationships are not nonsense, they're math. They are either correct or they are incorrect. It has nothing at all to do with anyone's background or training or perceived abilities. You've followed this project for years. You've seen with your own eyes how this function (that isn't a function) was derived. It's one thing to be constantly proven wrong, and it's a completely different thing to be constantly proven right. If I'm wrong, prove it. Iv'e provided what should be adequate proof that I'm right about most of this. At the very least the topic of the mathematics, and how they relate to physics, should be allowed to be open for discussion here. That's all that I've ever asked.

Do you mean this? It's trigonometry. You know, geometry? What's unfounded baseless nonsense about mathematics? Then I apologize for the accusation, if that wasn't your intent.

I think that some people really resent the fact that they don't know certain stuff. It's as though they try to cover their resentment with all sorts of recriminations, some of which are extremely dishonest. Take for example a member who asks, seemingly innocently, "are you talking about the luminiferous aether?" which when you think about it is the same as asking "are you a "flat-earther?" The question seems innocent enough, but it isn't an honest question. It isn't as if the questioner is unable to discern the answer. This "behavior" is what should be looked at an rooted out by enforcing a common code of decency on fora like this. No one deserves to be treated this way, with such arrogant disrespect. And yet this is the type of behavior that is encouraged here. I don't understand why people choose to act this way either, and I really don't understand why it's allowed. And if anyone were to ever complain about such a thing, by golly they most likely will be permanently dismissed without any further retrospection. Oh well, we'll see. Mathematics is not some pet theory of mine.

This is an incredible discussion. It's a shame that this topic is forbidden for some members.

At the Planck scale, direction and distance don't have the same relationship with one another as what they have at the human scale or astronomical scale. Think about a car that needs a certain width of road in order to make a u-turn. When the road narrows to below the Planck length it is no longer possible for the car to drive in a circle. It is very likely that a turn in space occupies some amount of direction that cannot be made into a different, smaller amount. This could be caused by the necessity that the turn in space has to be relative to something. I won't say it's an aether, because admitting to a belief in an aether is right up there with denying that you're an alcoholic (denial is the first sign, by the way, and that's why we should never deny it.) Mach's principle may be in play here. It does look as if there is some room here in this particular model for some discrete math.

I’ve wanted to reply to several of the ongoing discussions here, but I’ve been a little overwhelmed by events. (For one thing, I’m going to school again, and I’m trying to study algebra – I’m still no good at it, but I think that I’m learning exactly why I suck at it so bad.) I’ve also taken an interest in this question recently, and it seems to me as if our mathematics have always been developed in response to questions raised by observations of physical phenomena. Newton’s calculus used for explaining his laws of motion would probably be the most obvious example of this. For those more critical members here that may be offended by me “reintroducing” my opinion at this forum, please do take a look at the interactive video on quaternions that is linked at the end of this post. It seems to be transformative for this type of learning. Also, Cohl Furey from the first link in the OP has an interesting set of more traditional video lectures that concludes with octonions. There’s a fairly recent paper (2015) where the author explains more of the history of how we got here. It reaches back to Grassmann’s time, and it sort of charts the path that was developed for transitioning between what used to be an understanding of Euclidean 3-space based on spherical trigonometry, and the modern version that is mostly based on vector manipulation (as expressed in the Cartesian coordinate system and some of the higher-dimensional geometries) that is currently popular in physics. The paper is “QUATERNIONS: A HISTORY OF COMPLEX NONCOMMUTATIVE ROTATION GROUPS IN THEORETICAL PHYSICS by Johannes C. Familton” and can be viewed here: https://arxiv.org/ftp/arxiv/papers/1504/1504.04885.pdf It’s a pretty long read, so I’ll try and condense the parts that were the most important for me. My understanding of how this all fits together is still being improved, but I was drawn to the parts in the paper where certain persons spoke about the conceptual (or mathematical) distinction between scalars and vectors. Here are just a few examples of what I’m talking about: As many of you are aware, we (a loosely affiliated group of volunteers) are currently working to develop a new geometry based on newly discovered geometric relationships. In all of my attempts to explain the math that underlies this new geometry, most of the difficulty is over this specific issue. We've never really developed a fully comprehensive understanding of how these two types of numbers differ, and this has led to a very imprecise way of speaking about those differences. In my opinion, the most accurate way to define the difference between these two types of numbers is to recognize that one type of number is a ratio, and the other type of number is a quantity. We’ve sort of muddled this all together into pabulum like “a vector has magnitude and direction while a scalar has only magnitude.” Although this may be true, it leads to a very anemic understanding of what’s going on mathematically. Grassmann seems to be the first to understand that there is a mathematical difference between things that have a direction and things that don’t, and to try and make a study of it in a way that produced results that are still in use today. Our new understanding (in our informal group) is that there are two distinctly different quantities that make up space or volume. These two quantities are distance and direction. We think that we have developed some math that shows how these two quantities are NOT asymmetrically inseparable from one another. What this last statement means is simple and intuitive, but it also “seems” as if it is in direct conflict with millennia of accepted math and science. In actuality, there isn’t really any conflict at all, the old and the new fit together perfectly. What is new is that we can now talk about the direction part of the “vector” separately, in the same way as we have always talked about the scalar portion as being separable. We can assign a meaningful number to express direction as a quantity, instead of as a ratio. When we do this correctly, we should be able to express distance as a ratio between directions. This is a perfect symmetry to the way that we now treat direction as a ratio between distances. We're catching spherical trigonometry up to include 21st century observations in physics. All mathematical inquiry into this subject ended fairly abruptly a century and a half ago when quaternions and vector analysis became all the rage. There are some geometric relationships that are not captured using these traditional methods. We have stumbled across some of them and we are attempting to use them in order to define a geometry that is different. While the observation of physical phenomena remains identical, they can be looked at using different mathematical models. It's the same as reading Don Quixote in two different languages. For more about quaternions, check out: https://eater.net/quaternions

How do you carry position information except for in spacetime? Granted, we can remove the base quantity of time from the information and we have position in space, which is only a partial description of position. Similar constructs can be made using any of the other base quantities, such as mass, temperature, luminous intensity, or amount of substance. Another example would be the information contained in the expression of density. If we remove either component (volume or mass) we no longer have density information. The ratio between volume and mass "carries" the density information.

Each frame in spacetime has a now that can be temporally separated mathematically. By absolute I mean mathematically unique. The frames themselves remain relative to one another (observer dependent) and so are not universal. Information carried by spacetime is position. I imagine that I have a different way of viewing these things. Information, to me, is any derived quantity. Volume is derived from length. I'm, like you, not onboard with an argument that length is a physical quantity but volume is not. Once any derived quantity is reduced to a base quantity (mathematically) then any information is lost. There's nothing to relate it to.

I'm fairly confident that the math shows the existence of an absolute now, which isn't universal and which differs mathematically from the past or future. Interestingly, these same mathematical necessities are responsible for the understanding that there is no absolute direction but there does exist a universal direction (established by the arrow of time.)

How do we consider simultaneity in a non inertial frame?

What is the definition of ether? Which one are we using in this discussion? The most childish definition is "a proposed medium for the transmission of light." Are we forced to converse like children and use this definition? Of course not. How about something along the lines of Mach's Principle or "In later years there have been a few individuals who advocated a neo-Lorentzian approach to physics, which is Lorentzian in the sense of positing an absolute true state of rest that is undetectable and which plays no role in the predictions of the theory. (No violations of Lorentz covariance have ever been detected, despite strenuous efforts.) Hence these theories resemble the 19th century aether theories in name only. For example, the founder of quantum field theory, Paul Dirac, stated in 1951 in an article in Nature, titled "Is there an Aether?" that "we are rather forced to have an aether".[10][A 20]However, Dirac never formulated a complete theory, and so his speculations found no acceptance by the scientific community." https://en.wikipedia.org/wiki/Luminiferous_aether#Other_models Gee, what could satisfy these requirements? I wonder..

got that right

Ok then, what is the definition? This discussion is about science. Why do y'all insist on making it about me? It isn't my fault that the universe is the way it is.

Of course, Mach and Gödel would be banished from this place under these conditions. There is that, too.

It's not guesswork to say that, in general, the "theory of ether" is undefined. Newton's bucket argument probably best identifies the requirement for an "ether." The quantity that we refer to as direction does meet this requirement.

Base quantities are what are used to form other quantities, or derived quantities. This is a common mistake, one that I myself have made. A ball is a 3D object. A sphere, by definition, is a 2D surface. It's an abstraction; a mathematical object perhaps - definitely not a physical object.

This is an important point and it isn’t just a semantic argument. I hope this can be discussed without sounding condescending, which isn’t the intention. The intent is to try and highlight a potential problem with the jargon that is being used. Back when our discussions of direction first began, it was asserted that the term direction had a very specific meaning with regards to mathematics. Direction is something that is expressed by a vector. No one has any argument with that. I then suggested that perhaps the term orientation could be used in order to distinguish this component of a vector from all of the other types of direction where a vector isn’t possible. In other words, we needed a term that could be used to express this property, quantity, attribute, parameter, or whatever (no one seems to know exactly what it is, except that they somehow know or intuit without any published mainstream science that it isn’t a base quantity), in those cases where a vector doesn’t exist. Using only the radius of a sphere we can know the diameter. The orientation or direction of the diameter isn’t necessarily known. At the same time, the idea that it has a direction cannot be ignored. Its direction lies between two antipodal points. Its direction is such that it passes through the sphere center. We know these things are true about the direction of the diameter without being able to specify the direction. Therefore, it must have a direction, even though it isn’t specifically specified. Your Legendre polynomials are no different than this example for the diameter of a sphere. Even though the actual value is unknown, we do know that the direction is axiomatically limited by the definition (words like azimuth and Euclidean length) in the same way as a diameter has a direction that is also limited by the definition.

Time is a base quantity. Orthogonal is an orientation.

It's very similar to the hairy ball theorem. Most reference frames are oriented to each other in an organised fashion, like the combed portion of the hairy ball. The math indicates that there are a class of frames that can be chosen that are not directionally related to the organised ones. In other words, there actually is a mathematical distinction that can be shown between what we call now and what we call the past or future. This is another fundamental part of the theory. All directions commute mathematically in the now frame and they don't in the past or future frame. It's more complicated than that because every frame in the past and future does have one instance where a direction does commute, but then all of the rest do not ( at least until we reach the Planck scale.) on edit>>> There is some literature on the mathematics involved using a different approach. It is the same thing that causes the failure of the Whitney trick in dimension 4: https://en.wikipedia.org/wiki/4-manifold#Failure_of_the_Whitney_trick_in_dimension_4