-
Posts
296 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by steveupson
-

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
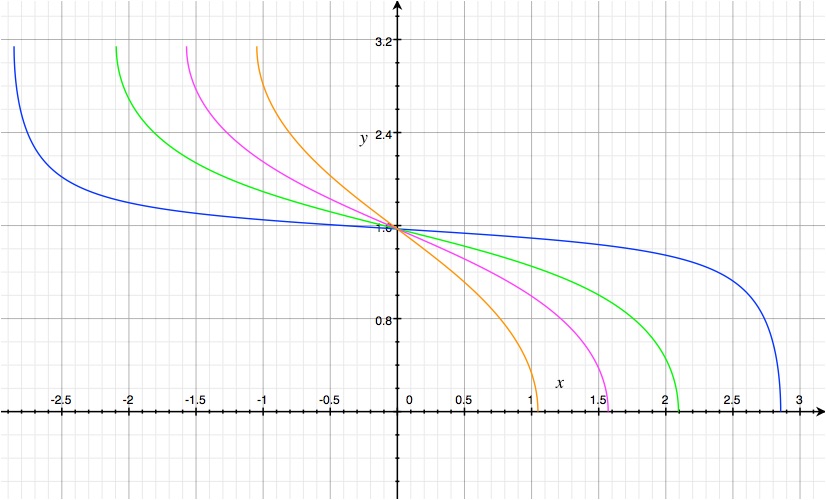
Calculus has no impact on this issue. It's strictly plane and spherical trigonometry. Believe me, if calculus were required then there would be calculus in the equations. The quantity of direction is something that you yourself have graphed on different occasions, although you remain unaware of the significance of those graphs. The area under each 2D curve for different upsilon angles is a quantity that expresses the amount of direction that angle possesses in 3D space. It is impossible to understand these words until the math is properly understood. For a sine curve (which occurs with [latex]\upsilon=\frac{\pi}{2}[/latex]) the quantity is [latex]\frac{\sqrt 2}{2}[/latex]. When the curves are "normalized" in order to eliminate the length differences associated with the radius of the small circle compared to the radius of the sphere (similar to the way standard vectors are normalized in order to generate direction vectors), then the area under each unique curve is properly scaled to represent the unique 2D quantity that represents that portion of a 3D turn. This particular 2D (graphical) representation of the 3D direction (or angle or orientation) is very different from what we are used to in that it represents the mathematical quantity or magnitude that is associated with each change of direction in normal space. It is mathematically a quantity or a scalar, and it can also be thought of that way in order to better understand the relationships that exist. Yes, surfaces are two-dimensional objects. The methods that we generally use in order to specify and manipulate the mathematical representation of direction in these two dimensional objects are called plane trigonometry. There is another type of trigometry that isn't plane geometry, called spherical trigonomety and it is used in order to examine triangles on a sphere or ball, or in other words it can be used to establish geometric relationship in either two or three dimensions. We're concerned with the interplay between these. Normally, the sphere and ball have the same trigonometric identities. They are actually very different mathematically or geometrically. The ball has a center which makes it a three-dimensional object. Therefore there are three-dimensional identities associated with it that cannot be associated with a sphere. Returning to this issue for a minute, maybe someone who knows more about this stuff than I do can explain something to me. We have [latex]\sin{\upsilon}= \frac{\sin\frac{\lambda}{2}}{\cos\frac{\phi}{2}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\:\:\:\:(4)[/latex] and [latex]\cos{\upsilon}= \frac{\cot\alpha}{\cot\frac{\phi}{2}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\:\:\:\:(5)[/latex] and since, [latex]\sin^2 \upsilon+\cos^2\upsilon=1[/latex] then we should get a new spherical trigonometry identity: [latex](\cos\frac{\phi}{2}\,\sin\frac{\lambda}{2})^2 +(\cot\frac{\phi}{2}\,\cos\alpha)^2=1\quad\quad\:\:\:(6)[/latex] Why isn't this all true? Did we break trigonometry or did we break algebra? What's up with this? Anyone? -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
Of course direction is represented the same way in 2D and 3D. That's the whole issue. That's why it's important to look at the mathematics that underlie that treatment. It isn't me who says nonsensical things, it's the numbers, the math, the geometry. A turn in three dimensions is mathematically different than a turn in two dimensions. That's not me saying it. That's what the math proves. That's how you can have an identity that occurs in three dimensions that doesn't occur in two dimensions. I'm not making any of this up. It's the way the universe is built. And it makes absolutely no difference at all until you try and model spacetime because space with direction as a scalar value reacts differently with time than space with direction as a vector. You must know that scalars and vectors are mathematically different. -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
There may be no way for the math to make sense to you. It will probably make more sense when it's more fully developed and discussed. Many members at many fora have made discussion of the math almost impossible, which is a shame. -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
I don't know of any simple way to go about this explanation except with the mathematical truths. Every time I try to put context to the math I am called a crackpot. Let me try one more time. In 2D direction is always a vector or ratio quantity. In 3D direction is always a scalar or magnitude quantity. Sometimes the two quantities for expressing direction are the same, but most of the time they aren't. In curved spacetime this mathematical reality causes issues with how the equations commute . It appears that there is only one instance in any reference frame where the the two are the same, or where time and space commute (where the distance and direction from event A to event B is the same as the distance and direction from B to A.) The tridentity identifies the difference between these two sets of relationships or orientations, the ones that can only exist in 3-space and the the ones that can exist in both 2-space and in 3-space. A mathematical definition of a turn in 3-space is a different mathematical thing than the definition of a turn in a plane. The reason that they are different is because of the relationships that are identified by the tridentity. So, was that a yes or a no? I'd be extremely interested if there are any spacetime models that are not non-Euclidean. -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
Are there any spacetime models that are not non-Euclidean? -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
These scalar values are directions. They have no length component. Therefore, direction is a quantity. -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
second edit: tridenty? third edit>>> I need to correct the first edit. What we have in 3-space are the three points a,b,c and the origin of the Cartesian coordinate system. These points also make angles with the origin. When all of these angles can be projected into 2D without change, then the identity does not exist. This is what distinguishes 2D geometric functions or rules (Pythagoras, pi, trig) from the 3D functions or rules. All of the 2D functions and rules are applicable to 3D, plus and entire new set of new functions and rules. The reason we never knew about them is probably because we always just reapply the 2D rules over and over again thinking that this is sufficient. It isn't enough; there's a lot more to 3-space. -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
The identity is important because it defines which particular aspects of Euclidean 3-space are currently being ignored in our mathematical models of spacetime. The stuff that the equation shows to be an identity in 3D is the stuff that is not currently being captured in our relativistic transformations. The stuff that the equation includes that is not an identity is the only stuff that is being included in our spacetime models. In other words, our spacetime models only represent the mathematical relationships that occur in the instances of geometric descriptions that are like the one that you gave. Our spacetime models do not represent the rest of the plethora of additional geometric relationships that are present in Euclidean 3-space. We appear to be ignoring what Euclidean 3-space actually is when we go about trying to bend it. We should apply this new information to the model before we try to come up with relativistic transformations or they will never be very accurate. One more time; how can we mathematically represent the effects of gravity on spacetime when we are not using an accurate model of space? The projection is 2D vs 3D representation of the values. I don't understand your question. edited to add: We have three points a,b,c in space. There are three angles that can be formed using these points as vertices, abc, bca, cab with values x,y,z. If these thee angles in space can be parallel projected onto a plane where x=x’, y=y’, z=z’ then we have a case where the values (identical values) exist in 2D and 3D. In this case there is not an identity. In every other case there is. I don’t know the word for this. I’m quite sure that there is no word for this. The lack of proper nomenclature is another issue, in addition to the math. second edit: tridenty? -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
First, I want to thank you folks for taking time to look at the math. I know that it doesn’t seem worth your while, but if we can talk more about the math then we can probably begin to make some real progress. A projection from 3D to 2D is commonly described as taking a wire frame of the 3D object and placing it on a piece of paper that has been laid on a table. Light passing through the wire frame will cast a shadow on the paper, and depending on where the light source is oriented in relation to the object there can be different results, or different shadows cast. When the light source is directly above the object and the rays of light are parallel, this projection is often called an oblique projection. If we take the example that was given in your post and project it onto a 2D plane then the projection contains the identical values as the 3D object. This is because the values that were chosen are for an instance where the small circle is at maximum (has become a great circle) and this causes all of the angles in the model to collapse into a 2D construction. In other words, the expression is expressing a relationship that exists in 2D and the expression is not an identity in 2D. For some further illumination, it is possible for the function to go beyond a great circle, but when this occurs it actually becomes a small circle on the back side of the sphere. This issue can probably dealt with mathematically with the use of imaginary numbers. The use of imaginary numbers to describe this part of the function was first discussed publicly back in July of last year I only mention this in order to show anyone who thinks I’m making this all up in order to engage in some tit-for-tat rhetorical argument that this is not the case. The math is the math. It’s what it is. And it isn’t my fault that it is what it is, either. Our research has progressed a great deal since then, but we are coming to a big slow down in our efforts because we need help with the math. Understand that our research is way ahead of where the math currently is. We need to get the math caught up with where we’re at. -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
How did that extra + sign get there? [latex](\cos\frac{\phi}{2}\:\sin\frac{\lambda}{2})^2 +(\cot\frac{\phi}{2}\cos\alpha)^2=1\quad\quad\:\:\:(6)[/latex] sorry people, I want to say that it wasn't my fault- 93 replies
-
-1
-

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
The answer to the previous question might be contained in the methods that were used in order to solve for the underlying function. The model was solved for a family of functions with a fourth variable [latex]\upsilon[/latex]. In order to compose the function [latex]\alpha=f(\lambda)[/latex], this fourth variable was held constant. The process for coming up with the identity was this: analysis of the geometric model gives two simultaneous equations: [latex]\cot\alpha = \cos\upsilon\tan\frac{\phi}{2 }\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\:(1)[/latex] [latex]\sin\frac{\lambda}{2 } = \sin\frac{\phi}{2 }\sin{\upsilon}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\:\:\:(2)[/latex] The function [latex]\alpha=f(\lambda)[/latex] is: [latex]\alpha={\cot}^{-1 }(\cos\upsilon\tan{\sin}^{-1}(\frac{\sin\frac{\lambda}{ 2}}{ \sin\upsilon}))\quad\quad\quad\quad\:\:(3)[/latex] It is a smooth function that approaches a sine curve when [latex]\upsilon\to0[/latex], and that approaches a hyperbola when [latex]\upsilon\to\frac{\pi}{2}[/latex]. Equations (1) and (2) can be rewritten in the form of: [latex]\sin{\upsilon}= \frac{\sin\frac{\lambda}{2}}{\cos\frac{\phi}{2}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\:\:\:\:(4)[/latex] [latex]\cos{\upsilon}= \frac{\cot\alpha}{\cot\frac{\phi}{2}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\:\:\:\:(5)[/latex] and since, [latex]\sin^2 \upsilon+\cos^2\upsilon=1[/latex] then we should get a new spherical trigonometry identity: [latex](\cos\frac{\phi}{2}\:\sin\frac{\lambda}{2})^2 +(\cot\frac{\phi}{2}+\cos\alpha)^2=1\quad\quad\:\:\:(6)[/latex] If there are mistakes, they are probably caused by my lack of skill with the algebra. In any event, the original simultaneous equations may be what determines how the number of dimensions are decided. I can't really tell. -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
damned if I know- 93 replies
-
-2
-

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
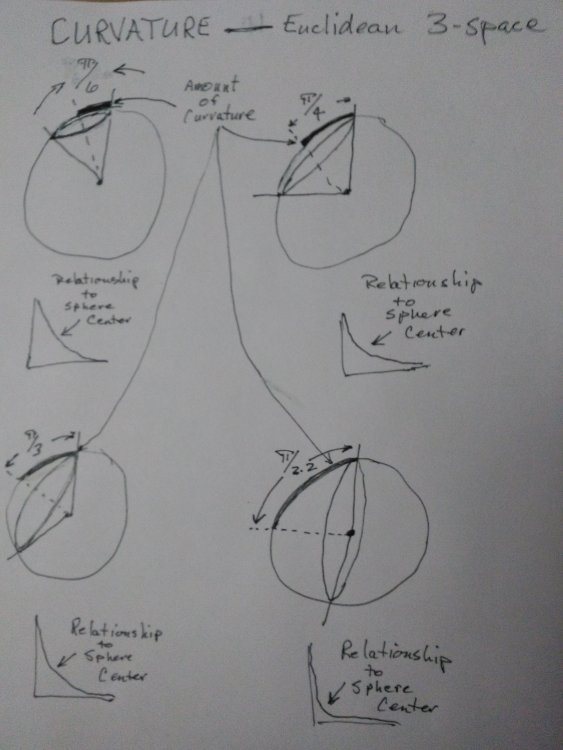
there are three angles represented by Greek letters these three angles can either exist in two dimensions (co-planar) or not when they are not in the same plane it is an identity -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
When the three Greek variables exist in three dimensions (the set of Greek variables) it is an identity. When the number is reduced to two (when any of the three dimensions is zero) the identity does not exist.- 93 replies
-
-1
-

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
Correct. It is an identity in three dimensions. It doesn't exist in two dimensions. Correct.- 93 replies
-
-1
-

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
The way that I understand it, when time is removed from spacetime we are left with Euclidean 3-space. What we are talking about when we use state-of-the-art math is really a model where we have x-y, x-z, and y-z planes arranged orthogonal to one another. The geometric rules that apply in any plane are the same as with any other plane, and these geometric rules are consistent with trigonometry and Pythagoras. A much better nomenclature for this type of construction would be 2D3, or 2D x 2D x 2D. This is what yields our octants, this 23 relationship. As this is continued further then we get 2D4 or what I believe is called a 4-dimensional manifold, or what you might call 3D+1 or what others might call R4. This further doubling of the divisions is what causes the need for imaginary numbers, as was pointed out by another member above. We assign time to this last "2D construction" (clarification to follow) that is added, but we have to treat time differently than we do the other "dimensions" because time is a different quantity than distance or length, which was the only quantity that was contained in the first three 2D constructions or planes. The reason I say “dimensions” in quotes is because in physics the term can have a completely different meaning. It can also be used to distinguish between different quantities such as distance or time or temperature or mass, etc. There are currently seven of these base quantities that can be mixed and matched in certain ways and that fall under a basic branch of math/physics called dimensional analysis. In this context each different base quantity can be called a dimension. Where it gets really complicated is when we need more than one instance of any particular base quantity in order to represent a physical phenomenon. For instance, in the current state-of-the-art model of spacetime we need three instances of length and one instance of time. This is where we can clarify the reference above that talked about time being a "2D construct." Obviously, since time only exists as on instance of the quantity in spacetime, it doesn't need to be combined with itself like distance does. Therefore it differs both mathematically and conceptually from the way distance is considered. That’s probably why time has been selected in the mathematical treatment to get the imaginary coordinates rather than any of the other length “dimensions.” Being aware of this reality, it is fairly difficult to stay on track with our terminology. I am currently trying to stay in context with the terminology that was introduced in the previous thread about surfaces in a higher dimension. Try and see the symmetry of what I’m talking about. This symmetry is a very fundamental connection, far deeper than the few associations that are necessary in order to add or remove orthogonal planes from a particular geometry as is done with Rn+1 or Rn-1 and so forth. In the Cartesian system we can begin with three axes and then divide each axis into identical units. This does not get us completely to where we want to be. We have to make it axiomatic that the three axes are at right angles to one another. Direction is an axiom and distance is a quantity, or what we call the metric. Consider the opposite arrangement. We have three axes and we connect a point on each axis with a point on the others and we make the angles between them identical angles. By this I mean that the angle formed by each axis with each connecting line is the same. This arrangement is perfectly symmetrical to the identical units in the first example. We still must make something else axiomatic in order to achieve orthogonality. This time we must make all these connected points equal distance from the origin. Instead of equal right angles as in the first case, we have to assign equal lengths to each axis. In either case, the expressed quantities are only one half of the picture or reference frame while the other half of the picture, the given or axiomatic quantity, is already baked into the system. It is possible, in Euclidean 3-space, to construct a reference frame that utilizes direction or orientation as the expressed quantity. In this symmetrical system, length will be axiomatic and without orientation. Think diameter of a sphere. It is a length without direction. In this additional view of Euclidean 3-space, a vector becomes the symmetrical opposite of what we are used to. The direction is the magnitude or scalar value while the vector becomes the magnitude and length. I know it sounds extremely weird, but it’s only math. Try the math. See that it works. If I had the algebra skills necessary to write this all down algebraically I would continue to do the math and take it to the next level. But I’m pretty sure that I’ve gone as far as I can without more help. The mathematical identity is the key to understanding all of this. This identity is something that we just stumbled across while trying to solve some different problems. We were able to recognize why it is so significant and precisely why it differs from all of the other known geometric identities. The first step in problem solving is recognizing that there is a problem. It should be clear to everyone that our current understanding of spacetime has some issues. I believe the math that has been done so far shows that the problem is with how we are doing the geometry. The standard methods overlook some very basic things that must be included in order to represent a curved spacetime model more accurately. As a matter of fact, it was once argued by some members that there was no underlying function to the new model, but that argument was dropped when the algebraic expression for the function was produced. Then it was argued that there was no new identity, everybody move along, nothing to see here. Just high school math that could be accomplished in an afternoon. Now it is being argued that the new identity is not significant to relativistic transformations, even though this was the original claim. At some point the light will come on for someone. The identity expressed in the OP must be included as part of any accurate representation of Euclidean 3-space. Until now, omitting this fundamental element of Euclidean 3-space from our models has never been much of an issue. It’s only when we try and take a close look at curved spacetime that the problems with maintaining this identity become realized. Maintaining this identity in any more accurate model of spacetime is not an easy undertaking. It’s a daunting project. But it must be done in order to make the math work out correctly.- 93 replies
-
-1
-

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
There are fundamental rules (Pythagoras and plane trigonometry) that are associated with 2 dimensions. Moving from R2 to R3 simply adds an additional set of these exact same rules, arranged orthogonality, to the single set of rules that already exists. Do you understand this? Also, it can be and has been shown mathematically that a completely new set of rules applies to R3 that cannot exist in R2. This set of rules are in addition to Pythagoras and plane trigonometry. Do you understand this? I'm trying to drill down on some way to explain this to you. Either you follow me this far, or you don't and I'll have to back up even further. Close, but using your analogy the transition to Euclidean 3-space adds an additional physical attribute or quantity. It's analogous to adding color to your 2D(+1) construct, in addition to your usual geometric relationships.- 93 replies
-
-2
-

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
You are mistaken, especially in your ad hominem argument. I have never made the admission that you attribute to me. Yes, I am one of those self-taught geniuses that has never had any use for algebra or any of the other standard bookeeping methods. I generally use my own shorthand, which does complicate things a great deal when trying to explain this problem. Once again, the math is either correct or it isn't. Its accuracy has nothing at all to do with my understanding of trig or algebra or anything else. It has nothing to do with me at all. The one dimension that you're transforming isn't what you think it is. It's either no longer orthogonal to anything or its metric has changed. Do the math. If you have questions about the identity above then please ask.- 93 replies
-
-2
-

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
The point of this thread is to point out that the intrinsic curvature is not accurately captured by the current methods. Trust that I understand the current method and that you don't really understand the identity above or why it shows that the curvature is more than what flatlanders can see. First of all, I'm not sure what it is that you want a demonstration of. And secondly, my ability (or inability) to demonstrate something other than what I am claiming has nothing to do with whether or not my claim is accurate. It’s math, it’s either correct or it isn’t. I appreciate that you have at least tried to work the math yourself. It would greatly facilitate this discussion if someone other than me would try and verbalize what they think the identity above means. That way it might be easier to assess where to focus the conversation. If the identity has no meaning to anyone then I’m pretty sure that nothing that I can say will make any sense at all. -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
The Lorentz transformation doesn't maintain this relationship. I seem to be the only one who sees this or thinks it might be important. -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
Everyone except me. -

Additional Question About Surfaces in Higher Dimensions
steveupson replied to steveupson's topic in Mathematics
It's hard for me to imagine the usefulness of a mapping that loses so much information about position (in 3D) when we are trying to understand position (in 4D.) Why would a mapping that doesn't contain this relationship be relevant to physics? edited to add> I can understand that it may not be relevant to Galilean spacetime but it doesn't make sense to me that it isn't relevant to relativistic spacetime. -
In another thread on this subject it was stated that “we can establish a one-to-one mapping between any Rm and any Rn.” There is a relationship that occurs in R3 that I believe cannot be mapped to R2. The relationship exists between the sphere center and the surface curvature. I believe that because R2 has no third orthogonal plane or axis that this relationship does not exist in R2. This is best described as a relationship that exists between the tangent to a small circle on the surface of a ball and the gross position of the ball in 3-space. The illustrations show how this relationship can be seen. Mathematically, it is expressed as an identity: [latex](\cos\frac{\phi}{2}\:\sin\frac{\lambda}{2})^2 +(\cot\frac{\phi}{2}+\cos\alpha)^2=1[/latex] Does the fact that this mathematical identity exists and is not represented in the current mathematical approach to modeling spacetime have any significance? To me it seems that this isn’t an issue unless the spacetime is curved, at which point it appears that the whole idea of using Rn-1 breaks down. Why isn’t this the case?
-
angular speed is the same, linear speed is greater