Sandor Szekely

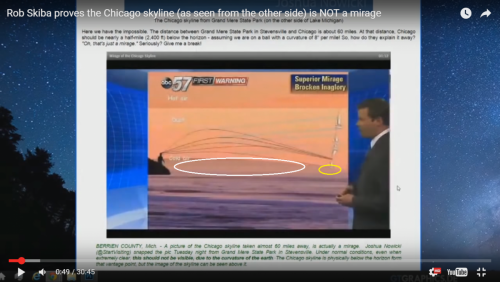
I have explained reversed direction of refraction so far and as well why I think that it playes no role in the measurement outcome for the side note: you can not detect the curvature from a airplane - this is a typical misconception http://thulescientific.com/Lynch%20Curvature%202008.pdf

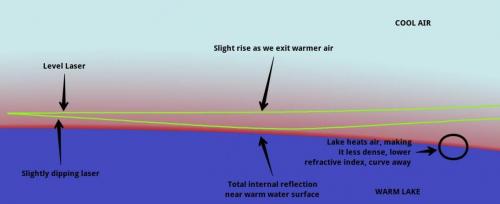
8 centimeters / miles is misleading 1.25 is well understood as we speak in meters in the whole film Well we ALL don't have to agree as it is quite impossible too. We do talk about refraction in the video as if there is any possible refraction of the laser beam it is bending upwards as we have reversed atmospheric conditions at dawn than in the afternoon when the mirrage effect is possible to detect. Look up terresterial standard refraction (value 0.4 millimeter / kilometer). We have marginal refraction that is upwards - I am not calculating with it. We had the laser at 1.25 meters that is 4.1 feet that is NOT close to the water level and outside the NUDTZ non uniform density transition zone

Hey Studiot I am back - the veil lifted on me so far: I agree that the refraction effect is marginal and bendig upwards direction so this will not effect the outcome of the experiment at our accuracy. I think we should discuss the measurement accuracy: we have a difference of meters on the longest distance measurements. to the other comments: Please ask questions, and be carefull to use exact definitions and numbers (I am refering to curvature drop at 8 INCHES / miles squared)

Thank you for your post#9 which begins to describe your methodology, but more is needed. As I understand it you are extrapolating, rather than interpolating your corrections. I further understand you are applying standard corrections at the end of a 720m observation line, although I am not familiar with the GE model. Standard close to the ground (water) surface observations like these are subject to curvature and refraction corrections. Yes I agree with 4cm for the curvature (I make it 41 mm). John is correct in noting that there is also a refraction correction, that I was coming to as it is more minor. The standard refraction correction, is equal to one seventh of the standard curvature correction ie 6mm. This make a total correction over the observed distance of 34mm. Both of these would be eliminated by suitable interpolation methodology. To return to the implications I mentioned earlier, Using standard curvature and refraction corrections it would imply a bulge (see attachment) in the Earth land surface in this area, which should be detectable by land surveying techniques, as opposed to hydrographic ones. This is entirely feasible since most of the lake is only a couple of metres deep old fashioned 10 foot survey towers could even be used. Alternatively (1) There could be an undisclosed error in the methodology (2) There could have been freak atmospheric effects causing effect at the time of measurement. obs1.jpg Hello John nice to meet you Actually we made a complete video explanation of our measurements that includes all the correlating subjects - like refraction - but not allowed to quote it here. This makes me explain my points much more harder and I have this post only (max 5 replies) - well kinda hard to debate the subject. I will try to answer the upcoming questions by editing this reply. Jon: "That make light bend down slightly as it goes through the air and throws the calculation out slightly" Refraction is not bending light downwards in our conditions, but UPwards - as the lake temperature is warmer (22C) than the air above (17C). We choose all our measurement timeframes in such ambient conditions where the refraction effect is bending the laser beam upwards, so this would make the refraction corrected height even worse for the GE model. Indeed we did not experience any significant refraction of the laser beam in any of our 4 measurements at the last experiment. The standard value of terresterial refraction in normal conditions (daytime) is 0.4 millimeter / kilometer in geodezy. The refraction of the beam was not detected and it must have been within our measurement accuracy. (waves, measurement precision) The GE curved water surface and the FE flat water surface model has a much more significant difference in expected height difference than our measurement accuracy. John: "It seems you are in danger of repeating a 19th century mistake." Are you refering here to the Robowham or the Wallace experiment? We had our laser at 1.25 meter (4.1 feet) at the last measurement - that supposed to be over the N.U.D.T.Z. ( non uniform density transition zone) Studiot: "As I understand it you are extrapolating, rather than interpolating your corrections." "Both of these would be eliminated by suitable interpolation methodology." Please explain this to me in more details. We are continuing our measurements over the lake and land surface as well, so we can fine tune the measurements in the future. Now we had our measurements taken by photographic evidence and evaluated by photo analysis. This gives us a pretty accurate reading for us way within the accuracy needed to make a conclusive measurement. This time we did not have the possibility to use geodezic equipment as you suggested, but we will do in the upcoming ones. "Using standard curvature and refraction corrections it would imply a bulge " As I wrote to John, the refraction of the laser beam would be a reversed effect to curve the beam upwards, and not downwards. In that case we should have even a greater difference in the models and would make the GE calculation worse. We had the laser beam at 1.8 meters height above water surface at the distance of 6kms. If refraction would account for let's say 0.3 meters upwards curve than that would make the measurement 1.5 meters above water level. This was not the case here, the FE flat water model just fits perfectly with the 0.005 degree slope correction applied to the laser leveling. We had the laser beam height just as expected on the truly level water surface. This is exactly the same outcome as the airborn LIDAR experiment. Studiot:"It should be remembered that the observation lines we are talking about are not tens of kilometres long with associated hundres of metres of correction. This as I said, was the overdaramtic headline stuff." The hypothesis of GE curved surface water model states that the curvature drop is 465 meters on the 77kms total width of the lake Balaton. We will be probably able to measure this complete distance in the winter time when the lake is frozen. This is a picture of the lake frozen - this should have a 465 meters curve on the surface: AS a new member I have a limit of 5 comments in the first 48 hours... still bout 12 hours to go! (this is insane by the way... not to be able to comment correctly on my own thread) Sorry I had a lost message just before, when I restored it from saved it messed up the quote signs maybe... I had to retype the half of the message again. Studiot: "I am interested in you methodology because of your apparent claim that the water surface is flat over a distance of 77km, yet is only a couple of metres deep. Therefore the lake bed under the water must also exhibit this characteristic. We have both agree that the deviation from a spherical surface over this distance is of the order of several hundred metres. Since a 3m layer of water apparently exhibits this, the lake bed underneath it must also exhibit this. Hence the bulge. I have repeatedly asked you to clarify this point and you have repeatedly avoided it." Studiot please clarify what should I clarify here? The hypothesis of GE curved water surface model is 465 meters over the 77kms distance as we agree. The measurements were taken upto 6kms distance and we found no curvature drop yet. The LIDAR experiment had the same outcome: "the two data systems confirmed that standing water has a truly level surface" (page 8/15 in LIDAR pdf) Studiot: "Arguing about whether a minor correction of a few millimeters to several hundred metres is upwards or downwards is irrelevant." I aggree with this absolutely. Refraction of the laser beam played no significant role in the measurement. Sorry to everyone, until I do not have my ban lifted I can not answer any comments. It may be the problem with my account by I had this message yesterday: AS I am also not alllowed to edit my comment here many times - I have to wat 12 hours from now. Admin, if you can please do something about it.

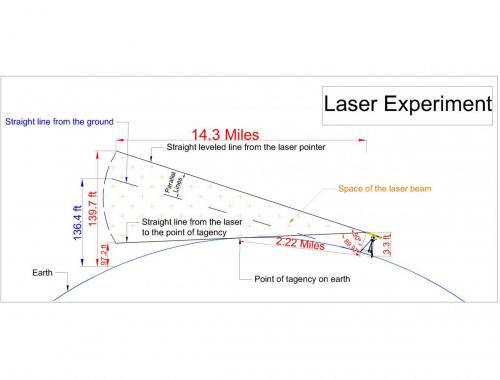
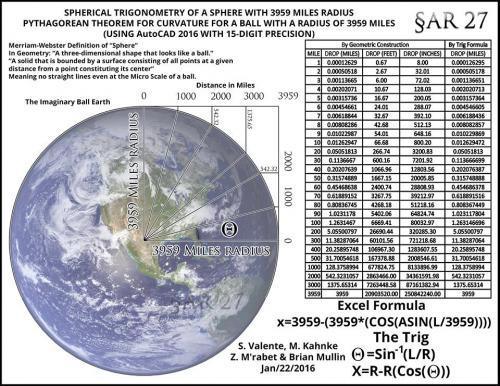
Well it's not our intention to use "a bit of theatrical dramatics" but this is the correct way to calculate the expected height of the laser beam on the opposite shore. We calculate the expected laser height as: Drop over distance + original height of the laser. We use a slope correction method at the leveling distance of 720 meters to make a true horizontal level to a 0.001 degree accuracy at the position of the laser on the shore. We do tht by adding a 4 cms to the original 1.25 cms laser height to set the beam level on the boat, as the GE curved surface model has a 4cms drop in this 720 meters distance. This is the method and setup that we used at the 4th measurement of the 2016 aug 16 experiment. Here I show an example of our 14.3 miles distance calculation (upcoming experiment) The expected height of the laser beam shall be at 139.7 feet on the GE curved surface model. On the GE curved surface model the beam must not be detectable below 97 feet in any possible laser leveling method.

Studiot, your calculation is the saggita as I see. The question here is: what is the drop of curvature over the 77kms distance. This means how tall object is in level to the original starting position on the curved water surface model. You gave answer to the how high should the water bumb be in the middle. In an other way how deep the laser should go into the water to reach that height at the other shore. We use autocad to calculate the exact drop over distance, but most of the online calculators give the same result. I have a math from the Hungarian ELTE university: h = (0.28 * s)'2 where h = height in meters s = distance in kilometers We made this calculator for imperial units: You are right by saying that the lake is indeed a thin surface film, and therefore it should follow the curvature of the earth as it has no depth to compensate with as the water takes the form of it's container. We should be measuring the expected curvature on the water surface.

Thank you Studiot I will do so as the links were taken out of the thread. I will include now the text version to the thread - can I do that?

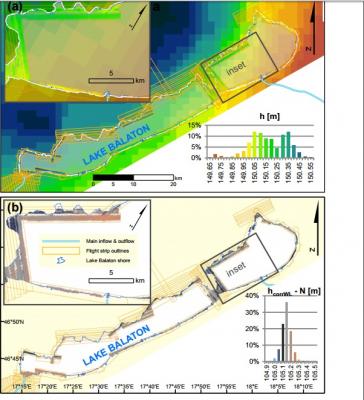
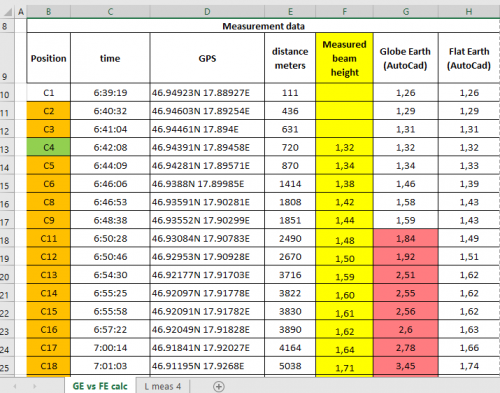
Dear Visitors we would like to introduce you our laser curvature experiments. We are looking for the curvature on the surface of the lake Balaton in Hungary with special laser technology to detect the supposed curvature on the water surface. How much is the curvature of earth on the distance of 77kms? (47.8 miles) 465 meters! (1526 feet) that means that an object this tall in one side of the lake must not be seen from the other side. Online curvature calculator: https://dizzib.github.io/earth/curve-calc/?d0=47.845581802249&h0=0&unit=imperial But is that assumption of GE curved water surface model true? We have conducted a series of experiments and surveyed Lake Balaton in western Hungary, which is a shallow (average depth 3.3 m), large (597 km2 ) area. To what extent does the lake resemble a level surface? The airborn LIDAR laser scanner measurement in 2013 Figure 2. (a) Map of lidar-measured ellipsoidal water surface heights (inside flight strip outlines) and modeled gravity potential isosurface height (background raster) with the same elevation color scheme. Inset shows detailed height distribution of water surface measurements, histogram refers to lidar measurements (not to gravity potential isosurface model). (b) Map of lidar-derived normal water surface heights, obtained by correction with local deviation of LMLL and local quasi-geoid height. Histogram refers to water surface normal heights. On Lake Balaton, currents are driven by wind forcing and by seiche while thermal convection remains hardly observable (Muszkalay, 1973). The flow of water from the tributaries towards the outlet is also very weak, because significantly more water leaves the lake through surface evaporation than through the outflow. The rule of thumb for air pressure response is 1 cm decrease in water level for 1 mbar increase in air pressure (Ponte and Gaspar, 1999). However, this only applies to the open ocean and after a period of 1–2 weeks. Since the lake was very shallow, most of the air pressure is directly forwarded to the lake bottom. Therefore we assume that air pressure changes could not have influenced the local lake level Lake tides are known to have amplitudes of up to 10 cm in larger lakes (Trebitz, 2006). In case of Lake Balaton, the shallow depth and the relatively low water volume of the lake suggest this effect would be even smaller. Due to its fresh water, shallow depth (3.3 m avg), limited in- flow and small water volume (2 km3 ) compared to its surface (600 km2 ), Lake Balaton experiences very limited variations in water density. There is no thermocline, warming and cooling can only create maximum vertical temperature gradients of up to 1.1 ◦C m−2 , and horizontal differences in surface temperature between basins have been documented to remain less than 3 ◦C (Virág, 1998). The salinity of the water is also quite constant over its area and over time, so no major changes in density are expected. The height effect of local warming or cooling can dissipate relatively quickly on this scale, therefore no contribution of density change to lake topography can be expected. Both in the cases of the 2013 LIDAR experiment and the 2016 laser experiment confirmed that standing water has a truly level surface. The result of the new 6kms laser measurement are shown here in the data sheet. Note: that the GE model curved water surface expected laser beam height does not match the observed height. The accuracy of the test is negligable to the difference of the calculated and measured value. Balaton-laser-exp-816-data-sheet-4th-measurement final.pdf OUR NEW 6kms laser measurement: youtube links deleted The airborn LIDAR measurement http://publik.tuwien.ac.at/files/PubDat_228814.pdf The pre-test video Here is an other new video from Mr Thrive and Survive youtube channel - talking about our new 6kms laser measurement: Please ask questions