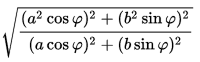DarkStar66

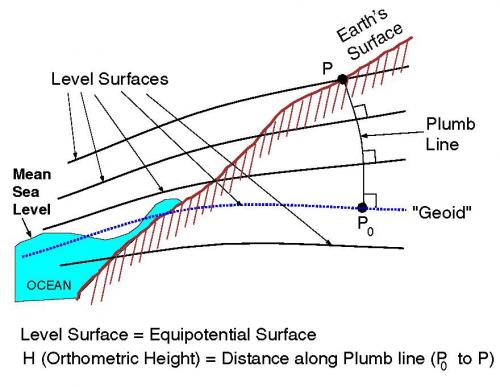
My 2nd image is from https://www.ngs.noaa.gov/GEOID/geoid_def.html So I'm excited to see your alternative and we can tell the folks at the National Geodetic Survey they are wrong The definition for 'level' as shown is "tangent to an equipotential surface of the gravity field" which is exactly what is shown on the diagram by the right angle indicators on the plumb lines. Or are you objecting to my diagram showing "flat"? There is no geodetic term 'flat' so I've used the colloquial. Would like to close that question out.

Maybe these will help... Level doesn't mean flat: And with some exaggeration in scale, showing that level also is lumpy:

I didn't make any hydraulic predictions, I agree with your assessment on that front. I make no attempt to model those. I agree you need to actually make the measurements. I would also note that I just did a couple of things -- I took Sandor's EXISTING spreadsheet (don't know if you realized this or not but that wasn't my original spreadsheet -- this is the one that Sandor had published with their 'experiment') and I replaced the spherical approximations they had used with the the ellipsoid approximation, and I tried to guesstimate how much the beam was actually spreading out over the distances. Sandor is the one building the model, I'm just trying to show their original had significant issues. Unfortunately, for all the reasons I mentioned previously, we really have no usable data from their 'experiment' to compare it against. I think that would be fun even if we had issues. Even reading what you have written I'm not sure why you think the shape of the lake cannot be modeled accurately enough for the task at hand -- Sandor's goal is not to get an accurate survey but rather to prove that the lake is absolutely 100% a Flat Plane on a Flat Earth. And he believes (and has repeatedly stated in this thread despite the PI on the study explicitly stating that this is not the case) that the cited 2013 study claims the lake is exactly this 100% flat plane. So the question is -- do you think we can model the curvature on a Lake "well enough" to fit some observations that show it is not flat? I think over a large enough distance with proper techniques this is easily done. But the real problem is their laser isn't up to the task even if we had a perfect model to compare it against. You can't make "hide nor hair" of the laser past C5 and since they pointed the laser on the board at C4 that's as good as having no data. And the laser spread at C5 at 870 meters is already all but unusable (I would say even that is unusable)... you tell me: Ignore that the board is slanted -- can you read a reliable "height" from that? Even if everything else was known perfectly? That said, the distances calculated ARE based on great circle distance calculations between lat/long points so they are already spherical distances. However, the measurement error for the lat/long readings FAR exceed the difference between "straight-line" and Great Circle distances over 6km. After showing their first data point at C1 wasn't 111 meters from the laser but 1.9 meters I have zero reason to trust their GPS data either. Let's do a quick sample, assuming a circle. The straight-line distance given s=curved distance would be R*2*sin(s/R/2) So for s=10km distance 6371*2*sin(10/6371/2) = 9.99999897347 So 10 km spherical distance is just 1.03mm off on the straight-line distance. We're not getting 1mm accurate GPS coordinates here, we're getting +/- several meters. My main point has been that NONE of their measurements are valid for a multitude of reasons and I've tried to highlight some of them. There are so many it's hard to hit them all. But from his comments Sandor still refuses to accept that the laser is spreading out.

Yes it is, look at your data more carefully, already at C11 it's all over the board and glinting off the water. It's just very dim because it's spread out so much. This is easily 3 meters of spread already if not more. I've enhanced the color separation so you can see the green laser light very clearly. And you can look at your beam diameter at C2, C3, C4, C5 and see it heading that direction. These earlier measurements show that the beam is spreading wildly out of control. I have no idea if it's 12 meter or 30 meter by C37 - that's why it's labeled extrapolation, however, it's irrelevant because I show that none of you measurements past about C8 are even close to reliable based on what we can see. The real point here is that you have no way to show that I'm wrong. You have to present the data to validate your measurements. What I'm showing is that what you have shown is simply not reliable and I've shown why (in great detail which you have mostly ignored). Since the beam is spreading both horizontally and vertically the metal support frame wouldn't be the cause -- that would only contribute to vertical reflections. C4 obviously is but taking your intention here please note that I do not use C1, C2, or C3 as a height measurement point - In fact, I specifically point out that you MOVED the laser at these points and so they are invalid for this purpose - I calculate the slope based on 1.25m laser and point C4. They ARE however valid observations of the beam divergence and I use them for that purpose. I showed and measured the obvious beam spread in the images. Why don't you take your images for C1, C2, C3, C4, C5 and you tell us how big your laser spot is at each one? Sandor -- the most critical error so far, which was raised by maximillian12 on the 18th, is that the ellipsoid shows a 17m delta over the 6km distance. Ideally Zach should remodel your 'GE Model' using this ellipsoidal data -- as I did in my spreadsheet -- and then you guys need to admit that most of your data past about C5 is very poor due to mismeasuring reflective spots on the boat (as you've not yet responded to any of that, see linked post). Please note that my spreadsheet is only PRELIMINARY and is certainly open to review - I don't claim they are perfect. If you find an error point it out and we can discuss. But which one do you not understand specifically and I can discuss them in more detail? Let me point out some of the data locations and overall calculations: Ellipsoid calculations: J3 = WGS84 ellipsoidal flattening (f) J5 = WGS84 ellipsoidal equatorial radius (a) J8 = equation (approx) used for Ellipsoidal Radius of Curvature at latitude θ: a(1-f sin²(θ)) Laser/beam spread calculations: O7 = Laser Height (1.25m) AGL (above 'ground' level) Q5 = equation for extrapolated beam width: c*e^(bx) Q6 = value for c - from INDEX(LINEST(LN(Q12:Q15),LN(F12:F15)),1) Q7 = value for b - from EXP(INDEX(LINEST(LN(Q12:Q15),LN(F12:F15)),2)) Where Q12-Q15 are the measured spread values, F12-F15 are the associated distances R7 is your starting aperture, I've used 100mm R8 is the equation used for 1/2 angle divergence (atan(g/d/2)), where g = beamwidth-aperture, r=distance(column F) (*1000 for mRad) S8 gives the equation for 1/2 beam spread (d*tan(a)-mm/2), where d = distance(column F), a = 1/2 angle(column R), mm(aperture)=$R$7 -- but this is also JUST half the beam width, I did it the 'hard' way as a check on the math for divergence angle - so basically S=Q/2 As for where these formula come from, they come from basic trig: tan(α) = a/b This says that tan(α) gives you the slope of c, a=rise, b=run, slope=rise/run -- conversely atan() takes a slope and gives you the angle back. We can apply atan() to both sides: atan(tan(α)) = atan(a/b) which simplifies to: α = atan(a/b) Now, in our case, a is 1/2 of the diameter -- so that's why you see atan(g/d/2) -- and we subtract out/add back in the starting aperture of 100mm (0.1m) (or 1/2 that for the 1/2 spread) -- essentially treating it as a point source in the middle. Feel free to give us your equations for beam spread. P7 is the Slope calculation: (K14+N14-O7)/(F14) -- which is: (ΔGround@C4[2.286] + EstMid[1.185] - LaserHeight[1.25]) / Distance@C4[720] Column O is not used, but shows the spherical curvature approximation over distance (column F), given r=6371000 We calculate the Ellipsoidal Radius for column J using the values f and a from WGS84 using your given latitude values in the spreadsheet. I use an approximation function (as stated in the spreadsheet: a(1-f sin^2(θ)). If you want to use the more accurate equation use this: ΔGround is simply the total change to that point in the Ellipsoid radius in column J (=J10-$J$10) - this shows the ~17m change in radius of curvature over the 6km Then you need to show us the evidence you promised a while back. I have shown mine. "est mid" at C4 is 1.185 which is from Mick's calculations BOTH on the pixels and looking at the slope of the board from numerous lines of evidence. You still haven't provided any evidence that your measurement of 1.3m for the top of the tape was correct. I also looked at the dimensions of your exact boat plus the height of the board at the observed angle. It all points to ~1.185m for the top of the tape, not 1.3m. If you are hoping to approach scientific accuracy on this experiment then you need to take this seriously. You just keep denying that this is a problem despite the significant evidence against it and no evidence supporting your claim of 1.3m. Est Beam" is just the estimate beam path, this is simply based on the slope, ΔGround, and laser height. Calculated Bottom of Beam is beam path plus taking into account the radius of the beam width. summary of issues: need to use ellipsoidal model, not spherical need to account for 1.3m height measurement - measurements must be dead accurate and supportable need to account for the observed beam spread (C1, C2, C3, C4, C5, C11 show evidence of significant beam spread) cannot use 'direct hit in camera' as a valid measurement (C31 example) cannot use reflective spots on the support bar on boat as valid measurements (C5, C11, C19 are the same spot, but you marked at different heights) cannot use reflections off jacket reflector as a valid measurement (C13, C14, C16, all the same jacket reflector, but again, all marked at different heights) cannot use glints off the camera lens as valid measurements (C17, C18 are both camera lens glints but marked at different heights) Additional notes on other comments: I agree that in the night-time video the most likely explanation is that the laser was hitting the water and reflecting upwards and while very pretty & interesting in other ways, isn't relevant to the test results labeled Laser 4 or indicative of refraction effects. The email from András Zlinszky makes it very clear that their results are in no way consistent with planar, flat lake. You keep using this sense of 'level' that is not used in the world of Geodesy. http://nptel.ac.in/courses/105107122/modules/module1/htmlpage/24.htm You also made this comment in the thread: You seem to be confusing a gradient in the orthometric height of the terrain (which would cause water to flow) with the geoid -- these are not the same thing can cannot be compared in this manner. The geoid shape can vary and water will not flow, but will conform to the geoid shape as long as other forces are not acting upon it (tides, winds, etc). This shape is defined by the slightly lumpy gravity of the Earth and its spin (which cancels out a very small portion of the Gravity and varies with latitude, highest at the equator and zero at the poles). When you give an elevation from a map, you are usually giving the Orthometic height or the closely related, MSL height. So a change in THIS height means water flows. But a 100m rise in the Geoid does NOT cause water to flow. The shape of the gravity equipotential is what defines 'level' at every point. That's why, even though the South end of your path over the lake is 17 meters further from the center of the Earth than your starting point, every point along that line is 'level' even though the water is 17 meters higher. This change does NOT cause water to flow and you do not feel it or measure it as "going up hill" because it's a gravity equipotential. It is this gravity equipotential shape that the water has conformed to. That shape just happens to be 17m higher on one end than the other. Some definition of terms might help: Geoid: The geoid is the shape that the surface of the oceans would take under the influence of Earth's gravitation and rotation alone, in the absence of other influences such as winds and tides. This surface is extended through the continents (such as with very narrow hypothetical canals). All points on the geoid have the same gravity potential energy (the sum of gravitational potential energy and centrifugal potential energy). The force of gravity acts everywhere perpendicular to the geoid, meaning that plumb lines point perpendicular and water levels parallel to the geoid. Orthometric Height: The orthometric height of a point is the distance H along a plumb line from the point to the geoid. In my spreadsheet I ignored the Geoid height because it was constant to 1cm and saw little point in adding it in only to subtract it back out. Essentially the shape of the water matches very closely to the Ellipsoidal shape so we just need to know how much THAT changes, the rest all cancels out to within 2cm. If you want to be MAXIMALLY accurate, then you need to download the software and data sets for the Geoid, and Orthometic heights and get exact data for your measurements points (and measure actual depth of water since that would be a variable), that will get you an additional 1-2 cm of accuracy for your 'GE Model' (aka Globe Earth).

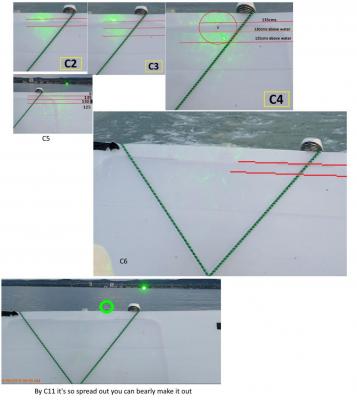
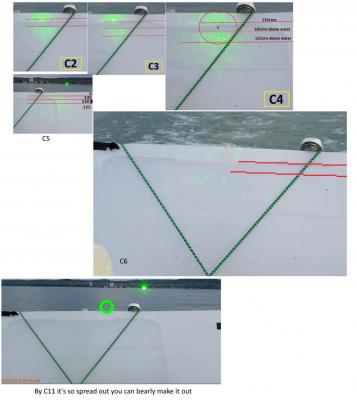
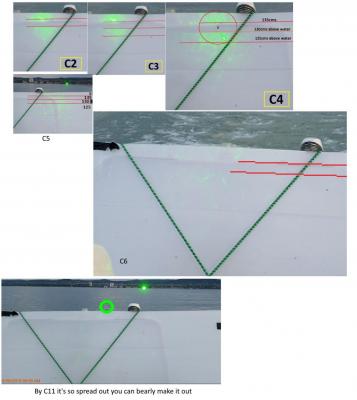
Here is my first stab at putting this into a spreadsheet: https://drive.google.com/open?id=0B22sA7_PYGQvMFY5WWtIenU0ZVk Assumptions: WGS84 ellilpsoid f=1/298.257223560 a=6378137.000 Radius of Curvature at latitude θ ~ a(1-f sin²(θ)) That the top of the black tape mark is ~1.185m as estimated by Mick West's analysis. The slope calculation is against a flat baseline calculated between the laser itself and measurement point C4, where they re-leveled the laser. ΔGround[2.286] + laserHeight@C4[1.185] - laserHeight[1.25] / distance@C4[720] = ~0.003084 meters per meter You can use column T to ignore the beam width or column U attempts to find where the bottom of the beam might be. Beam divergence angle for C0, C1 is just set to same value as C2 as I don't have good values - the values in green are actual estimates, the values after that are extrapolated but conservative estimates from the green values only. No refraction is taken into account. Unfortunately the data is not clean enough to do a 'fit' analysis. But this does align well with the first few measurement points, accounts for the beam spread and later reflective hits. Using simple curvature did NOT fit the observations well. Thank you. By 'Gaussian beam divergence' I just mean the amount of divergence expected from a laser beam given some degree of collimation, even in a vacuum. This beam is spreading at an increasing rate of divergence rather than some fixed divergence angle. So I think that atmospheric effects are dominating. Some of that is diffraction, some is refraction - but end result is that the spot we see at C1 and C2 has grown considerably by C4 and by C11 it's so spread out we can barely see it on the board. If you assume an ~100mm aperture (hands width) at the start and try computing the divergence angle at each of C2, C3, C4, & C5 you get different answers for each distance -- so it's not a constant rate of divergence (or maybe the distances are wrong but I think it's too great for this to be the only cause). These are the measurements that I'm referring to and I posted a montage showing these in my earlier post: 426m shows ~25cm diameter of spread 631m shows ~31cm diameter of spread 720m shows ~48cm diameter of spread 870m shows ~72cm diameter of spread

I made a chart using Excel based off the ellipsoidal equation for radius given latitude using the latitudes given in Sandor's provided Excel file. r(θ) ~ a(1-f sin²(θ)) (see here) I immediately ran into an issue because they stated the laser was at 46.94922N 17.88929E and their first data point is at 46.94923N 17.88927E and is given as 111 meters distance, but this point is only about 1.9 meters from the 'laser' coordinates. So the data is clearly wrong here. I used ESTIMATED coordinates for the laser of 46.950048N 17.888435E to make it 111 meters away. The results are (with greatly exaggerated y axis) very similar to yours: Or about 17m across the 6km of the lake. Which is very interesting as that means that while the far side of the lake would be an ~2.87m 'drop' from a tangent (on a perfect sphere) due to curvature, there is a ~16.7m change due to ellipsoid? Did I get that right? That seems to be pretty significant in terms of this measurement. I checked the WGS84 Geoid height and it was a pretty even 46.3 - 46.29m across the lake coordinates (as you would expect for a body of water) - so that should mean the Ellipsoid is roughly the correct shape. I agree that marking this up in AutoCAD would be very interesting, instead of using spherical approximation. But given the very large and evident spreading of the laser Where I estimate these values: at C1 = 111 meters, beam is 25 cm (diameter) at C2 = 436 meters, beam is 35 cm (diameter) at C3 = 631 meters, beam is 48 cm (diameter) at C4 = 720 meters, beam is 72 cm (diameter) Beyond that the beam is so spread out we can barely see it and cannot accurately estimate the diameter, other than to note that by C11 and C12 we can just barely make it out as covering a substantial portion of the whole board (enhanced contrast in the image below shows it more clearly). This is showing beam spreading far greater than Gaussian beam divergence. Combined with the unreliable methodology used to gather the height measurements as I show below where you can see they are marking the same few reflective spots on the boat at ever increasing heights, even when the reflection point moves to a lower point on the boat they marked it higher (see C19 case): And since the calibration height at C4 was seemingly incorrectly marked, the 'leveling' height above the water is questionable as well. So I don't think we can really get any data out of the prior experiment. I've been trying, you cannot get a reliable height estimate even at point C5 - see: Even if I very conservatively model the beam spread past C5 I have a 12 meter wide beam on the far side of the lake. This swamps out any possible measurement because we repeatedly only see specular reflections from the bar, the reflector on the jacket, and camera lens glints. So this is just a rough attempt to capture the ellipsoid into the data along with the estimated slope taken at C4. Now the interesting thing is that previously I was working with just the curvature estimate and the results did not align with observations -- this suddenly made everything snap into place up to about C11 which is really about as far as I can make sense of anything. This is using C4 as a true height of about 1.185m instead of their 1.3m and slope is calculated from there. I'll try to put my spreadsheet online somewhere to share it as this is very interesting.

It also makes it sound like they tested the whole 77km in their video but didn't, not even close. Yet still proclaimed it as "100% proof". You guys are all talking about advanced calculations and measurements but have you watched their video to see just how badly this was done? These guys believe that just because a camera on the boat can merely see the laser on the dock as a bright spot that this constitutes a valid measurement of the center of the beam height. I've posted clear evidence that the beam spread was out of control but you can see in his responses that Sandor doesn't even understand that anything was wrong or take this seriously. Please consider beginning by trying to convince Sandor that just because a camera on the boat can SEE the laser looking back at the dock that this doesn't constitute a valid measurement of the beam center. I would think such fundamentals could be easily agreed upon. Direct simple question: Sandor - based on what has been discussed about this data do you still consider your data point measurements to be valid and mostly reliable and accurate?

This shows the beam spread progression from C4 to C11 (1) that was already shown in the video very clearly (2) I'll wait for the evidence - you can send me a link if necessary (3) Once you correct the slope (1.25-1.185)/720m which is a slightly downward slope and account for the beam spread, and Earth curvature, my estimated height for the lower edge of the beam is 2.1 meters at 6044m out, so just above your board a bit. (4) your image is not sharp enough to answer that -- which direction is the pilot facing at that exact moment? (he keeps turning around to check where the laser is) (5) In image C5 you are clearly using that point as 130cm and put the center of beam at 134cm -- so it doesn't matter if you USED IT for the measurement, you are calling that point 130cm above the water. And then in C11 we get the same reflection off the metal bar, at the same point, and you marked that as 1.84 -- how did the metal bar get higher? (6) It doesn't matter if you think the pixel estimates are wrong or not - it's irrelevant to the actual problem - you haven't shown that your measured heights are reliable. That's all I'm asking for and I've merely shown WHY it is a valid concern. (7) Yes, if you leave in all your methodological errors it doesn't work -- that's the point (8) We've shown how they were done -- you would need to show they are inaccurate by showing how the height was measured accurately. (9) I don't 'believe it' I showed the problems from numerous lines of evidence. (10) See attached image above (11) You misquoted me - I saio "If by change you mean the medium contains components with different refractive indices then yes. " -- all you did was restate what I already said. (12) Please define your term mathematically - then we can discuss further. (13) you cannot estimate refraction as a simple linear function, that's why ATY uses % of curvature as an approximation for the overall integral. (14) you didn't establish they are wrong, you just asserted it - I cited my source, feel free to argue with ATY I have zero interest in discussing irrelevant portions of the calculator any further as I already stated very clearly this has nothing to do with your experiment.

Here is my analysis of the C5 image, the actual, observed, beam spread here is nowhere near 0.08 mRad - whatever you want to attribute the cause, perhaps it's all atmospheric, but it is obviously very large. The spot on the board is almost 70cm across at just 870 meters. That's huge and it gets worse with distance as you clearly see by looking at C2 on up until it's off the board. In C11 you can see it almost covering the whole board but yet, you mark the EXACT SAME specular reflection off the metal bar as the height which you claim is "1.47m" even though it's the EXACT SAME SPOT as in C5 which you called 1.32m in your spreadsheet. How did you get a 15cm rise when the spot on the boat is clearly exactly the same between these two images (C5 and C11)? The smaller spot which you suggested as indicative of the actual beam diameter in C5 is only the specular reflection off the metal bar and doesn't match actual spot size seen clearly in the left side of photo. Every photo past this point only shows the laser reflecting off the patch, metal bar, or camera lens and there are no images that show a tight laser spot on the board but a continuous spreading from C2 onwards. But even though you have only reflections from those 3 spots you continue to mark the "measured beam height" with higher and higher values. Annotated version of C5: I agree that you cannot be 100 percent accurate here but you can get an idea. And remember that the analysis *Mick* was doing NOT looking along the slanted board but looking at it edge on and the marking is nowhere near appearing 130cm above the water. Sure, it COULD be perspective distortions. So let Sandor show how the tape marking was placed and verify it is 130cm above the water. If you watch the video Mick very carefully marks out the top of the tape mark and measures the pixels more accurately than here, this was just the rough swag but it shows what I'm talking about: I don't think it's unreasonable to ask for confirmation of how this specific and critical marking was made to confirm that it wasn't done by placing the tape measure along the slanted angle (but was accurately a measure of that point above the water) when you can very clearly see that do this at two other places in the video - shown below. Since this was their 'slope corrected leveling' mark it determines if the laser is pointing downwards or upwards slightly. An inaccurate measurement at this point renders their overall data inaccurate. Although other methodological errors swamp even this error. And if you reject the pixel counting method then you have to reject all their data past ~C5 because that is all they did - and worse, each of those cases they are counting the pixels to either the reflection off the metal bar, the reflective patch on the jacket, or the camera -- at no point past C5 do they have anything that would mark the actual center of the laser beam. I even showed above where they are calling the exact same reflective spot on the boat as being two different heights.

The horizontal distance the boat travels is very clear in the video. Your white board is 2 meters wide so you can easily mark that width on the video and see the extents showing how far to the left and right the reflective patch and camera lens are showing reflections. You keep denying this is the case but that doesn't make the clear evidence go away. You don't have to debate anything - the information is here for others to evaluate and review. I linked to the evidence showing the photographic analysis showing the 130cm mark is incorrect. The analysis was that the 1m tall board was ~452 pixels (which gives 452 pixels/meter). Total vertical height to the top of tape marked "1.3m" = 536 pixels. This is closer to ~1.186m than 1.3m Sandor Szekely wrote: "On the photos you can tell the height of the laser by calculating the number of pixels above the board and comparing them with the board size. If you use a high resolution photoshop you can calculate quite precisely." Isn't that exactly what you did in all of your photos past about C8? Because you don't have a board even, you have a reflection off a special reflector on one guys coat and off the camera lens and that's it. But you called all of those slightly increasing heights by counting pixels - correct? This is exactly what Mick did and anyone can replicate it as he provided the details in his video. They also estimated that your board was slanted at ~24° and we see the people on the boat repeatedly putting the measuring tape along side the slanted board. This puts your measurements at ~1.3*cos(24°) off -- that's about .91 so that puts you at about 1.188 -- which agrees with the photographic analysis. So there are two data points that suggest this error is real. You can easily refute this -- please show the photo or place in the video where this tape is marked at 1.3m and it was done accurately with the tape measure fairly plumb and not slanted at ~24° along the board. it's that simple really. Maybe we just missed it. But continuing to assert that everything is perfect doesn't make your case. There is very good reason here to believe that this mark was placed incorrectly. That throws everything else about your calculations off. You also did not measure or demonstrate in any sufficient way the beam divergence past about C8 -- and you also have not accounted for the beam divergence in your calculations. Assertions do not make the data reliable. Again - your evidence is only needed if you want to convince others, or you can continue to ignore this -- it's really up to you. I gave the evidence supporting my argument, perhaps that could be addressed? I know that's painful to hear but these are absolutely critical and deep flaws in the methodology and measurements here. As I'm sure you are aware. =========== the rest of this is mostly irrelevant commentary on the aforementioned calculator ================== First of all, NOTHING about the refraction portion here was mentioned in the context of your experiment. I was showing another member that the calculator exists and is very handy and the results matched their numbers which gives us confidence in both. It simply uses a "surveyor standard refraction" as a GUIDE to what one would expect under fairly common conditions (see below). This, in no way, makes it a 'joke'. One must use information appropriately, as always. If by change you mean the medium contains components with different refractive indices then yes. But refraction doesn't require some kind of dynamic 'change' to make it happen. Everything could be entirely stable. In practice it isn't but that's a different store as to what refraction is "DUE to". It is just a tool -- you are free to go write your own refraction calculator. Mick & I have discussed our desire to do exactly that but it is an extremely complex and large project. 7/6*R is very easy and gives you a ballpark/starting point to consider. Perhaps it would be wiser to consider it since every surveyor knows that you must account for refraction when shooting longer sightlines. Note even remotely, it uses 7/6*R (see next bit) It's not really all that 'huge' -- on the horizon, for the Sun, the "average amount of atmospheric refraction" is given as ~34 arcminutes (slightly more than one apparent solar disc). That's going through the entire atmosphere the long way. The calculator uses the approximation given by ATY based on a surveying rule of thumb:

Please note that Mick had emailed the PI of the referenced paper [pdf] who replied as follows:

This image perfectly shows that the laser beam divergence is fairly large as you are clearly getting reflections over several meters wide as the boat slews across the view. These clips are found in the video starting at https://youtu.be/GBhDFO4NMrw?t=1111 (severalbroken clips from that point) and you can clearly see the boat is slewing very much side-to-side, it is not moving straight away from the laser, and you can see these glints across a very wide swath. So all your showing is that a very divergent laser beam is hitting the reflective patch on the back of the white jacket and sometimes glinting off the camera lens pointing back at the dock. These are not accurate measurement methodologies and do not indicate the center of the laser beam. This, combined with the ~10cm error in your 'slope corrected leveling process' mean this experiment does not give us accurate results. Here is my summary with l inks to the main metabunk posts that support them (credit to Mick for the analysis here, I'm just summarizing): 1) measuring height along the slanted board, likely resulting in ~9% error in 'slope corrected leveling' method [link1,link2] - confirmed by observing measuring methodology used and also by photo analysis. This likely resulted in a slight initial downward slope on the laser. 2) laser beam divergence is clearly much greater than they are admitting, creating false hits (shown in #3 & #5) 3) reflective patch on back of jacket and glints off camera lens giving false 'hits' [link1, link2] 4) 'direct hit in camera' is also demonstrated as not reliable (combined with #2 & #3) [link] 5) evidence that the laser is initially pointed slightly down (data at C5 & C8) [link] If these are wrong please post the images that refute them. Here is kind of a guide as to what I think would be needed to address these points... 1) you would need images/video to show that the 130cm marking tape was placed accurately. We can see them using inaccurate methodology (slanted measurements) in other parts of the video but this isn't shown. So you can refute this by showing that the same methodology was not used when placing the 130cm tape mark but that it was made very plumb to the surface of the lake and not made by measuring the distance on the slanted board. 2) you would need to show the laser fully hitting the board at each point past ~C5 showing at least 1/2 extents of the beam divergence. All the evidence I can see past C4 is an increasingly divergent beam. Hits on the reflective tape and lens of the camera do not count to show that the laser divergence is small when we can plainly see in the video that this is not the case (something you seem to have a problem accepting). 3) the reflective patch and camera lens glints are pretty much self explanatory as being invalid. I don't see how you can show otherwise but I'm open to any further evidence presented. 4) 'direct hit on the camera' methodology is just busted - you can see the same effect in the camera even when the laser spot is small on the board in the closer measurements. 5) demonstrating #1 would call this into question depending on the results of that further analysis. But already at C8 we can see the beam is so diverged that it's difficult to see the actual extent of the beam hitting the board. Do you have *anything* that shows the beam extents very clearly past C8 or not? You might appreciate this calculator: https://www.metabunk.org/curve/?d=77&h=3&r=6371&u=m&a=n&fd=60&fp=3264 For 77km and an observer height of 3 meters it gives us the following: Distance = 77 km (77000 m), View Height = 3 meters Radius = 6371 km (6371000 m) Horizon = 6.18 km (6182.72 m) Bulge = 116.33 meters Drop = 465.33 meters Hidden= 393.57 meters With Standard Refraction 7/6*r, radius = 7432.83 km (7432833.33 m) Refracted Horizon = 6.68 km (6678.1 m) Refracted Drop= 398.85 meters Refracted Hidden= 332.65 meters Tilt Angle = 0.692 Degrees, (0.0121 Radians) Horizon Dip Angle = 0.056 Degrees, (0.0010 Radians) Most of these are pretty obvious and the full results explain some of the math used but very quickly... Horizon = distance from observer to horizon point (assuming no obstacles and level ground) Bulge = 116.33 meters -- that's the hump in the middle as you found Drop = 465.33 meters -- the 'drop from a tangent line', as you found Hidden= 393.57 meters -- how much of an object at that distance the observer would be unable to see due to the Bulge blocking the view (again assuming everything is level and no obstacles) These all assume a Spherical Earth approximation but you can tweak the radius at your location if you want (but it only changes the results by micrometers for these smaller distances) Tilt angle is how much an object at that distance would be 'tilted' away from the observer (not very much) Horizon Dip Angle is more for higher elevations and over open waters, but gives the angle down to the horizon assuming no obstacles.

http://aty.sdsu.edu/~aty/explain/atmos_refr/bending.html cites Wegener as 0.114 °K/m (inversion) to match Earth curvature (so any temperature data would need to be very accurate) -- keeping in mind that this would only need to hold for the narrow band where the laser was passing. Standard temp gradient isn't sufficient to prevent light from curving down towards Earth, so it doesn't have to be an inversion to have a significant amount of 'downwards' refraction. I also recommend anyone interested in this 'experiment' and the history to read the Metabunk thread which started before the experiment and has a lot of data following... https://www.metabunk.org/lake-balaton-laser-experiment-to-determine-the-curvature-of-the-earth-if-any.t7780/ Where you'll find that most of the readings were made by the method of 'we can see the laser in the camera' from a moving boat - which we found to not be very reliable since there is clear evidence that this is not sufficient is cited in the metabunk thread. There is no control or measurement for laser beam divergence, which was originally promised to be impossibly fine (0.003 mRad, here) but clearly shows up as much larger through-out the 'experiment'. No controls for refraction, no fine-grained temperature data at or near the level of the laser, no clear data on laser divergence past about 700m, leaning board (correction, likely significant as it impacted the 'leveling' measurements by perhaps 10-11cm), some measurements made from still boat others while moving, inaccurate method for height measurements past the 700m mark (camera hits not established to be reliable), laser too low (they were warned about this repeatedly and ignored it), the photo timestamps and gps data do not align in some cases raising concerns about the data accuracy. They did not take multiple short sightings, they did not have loop closure, error calculation, or use any surveying technology, techniques, or methodology. Most of Sandor's first post here is from the Lake Balaton paper ( http://publik.tuwien.ac.at/files/PubDat_228814.pdf ) which is not his work. They really only have the video and some stills and their table of measurements. My post showing clear evidence of tons of refraction: https://www.metabunk.org/lake-balaton-laser-experiment-to-determine-the-curvature-of-the-earth-if-any.t7780/page-13#post-190072 Post with plot of their Excel data: https://www.metabunk.org/lake-balaton-laser-experiment-to-determine-the-curvature-of-the-earth-if-any.t7780/page-16#post-190250 HOWEVER, their data is interesting -- who knows, maybe the water on this lake is flatter than it should be. Hope this is helpful Update: Mick created two clips showing the beam divergence issue and why hits on the back of the guys jacket reflector and from camera lens do not likely indicate 'center of beam'. This combined with possible measurement error for '130 cm' on the board actually being closer to 1.185cm likely explain a significant portion of the observations.