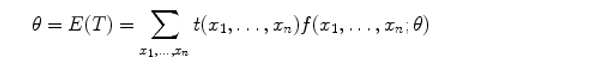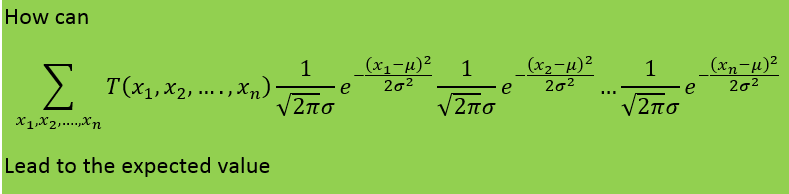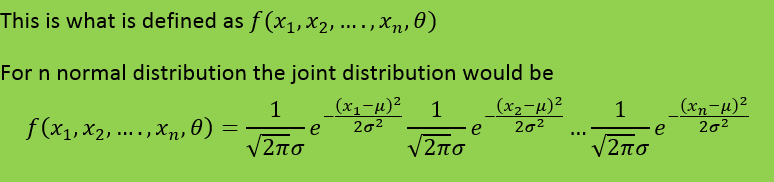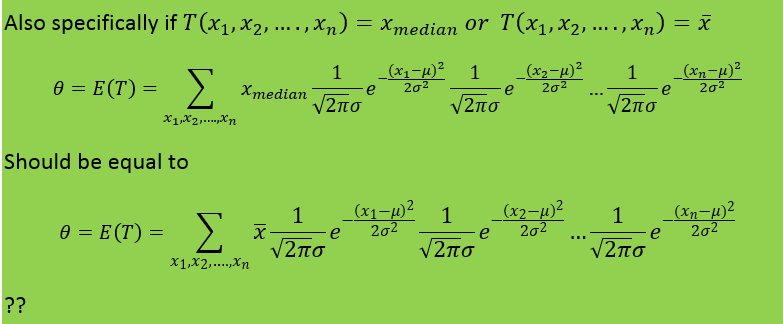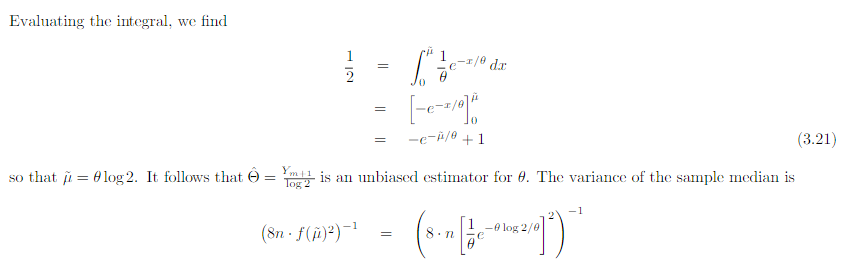Tor Fredrik

It does not have to be a new theorem where E=mc^2 has not been applied. But a quantification of why E=mc^2 is legit. I am pretty sure I read something about it. Could you write a list over all proofs of E=mc^2 that you know? Semi emperical and not emperical. Would be great.

Albert Einstein did introduce E=mc^2 historically. I have seen numerous proofs for this relativisticly or by calculus from Newtons laws. However for some time ago I found a site that described that a scientist did prove E=mc^2 from an energetic perspective by adding together all energy available from different energy types. I can't find this site online now unfortunately. So I wonder if anyone know the name of this proof for E=mc^2 by adding together different energy contributions. I don't want a derivation I simply want a site that describes this theory or the name of the theory if it has one. It is not this wikipedia page I am looking for https://en.wikipedia.org/wiki/Mass–energy_equivalence I believe the proof was introduced a bit later then Einsteins proof perhaps later then 1930. I cant remember if it was semiemperical or not.

So how do you interpretate this. For example for a normal distribution. I have an assignment about this in my textbook It would be easier if someone could show me directly how this is valid

I will add the start of the theory that obtains the fisher information from the maximum likelihood function My notes from this theory is that they talk about the maximum likelihood estimator and that they introduce a sample which should be T in the theory in the first post. My question is still the same: Above they use the expected value of T where T is the estimator for example mean or median as in the example in the beginning of the question. But since they find the expected value of T must not they then use the pdf that corresponds to T? Which in the example above would be gamma and normal respectively. How can then Cramer Rao bound compare anything Just for clarification. The example in the beginning of the first post is not from the rest of the theory. The theory after the example in the first post comes just after this theory added in this post in the chapter of the theory is taken from. Thanks for the answer.

In the example above they use the cramer rao minimum variance estimation. I have one problem. For the mean they use the pdf of exponential. However the mean of exponential follows gamma. And the median distribution can be shown to be normal distributed in general. Why do they use the exponential pdf in Cramer Rao when the mean is gamma distributed? And how can they compare the median and the mean with Cramer Rao when they follow different distributions. I have a derivation in my book of Cramer Rao that starts with mle and uses the pdf until it shows that the covariance between the estimator and the fisher information of the pdf is bounded. But is it not so that you must use the same pdf if you were to compare estimators. This last problem is what I need most clarified. How is it so that Cramer Rao be used if it compares estimators that follow different distributions? In the example above the estimators follow different distributions Thanks in advance! Below I have added how they derive Cramer Rao bound in my book with a comment Above they use the expected value of T where T is the estimator for example mean or median as in the example in the beginning of the question. But since they find the expected value of T must not they then use the pdf that corresponds to T? Which in the example above would be gamma and normal respectively. How can then Cramer Rao bound compare anything if it looks at the bound for different pdfs? Here is the rest of the proof just in case

The theory is taken from this page just in case: http://www.uio.no/studier/emner/matnat/fys/FYS4130/v14/documents/kompendium.pdf

I believe I have made some progress: But in an equilibrium which I want to calculate with an ideal gas approximation. One uses standard chemical potential. Does anyone know how I can find the numerical value of the chemical potential for an ideal gas?

I could come up with one reasoning: Can anyone come up with a bigger picture for why dS_sur is given by -dH/T? I know that dH=dU+pdv+Vdp=dQ-pdV+pdV+Vdp if dp=0 dH=dQ. The problem is why this Q is the Q of the surroundings?

The text above derives gibbs energy to only be a function of entropy. Since I can't get math signs working I have to upload my question in an attachment:

I guess I know that they don't go in circles and are located somewhere around the proton at any time and that their paths for all I know can be one of any route as long it is in the viscinity of the proton. But with that electron probability cloud I have the same question I guess. What force makes the electron fuzz around the electron. One force is the electrical force between the electron and the proton. But that one is more denying the electron to leave and should not give it velocity. What force gives the electron velocity.

I wondered if I could ask about another thing. What causes the circular movement for an electron in a hydrogen. Is it magnetic forces or something else?

I wondered if I could ask about something else: Does the hydrogen electron change spin direction by itself or does it need help from another force? And if it changes by itself. How large is the energy that it emitts as E=hf equal to? I assume that the spin is -0.5 or 0.5 as predicted by stern gerlach.

How strong is the magnetic field that a hydrogen electron experiences from a hydrogen proton when the electron is in s1?

I did get the article. It looked nice. The volume part change of entropy is directly related to disorder. See this article http://www.pa.msu.edu/courses/2005spring/phy215/phy215wk4.pdf The temperature entropy relation to number of states are as far as I can see related to amount of energy in the system, the more energy the more entropy. And the higher number of molecules, the more energy and more enntropy. The temperature side of entropy as I have learned it is related to the boltzman distribution which is one of the main theorems in thermodynamics. You could find a derivation in the litterature.Atkins physical chemistry was were I found the most info about it myself.

It is also possible to rewrite the micro def of entropy S=klnW to the macro def of entropy [math]S=\frac{Q}{T}[/math] both for temperature and volume change. And since S=klnW gives number of combinations that gives the entropy for a given p,V,T it means that the law that max combinations, max entropy (as given in statistical thermodynamic) is most spontaneous can be derived mathematically to the macro version as well. The macro version and calculations are often used in introduction courses in thermodynamics without this derivation. So to me as I look back it seems a bit backward when you take the course that they dont enlighten us with a derivation of entropy from micro to macro mathematically first.

I don't get how they derive (2.18). I get how they derive (2.12) but I don't get what they can do different in (2.8)-(2.12) in order to end up with (2.18)? That is I don't get how they get the term [math]- \gamma F \frac{dp}{dx} [/math] The text is taken from: http://pages.physics.cornell.edu/~sethna/StatMech/EntropyOrderParametersComplexity.pdf