Bob_for_short

IT IS A POLL! I would like to learn if you've ever heard of the positive charge atomic form-factors before my asking this question. The positive charge atomic form-factor fnn'(q) stands at the nucleus charge Z and describes the positive charge cloud in atoms for the elastic (n→n) scattering channel at large angles. It also describes the inelastic scattering channels - "hitting" nucleus by a projectile excites an atom (n→n'): dσn→n'(q)/dΩ ~ |Z⋅fnn'(q) - Fnn'(q)|2 The elastic and inelastic positive charge atomic form-factors are entirely determined with the atomic wave functions ψn(r) and they have nothing in common with the Hofstadter form-factor describing the proper nucleus size. The positive "cloud" size may be very big if the initial and the final atomic states ψn(r) are excited and metastable, like in Rydberg atoms. This is just an effect of the nucleus motion around the atomic center of inertia. Physically it is of the same nature as the negative (electron) charge atomic form-factor Fnn'(q). The numerical difference is just in the "could" sizes - the negative one is larger (~an), the positive is smaller (~(me/Mp)an for Hydrogen, for example). The scattering angles where these form-factors "work" differ essentially - at small and large angles correspondingly. 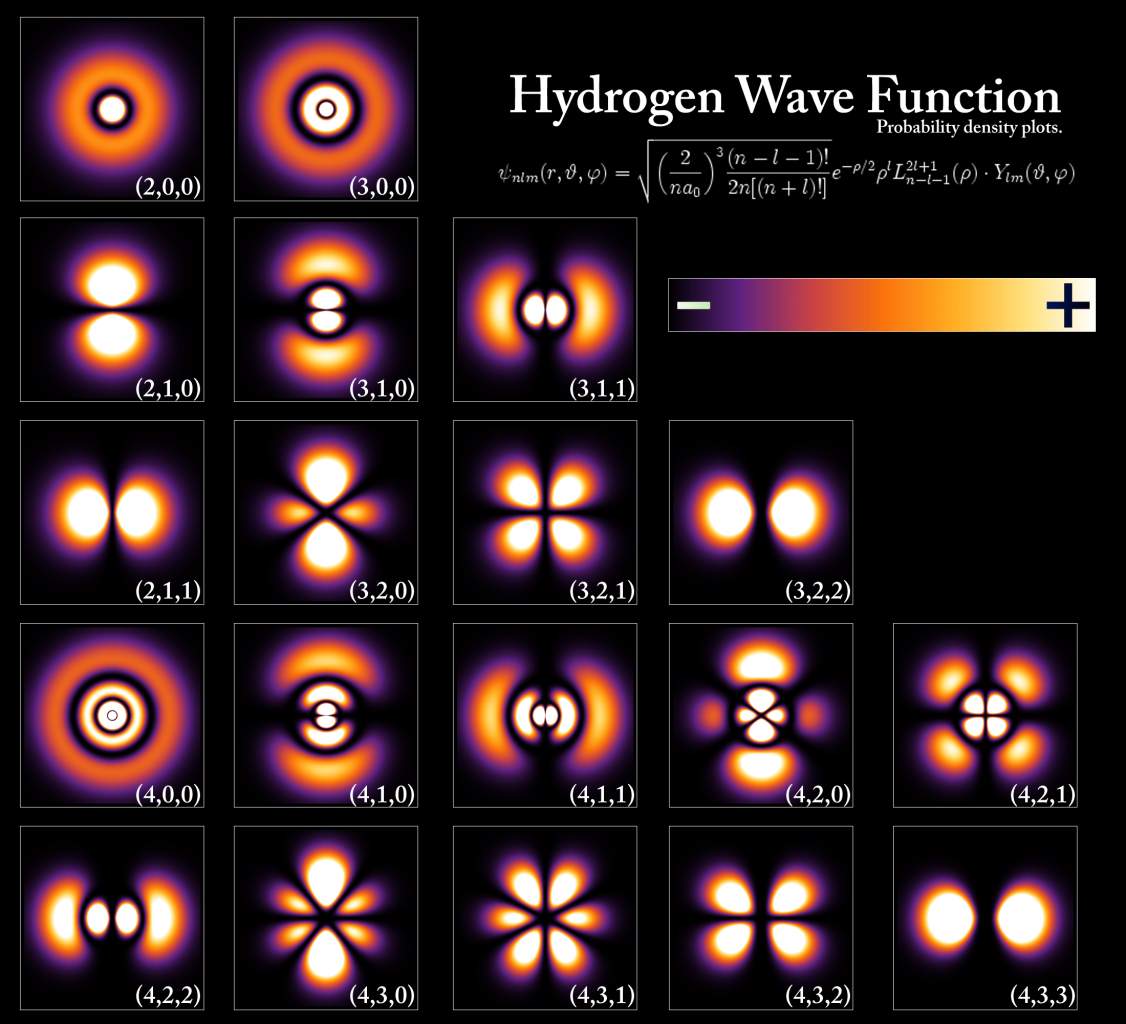The positive charge cloud is simply an atomic nucleus (not nuclear) shell. For Hydrogen atoms it resembles the usual atomic orbitals but at smaller distances (I provide the atomic orbitals in a figure attached). As you can see in the figures, the positive charge is not concentrated at a point but smeared quantum mechanically. Each "separate" sub-cloud carries a "fractional" positive charge, just like a negative sub-cloud. Such pictures resemble sometimes the electric charge distributions in nucleons that normally used as an evidence of quark/parton nucleon structure. The details can be found in my article "Atom as a "dressed" nucleus" in arXiv (http://arxiv.org/abs/0806.2635). The journal version of "Atom..." is available at the Central European Journal of Physics site: http://www.springerlink.com/content/...5b899036dπ=0 Final remark concerning observation of these atomic nucleus shells (it is explained in detail in "Atom..."). Observation is possible in the elastic scattering processes when the initial and the final states of the target atom is the same: ψn(r)→ψn(r). We have to deal with fast charged projectiles whose de Broglie wave-length is smaller than the positive cloud size and we have to scatter them to large angles. In these conditions a fast charged projectile transfers a big momentum q to the nucleus so the atom can get easily excited (inelastic processes dominate: ψn(r)→ψn'(r)). In reality it is difficult, without special experimental facility, to distinguish the elastic from inelastic processes. When one observes only the scattered projectiles, all cross section (of elastic and inelastic events) are added up experimentally. It is called the inclusive cross section. It is easy to show that the inclusive cross section dσinclusive=∑dσn→n' is reduced quite accurately to the Rutherford cross section, as if the target nucleus were "free" and situated at the atomic center of inertia. This fact explains why the notion of point-like particle finds the "experimental" support. In specially designed experiments one can distinguish the elastic dσn→n from inelastic cross sections and obtain the figures presented below. You can also leave your opinion on whether the effect of the positive charge smearing in atoms seems to you as realistic as the negative charge smearing or not. Of course, if you have not studied this subject (scattering from atoms, atomic form-factors), leave the third answer. Do not hesitate to participate and thanks for your answers. Vladimir Kalitvianski.

Let me mention one oversight (many studied, none noticed): the positive charge atomic form-factors. I was really surprised to discover this simple thing myself (1985). It is still unknown to the majority of physicists. You can find details in my article "Atom as a 'Dressed' Nucleus".

Such a precision is explained with a very small value of the expansion parameter (about 0.001). Currently the calculation is made to the forth order so the precision is very high. It is not correct to demand from new theories to overcome this precision - it would take too much effort from one person.

One more article on removing divergent corrections by reformulation of the original problem in better terms: On Perturbation Theory for the Sturm-Liouville Problem with Variable Coefficients by Vladimir Kalitvianski, http://arxiv.org/abs/0906.3504. In this article I study different possibilities of analytically solving the Sturm-Liouville problem with variable coefficients of sufficiently arbitrary behaviour. I obtain correct formulas in case of smooth as well as in case of step-wise (piece-constant) coefficients. I show how the problem can be reformulated in order to eliminate big (or divergent) corrections. I build a simple but very accurate analytical formula for calculating the lowest eigenvalue. I advance also new boundary conditions for obtaining more precise initial approximations. I demonstrate how one can optimize the PT calculation with choosing better initial approximations and thus diminishing the perturbative corrections. The consideration is made on a physical level of rigour. "Renormalizations" or "dressing" are discussed in Appendix 4.

To confirm experimentally these pictures it is necessary to analyse the elastic scattering cross section. It is possible in principle. I think it has already been an object of experimental research. By the way, similar pictures are valid for the positive charge in Hydrogen but they scaled down to much smaller sizes. The atomic nucleus "turns around" the atomic centre of inertia as well as the electron so there are two "clouds" of different sizes and different sign of electric charge (http://arxiv.org/abs/0806.2635). Bob.

In our imagination many things are possible. Most of all we remember the past but we do not know the future. Thinking of the past creates sufficient space and time for our imagination. We "extrapolate" the lasting past to the future. When we film events and watch them again and again (a movie) it is still all about the past. Bob.

It is an experimental fact. We have to recognize it. Classical mechanical example is given in "Reformulation instead of Renormalizations". Of course, you have to keep in mind that the classical picture is the inclusive quantum mechanical one. I hope you are sufficiently educated to understand a simple QM problem outlined in "Atom as a "Dressed" Nucleus". Bob.

For copying-and-pasting π²³ ∞ 0° ~ µ ρ σ ∑ Ω √ ∫ ≤ ≥ ± ∃ … ⋅ θ φ ψ ω Ω α β γ δ ∂ ∆ ∇ ε λ Λ Γ ô

for copying-and-pasting π²³ ∞ 0° ~ µ ρ σ ∑ Ω √ ∫ ≤ ≥ ± ∃ … ⋅ θ φ ψ ω Ω α β γ δ ∂ ∆ ∇ ε λ Λ Γ ô

I hope the prevoius posts have answered your questions. I would like to add that in a dielectric media the light velocity is smaller than c, and there are particles moving in the media with v>c. If such a particle is charged, it emits Cherenkov's radiation (I mean the media+charge both work on radiation). If such a particle is neutral, no radiation is produced. So it can be faster than light. Nothing special. Bob. Merged post follows: Consecutive posts mergedAnother trick: Take a rectangle and launch a fast particle from one corner to the closest side (a short-cut), and launch the light along the rectangle diagonal from the same corner at the same time (a long-way). It is well possible that the particle reaches the opposite side before the light. Bob.

In physics many things resemble accounting: between objects there are exchanges with energy, momentum, angular momentum, for example. Math helps do this bookkeeping, if you like. Bob.

No, SR was not controversial. The problem was in H. Loretnz who knew the works of H. Poincaré on Poincaré's principle of relativity and relativistic mechanics. H. Poincaré in turn considered his own contribution modestly and attributed the main achievements to H. Lorentz. H. Poincaré had written many scientific and popular articles on this subject, and A. Einstein studied them. But A. Einstein never mentioned the works of the academician H. Poincaré and tried not to mention the Lorentz transformations. He popularized the principle of relativity with playing with clocks and rods but he never dealt with real conceptual problems, for example, with radiative friction in relativistic mechanics. His achievements were not so personal. With H. Lorentz alive at that time, it was not possible to give the Nobel prize to A. Einstein for SR. GR was developed also with help of H. Minkowski, M. Grossmann, and D. Hilbert (the latter was still alive). Bob.

Yes, in interactions the particle energy and momentum (as well as the angular momentum) are not conserved but exchanged. The total energy, momentum and the angular momentum of a system may conserve (transferred from one subsystem to another with no change of the sum). Bob.

For me a dead cat does not exist as does not exist a decayed mu-meson. By the way, what does happen to the mu-meson proper reference frame (watch and three space axis X,Y, and Z)? Do they explode together with the mu-meson while decaying? Bob.

The correct question should sound like this: "Does my avatar annoy/distract you while reading the posts?" My answer is "yes". Bob.

A lightwave is easily visualizable in a dusty but nearly transparent medium (foggy atmosphere, for example). Bob.

According to my experience, cats are always alive and funny. I never observed a dead cat in nature. As cats are unpredictable, there is no science describing them. Bob. P.S. They often hide in boxes and other places. Have cat experience from YouTube.

Classical mechanics says where the cat center of inertia is and what the relative coordinates (of tail, paws, head) are. "Dead" or "alive" are not CM notions. In Quantum Mechanics we must be careful and keep in mind the Heisenberg uncertainty principle. In the cat is in a box, the box sizes are involved in HUP The rest is not physics. Bob.

Dear colleagues, In this thread I would like to share with you my findings in the so called renormalization prescription. Very briefly, I managed to reformulate the QED in the way that excludes appearing infrared (IR) and ultraviolet (UV) infinities. As you know, in all renormalizable theories one has to carry out the renormalization procedure. In my opinion, such a prescription is nothing but discarding corrections to the fundamental (phenomenological) constants. This is mathematically unacceptable. By chance it may work, but not obligatorily. In my work (http://arxiv.org/abs/0811.4416) I managed to make this as evident as possible. I reduced the problem to 1D classical mechanical (CM) problem that contains in fact all the elements necessary to understand the “nature” of the renormalizations. You will be surprised to see that even in CM one may obtain corrections to the fundamental constants if its equations are written in the so called mixed variables. The mixed variable formulation is as legitimate as any other formulation if your system is made of a “kit” (can be mounted and dismounted). The mixed variable formulation happens to be wrong physically if your system is “welded” (cannot be dismounted into several parts). The latter is the case of the charge-field interaction. The constant renormalization (= correction discarding) is not legitimate mathematically. It is only a good luck that this “works” in some cases. I tried to simplify the problem as much as possible to exclude any doubts and leave the essence apparent. That is why my paper deals mostly with CM problem. I hope the understanding achieved in this work (as well as in http://arxiv.org/abs/0806.2635) will permit to reformulate the particle theories in a more natural way, free from infinities accompanied with wrong justifications in their “doctoring”. We have to recognize that the massive particles and massless fields do not exist separately even in the zeroth approximation but form compound systems. Their QM description is much similar to the QM atomic description: via the center of inertia and relative coordinates. In particular, the electron and the quantized electromagnetic field form an “electronium” where the internal degrees of freedom are described with the photon oscillators. The charge in such a compound system is quantum mechanically smeared (not point-like), just as the negative and positive charges in an atom. This construction leads to much more physical initial approximation of interacting particles and to the sensible results of calculations without appealing to a “shell game”. There is no correction “doctoring” in such an approach. It describes the known QED effects in a natural way. The “free” charge scattering is obligatory inelastic. The inclusive picture (cross section) corresponds to the experimental observations. I invite the researchers to read my simple paper and make remarks if any. Sincerely yours, Bob. Atom_CEJP.pdf Reformulation_instead_of_renormalizations.pdf

Indeed, a single travelling photon is a wave packet or a wave train. It contains many wave-lengths (10000-100000, it depends). If you catch a photon between mirrors, it can become a standing wave, again, of finite length. Bob.