Rob McEachern

I specifically stated the condition "If your friend actually answers" - so getting through to only someone else is no longer even a possibility.

Not when you get EXACTLY what you expect. Think about dialing a friend's phone number. If your friend actually answers, do you report that there is some remaining uncertainty about having actually dialed the correct number, or some uncertainty that the telephone system may have not correctly connected your call? Of course not, because the mere act of your friend answering (your expectation has been perfectly met), confirms that fact that there was no uncertainty, in that particular experience.

Exactly the problem, and the subject of this thread. Uncertainty of what? That is the question. If you always experience exactly what you expected, then you are unlikely to say there is anything uncertain about that experience. So uncertainty is a function of expectations (think allowed symbols, in the above posts). So if you expect the measurements to behave one way and they actually behave a different way, then there are several possible alternative causes for the difference. One is that there is something wrong with the measurements (corrupted by noise) as you have stated. But another is that there is something wrong with your expectations - your a priori model of the way things are supposed to turn out. If you expect to be able to measure two or more independent variables, where only one actually exists, then the correlations between your measurements will be unexpected (and thus proclaimed to be weird), but not due to being uncertain. See my post here: link removed by moderator

Note the timing of my edit, in which I corrected your name, before your post. So much indeed. Noise on the input has been totally eliminated from the output, not merely reduced. The claim pertains to the output, not the input. It is directly relevant to the interpretations (decisions) being made in physics. For example, if you think the allowed states of a Bell polarization state measurement must always be either 1 or -1, but 0 (zero) is also a rare, but allowed state (like viewing a coin edge-on), you will end up with some rather weird interpretations of the measurement correlation statistics, which is exactly what has happened.

Swansont's replies are incorrect. The reason, though subtle, is of vital importance to all sophisticated communications systems. Koti specifically noted "when a system acts..." Swanson misinterpreted "act" as "measure", but all sophisticated communication systems do much more than just make measurements - they make decisions based upon their measurements; and the entire point of making those decisions is to COMPLETELY eliminate the noise from the decision output sequences. This is done by exploiting a priori known limitations on ALLOWED measurable states. Think of the English alphabet; there are only 26 allowed letters (symbols). Consequently, if a system (such as your brain) receives a letter that is so noisy that it does not appear to be one of the allowed letters, it will detect that error and take steps to correct it. As a simple example, sequences of letters spell words (super symbols); a crude spell-checker can simply compare each received super-symbol (word) to a dictionary of all ALLOWED words, detect unallowed words and then substitute the closet matching allowed word, to correct most noise-induced errors. More sophisticated systems can create super-super-symbols, as allowed sequences (grammatically correct) of multiple words, to further reduce the number of errors in the decision sequences. This is why your HD television picture is so much cleaner than an old analog TV picture. The analog TV merely measures the input voltage, as Swansont has assumed, and paints the screen with it, received noise and all. But an HDTV system transmits easily recognizable sequences of allowable symbols, that enable gargled symbols to be detected and completely replaced by clean ones. This does not merely reduce the noise, it entirely eliminates it, under most circumstances. When the system is unable to correct the measurement errors, the result is usually a catastrophic failure - the created picture, if there even is one (most HDTVs will blank the screen if the reconstruction is too bad), is highly distorted, like pieces of a jig-saw puzzle that has been assembled incorrectly.

The problem with this theorem, Bell's Theorem and all similar theorems, results directly from the assumptions stated on the top of page 4, in the paper that you cited: " the “macro-realism” intended by Leggett and Garg, as well as many subsequent authors, can be made precise in a reasonable way with the definition: “A macroscopically observable property with two or more distinguishable values available to it will at all times determinately possess one or other of those values.” [8] Throughout this paper, “distinguishable” will be taken to mean “in principle perfectly distinguishable by a single measurement in the noiseless case". " The first problem is, that some "macroscopically observable properties", may only ever have one value to it, zero, at all times, in "the noiseless case". Thus, it violates the assumption of "two or more" in the above definition. The second problem is, that all these theorems assume that there is such a thing as a physical state that exists in "the noiseless case." That need not be true - noise may be intrinsic to the physical state of the object being measured. In other words, so-called identical particles may only be identical, down to a certain number of identical bits of information, but no more. Strange interpretations, like Bell's, will result whenever that number of bits happens to equal one, because the theorems have, in effect, all assumed that it must always be greater than one. This is ultimately what Heisenberg's Uncertainty Principle is all about. To visualize these problems, look at the first polarized coin image, labelled "a", in this figure: http://www.scienceforums.net/topic/105862-any-anomalies-in-bells-inequality-data/?tab=comments#comment-1002938 If the one-time-pad is rotated by either 90 or -90 degrees, in an attempt to measure a horizontal polarization component, then the measured polarization will be identically zero, not +1 or -1. In other words, this object has a vertical polarization state, but not a horizontal one. If noise is present, then any nonzero, horizontal, polarization measurement will be caused entirely by the noise: that is, measurements of the supposed horizontal components of the supposed, perfectly, identical particles, will yield differing, random results, whose statistics will appear "weird" to anyone attempting to interpret them as being due to a system that actually obeys the assumptions in the above citation. Note also that when other polarization angles, between 0 and 90 degrees are measured, the results are simply caused by the "cross talk" response of the detector to the vertical component (and the noise) - there is never any response to a supposed, horizontal component, because that component is identically zero, in "the noiseless case" and consequently never exhibits any response. Theorems that assume otherwise, fail to correctly describe reality. That has lead to a lot of "weird" interpretations of quantum experimental results.

No. If the stock loses value, the sell price may never exceed the buy price. On the other hand, the broker fees depend upon both which broker you use (full-service or discount) and the value of the order. Large orders through a discount broker may involve combined fees (buy+sell) totaling only a small fraction of 1% of the total transaction value. Consequently, in high-volume, high-volatility day-trading, such small fees can often be recovered in a fraction of a second, by exploiting the very small trade-by-trade fluctuations in the market price. Exploiting this fact, is what high-speed, computerized trading is all about.

However, it is exactly like observing an entangled pair of polarized coins, rather than a pair of gloves. This has been extensively discussed on the thread http://www.scienceforums.net/topic/105862-any-anomalies-in-bells-inequality-data/?tab=comments#comment-999458 The post I made on July 1, which discusses gloves, socks, coins and all the rest of it. Gloves do not exhibit "quantum correlations", since, as Swansort has stated, they are always in a fixed state of being either right or left handed, INDEPENDENT of any observation. But coins are not in any such fixed state - their observed state DEPENDS upon the observer's decision to observe the coin from a specific angle; change the observation angle and you change the result. Consequently, coins will exhibit the exact same correlation statistics, with the exact same detection efficiencies, observed in the best Bell tests on polarized photons, when the coins are specifically constructed to exhibit only a single bit of information. It is the number of recoverable bits of information (one vs. more than one) that determines the correlation statistics (and the Heisenberg Uncertainty Principle). It has nothing to do with spooky action at a distance, or classical vs. quantum physical objects. See my paper "A Classical System for Producing Quantum Correlations" for details: http://vixra.org/pdf/1609.0129v1.pdf

You might find my unfinished slideshow "What went wrong with the “interpretation” of Quantum Theory?" ( http://vixra.org/pdf/1707.0162v1.pdf ) to be of interest, in answer to your questions. The central points are: (1) De Broglie introduced superpositions into classical mechanics, to enable Fourier transform based descriptions of "tracking wave packets", attached to every particle. (2) The Schrodinger equation is a purely mathematical, Fourier transform based description of motion - it is pure math, not physics; no laws of physics are involved in its derivation. It merely describes the motion of the tracking wave packet, attached to each particle. (3) The double slits can be interpreted as particles scattering off a rippled field within the slits, rather than as any sort of wave interference phenomenon behind the slits. (4) Unlike classical scattering, the limited information content of a quantum system (corresponding to a single bit of information) means that the particle and field cannot even detect the existence of each other (and thus cannot interact with each other) except at the few specific points in which it is possible for a particle to detect/recover at least one bit of information from the field. This is the explanation for the behavior described in David Bohm's 1951 book, concerning the discontinuous versus continuous deflection of a particle in a quantum field versus a classical field respectively.

Tim88 said: "it is based on plausible looking assumptions" Exactly: The very assumption, pointed out by Bernard d 'Espagnat in 1979, that I mentioned in an earlier post. An assumption that has now been demonstrated to be false: It is not possible to measure independent, uncorrelated, attribute-values, when objects (like coins) are constructed in such a fashion, that independent attributes do not even exist.

The second line from your OP was "what was the frequency for Alice and Bob choosing the same test?" The answer is entirely dependent on how many different polarity test settings, have been decided upon. For example, in the paper cited above, 360 settings have been decided upon. So, if Alice randomly selects one test setting, the probability that Bob will randomly select the same test setting, for any one particular test, is 1/360 = 0.278% Because it is very time-consuming to test large numbers of different settings, most experiments use a much smaller number of settings, choosing only those at which the difference between the classical and quantum curves are most significant. A triangular distribution, arises from the fact that the autocorrelation ( https://en.wikipedia.org/wiki/Autocorrelation ) of a uniform distribution (the distribution of both the test settings and the object polarizations) is a triangular distribution.

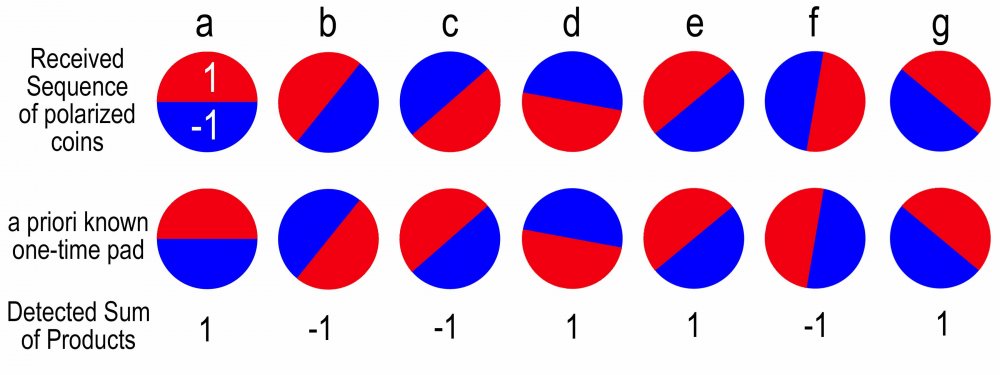
The figure below depicts the fundamental problem with all Bell tests. Imagine you have received a message, in the form of a sequence of polarized coins, as shown in the top line of the figure below. Your task is to decode this message, by determining the bit-value (either 1 or -1) of each coin (a-g). If you know, a priori, the one-time pad (https://en.wikipedia.org/wiki/One-time_pad ) that must be used for the correct decoding (the second line in the figure), then you can correctly decode the message, by simply performing a pixel-by-pixel multiplication of each received coin and the corresponding coin in the one-time pad, and sum all those product-pixels, to determine if the result is either positive (1) or negative (-1) as in the third line of the figure. (Red = +1, Blue = -1). But what happens if the coins are "noisy" and you do not know the one-time pad, so you use randomly phased (randomly rotated polarity) coins instead of the correct one-time pad? You get a bunch of erroneous bit-values, particularly when the received coin's polarity and its "pad" are orthogonal and thus cancel out (sum to zero). But the noise does not cancel out, so in those cases, you end up with just random values, due to the noise. The statistics of these randomized bit-errors is what is being mistaken, for "quantum correlations" and spooky action at a distance.

It is worth pointing-out, that a classical coin, as described above, is simultaneously BOTH a heads and a tails - that is what a superposition of two states looks like - a coin - until an observer makes a decision, and "calls it" - either a heads or a tails. Perhaps it should be called Schrödinger's coin.

“We know the following…” No we do not. We do not even know if there is such a thing as BOTH a spin A and a spin B. You seem to be unclear on what a Bell test is all about, so let me explain. To start with, consider three types of classical objects, a pair of balls (white and black) a pair of gloves (right and left handed) and a pair of coins. If one of the balls, gloves and coins is given to Alice and the other, from each pair, is given to Bob, then both Alice and Bob will instantly know the color of the other’s ball and the handedness of the other’s glove (assuming they were told beforehand, that the paired balls are always white and black, and that the paired gloves are always right and left handed), regardless of how far apart they are; no “spooky action at a distance.” But they will not know the other’s coin state (or even their own!), because that state, unlike the color of the balls and the handedness of the gloves, is not an attribute of the object itself. Rather, it is an attribute of the relative, geometric relationship, between the observer and the coin; when they look at the coin from one aspect angle, they observe it as being in the state “heads”, but when they look at it from the opposite angle, they observe the state “tails”. So before they can even determine the state of their own coin, they have to make a decision, about which angle to observe the coin from. Making this decision and observing the result, is what is mistakenly called a “collapse of the wave-function”. But there is no wave-function, there is only a decision-making process, for determining which state, of several possible, states, the object is in, relative to the observer. Unlike the balls and gloves, objects like coins are not in ANY state, until an observer “makes it so.” Note also that even after the decision is made, the two-sided coin did not mysteriously “collapse” into a one-side coin. There is no physical collapse, there is only an interpretational collapse - a decision. But suppose that the coins were so tiny and delicate, that the mere act of observing one, totally altered its state - it gets “flipped” every time you observe it. Now it becomes impossible to ever repeat any observation of any coin’s relative state. So it is impossible to make a second measurement of such a coin’s original state. This brings us to the EPR paradox. Since it is now impossible to remeasure any coin, as when attempting to measure a second “component”, EPR suggested, in effect, to create pairs of coins that were “entangled”, such that they are always known, a priori, to be either parallel or anti-parallel. Hence, a measurement of one coin, should not perturb the measurement of the other. The relative orientation of the coins, relative to any observer, is assumed to be completely random. But relative to each other, the coins are either parallel or anti-parallel. It turns out that for small particles like electrons, it is much easier to create entangled-pairs that are anti-parallel, than parallel, so we will restrict the following discussion to the anti-parallel case. Now, whenever Alice and Bob measure each coin (one from each anti-parallel, entangled-pair) in a sequence of coins, they obtain a random sequence of “heads” or “tails”, since, regardless of what angles they decide to observe a coin from, all the coins are in different, random orientations. But what happens if they record both their individually, decided measurement angles and the resulting, observed states of their respective coins, and subsequently get together and compare their results? As expected, whenever they had both, by chance, decided to observe their entangled-coins from the same direction, they observe that their results are always anti-parallel; if one observed “heads”, then the other observed “tails.” And if they had both, by chance, decided to observe their entangled-coins from exactly opposite directions, they observe that their results are always parallel. But what happens when they, by chance, happened to observe their coins at other angles? This is where things start to get interesting - and subject to mis-interpretation! Because what happens, is critically dependent upon how accurately Alice and Bob can actually decide upon the observed state of their respective coins. If both observers can clearly observe their coins, and make no errors in their decisions, even when the coins are perfectly “edge-on”, then you get one result (Figure 1, in this paper: http://vixra.org/pdf/1609.0129v1.pdf ) , when the observers get together and compute the correlations between their observations. But if the coins are worn-down, dirty and bent-out of shape, and can only be observed, for a brief instant, far away, and in the dark, through a telescope (AKA with limited bandwidth, duration, and signal-to-noise ratio). Then a completely different type of correlation will appear, due to the fact that many of the observer’s decisions are erroneous; they mistakenly decided to call the coin a “head” when it was really a “tail” or vice-versa. Or they may even totally fail to detect the existence of some of the coins (fail to make any decision), as the coins whiz past them, never to be seen again. And if they attempt to mitigate these “bit-errors”, by attempting to assess the quality of their observations, and eliminating all those measurements of the worst quality, then they will get yet another correlation - one that perfectly matches the so-called “quantum correlations”, when analogous, Bell-type experiments, are performed on subatomic particles, like photons or electrons. So, should quantum correlations be interpreted as a “spooky action at a distance”, or just a misunderstood classical phenomenon? Given the (little known) fact that the limiting case of the Heisenberg Uncertainty Principle can be shown to (just an amazing coincidence !!!???) correspond to a single-bit-of-information being present, which thereby guarantees that every set of multiple observations must be “strangely correlated”, “spooky action at a distance” seems to be an implausible interpretation, at best.

Here is another point that ought to be considered, in the context of Anomalies in Bell's theorem and the related experiments. It is well known ( https://en.wikipedia.org/wiki/No-communication_theorem ) , that measurements of the second member of each pair of entangled particles, convey no information. But what on earth, does it even mean, to make a "measurement" that is entirely DEVOID of any information? If you go back and attempt to understand what Shannon's Information Theory is all about, you will begin to see the fundamental problem, with the whole Bell type argument; which amounts to trying to figure out the meaning, of meaningless (devoid of ANY information) measurements. And this gets back to the assumption pointed out above (Post #10), in the article by Bernard d 'Espagnat; a measurement, devoid of information, which "is converted by this argument into an attribute of the particle itself."; Presumably an attribute, which is also devoid of information.

For some reason, the link in my 20 May 2017 - 08:38 PM post, no longer works. Here is the link, to the Foundational Questions Institute topic site: http://fqxi.org/community/forum/topic/2929

Mordred: There seems to be some gaps in your study/knowledge of QFT. The "L" shaped model, with attached strings, that I mentioned, is not some abstract mathematical entity in string theory. It is an easily observable, real object; a piece of cardboard cut into the shape of an “L”, with three real pieces of string attached to it. Take the cardboard “L” and place it on a table in front of you. Fasten (tape) one end of each string to each of the L’s three vertices. Fasten (tape) the other end of each string to the table top, leaving some slack in the strings. Now rotate the L 360 degrees about its long axis; the two strings attached to the bottom of the L become twisted together (entangled) in such a manner that they cannot be disentangled without either another rotation or unfastening the strings. However, if you rotate the L through another 360 degrees, for a total rotation of 720 degrees, it is possible to disentangle the strings, without any additional rotation or unfastening of the strings; thus the 720 rotation is topologically equivalent to a zero rotation. The device is a variation of the well-known “Plate Trick” AKA “Dirac’s Belt” see: https://en.wikipedia.org/wiki/Plate_trick http://www.mathpages.com/home/kmath619/kmath619.htm In regards to your comment “PS all your arguments have been based upon metaphysical arguments”, the simulation presented in the vixra.org paper is hardly metaphysical in nature. It is a concrete demonstration of an anomalous (AKA false) prediction in the Quantum Theory associated with Bell-type experiments. That theory predicts that no classical model can reproduce the observed “quantum correlations”, while simultaneously achieving detection efficiencies as high as that exhibited in the model. That claim has been falsified: and without even attempting to maximize the model’s efficiency. PS: I’m surprised that you, being a frequent poster on this site, have introduced so many things, that have little or no relevance to the topic of this particular thread. I respectfully suggest you stick to the topic. The model presented, is a direct response to the third bullet in the original post: “Have tests of analogous classical systems been used as a control? such as for what kind of variance to expect?” The model was designed to be directly analogous to the polarization measurements, performed on entangled photon-pairs. That is not a metaphysical speculation. It is a statement of fact.

"Why does it take a 720 degree angular momentum (Spin) to reach the original quantum state while under a spin 1 particle only 360 degrees under the corpuscular view?" For the same reason a simple, macroscopic, "L" shaped model, with attached strings needs to be rotated 720 degrees to disentangle the strings (return to zero). Have you never seen this model? It has been used to illustrate this very point, in discussions of spin, for many decades. It is a property of the geometry and has nothin to do with any supposed wave-functions.

"It is measurable support that the math describes." No. The math only describes the observations themselves, not the causal mechanism (AKA interpretation) responsible for producing those observations. In other words, it provides no "support" whatsoever, for any interpretation. That is the origin of the well-known advice to physicists to "Shut-up and calculate." "Physics doesn't define reality, we leave that in the hands of Philosophers." Nonsense. What do you suppose "interpretations" are? All interpretations of theory, are nothing more than metaphysical (AKA philosophical) speculations, regarding the unobserved and hence unknown causes, for the known effects, called observables. There is no wave-particle duality, outside of metaphysical interpretations. There are only observed phenomenon, like correlations and supposed interference patterns. But mathematically, even the classical pattern, produced by macroscopic bullets passing through slits, is mathematically described as a superposition and thus an interference pattern; the pattern just does not happen to exhibit any "side-lobes". These patterns have almost nothing to do with physics, either quantum or classical. It is simply the Fourier Transform of the slit's geometry. Don't take my word for it - calculate it for yourself. In other words, the pattern is the property of the initial conditions, the slit geometry (the information content within the pattern is entirely contained with the geometry of the slits). It does no matter if the things passing through the slits are particles or waves. Physicists have made the same mistake that people watching a ventriloquist act, when they assume the information content being observed, is coming from (is a property of) the dummy (the particles and waves striking the slits). It is not, as computing the Fourier transform will demonstrate. quod erat demonstrandum The particles and/or waves merely act as carriers, analogous to a radio-frequency carrier, which is spatially modulated with the information content ORIGINATING within the slits, not the entities passing through the slits. Do you assume that the information content of your mother's face, encoded into the light scattering off her face and into your optical detectors (AKA eyes) originated within the sun? Of course not. It was modulated onto the reflected light, regardless of whether or not you believe that the light consists of particles, waves, or a wave-particle duality. The patterns are CAUSED by properties of the scattering geometry, not the properties of the entities being scattered; change the geometry and you change the observed pattern. "It can be measured therefore it does" No one has ever measured an interpretation. "Hypotheses non fingo", was how Issac Newton wisely put it: "I have not as yet been able to discover the reason for these properties of gravity from phenomena, and I do not feign hypotheses. For whatever is not deduced from the phenomena must be called a hypothesis; and hypotheses, whether metaphysical or physical, or based on occult qualities, or mechanical, have no place in experimental philosophy."

What makes you assume that there even is another component, capable of being measured? This is a very old, but very seldom discussed problem, with all Bell-type theorems. If there is only one component (corresponding to one bit of information), then there is no other, uncorrelated component, to ever be measured. See for example this (https://www.scientificamerican.com/media/pdf/197911_0158.pdf) 1979 article by Bernard d 'Espagnat, page 166: "These conclusions require a subtle but important extension of the mean­ing assigned to a notation such as A+. Whereas previously A+ was merely one possible outcome of a measurement made on a particle, it is converted by this argument into an attribute of the particle itself." In other words, to put it bluntly, simply because it is possible to make multiple measurements, does not ENSURE that those measurements are being made on uncorrelated attributes/properties. One has to ASSUME (AKA converted by this argument), with no justification whatsoever, that those measurements can be placed into a one-to-one correspondence with multiple, INDEPENDENT attributes/components of a particle (such as multiple, independent, spin components), in order for the theorem to be valid. But some entities, like single bits of information, render all such assumptions false - they do no have multiple components. Hence, all measurements made on such an entity, will be "strangely correlated", and as the vixra paper demonstrates, the resulting correlations are identical to the supposed quantum correlations. There is nothing speculative about that. It is a demonstrated fact - quod erat demonstrandum. Math that accurately models physical reality does not imply that one's INTERPRETATION of that math is either correct or even relevant to that reality. Both sides of a mathematical identity, such as a(b+c)=ab+ac, yield IDENTICAL mathematical results, to compare to observations. But they are not physically identical - one side has twice as many physical multipliers as the other. The Fourier transforms at the heart of quantum theory, have wildly different physical interpretations, than the one employed within all of the well-known interpretations of quantum theory. All of the weirdness arises from picking the wrong physical interpretation - picking the wrong side of a math identity, as the one and only one to ever be interpreted. All detection phenomenon are naturally incomplete; it is simply a question of how incomplete. Quantum Theory is unitary, precisely because it only mathematically models the output of the detection process, not the inputs to that process. In the case of quantum correlations, only the detections are counted and normalized by that count - the number of detections (not the number of input pairs) is the denominator in the equation for computing the correlation. Think of it this way - if you counted the vast majority of particles that strike a double slit apparatus and thus NEVER get detected on the other side of the slits, the so-called interference pattern could never sum to a unitary value of 1, corresponding to 100% probability. It sums to a unitary value, precisely because the math only models the detections. Assuming otherwise is a bad assumption that has confused physicists for decades. A particle has no waveform. Only the mathematical description of the particle's detectable attributes, is a waveform. But descriptions of things and the things themselves are not the same: math identities do not imply physical identities. Assuming that they do, is the problem. The HUP, is mathematically identical to the statement that the information content of ANY observable entity >= 1 bit of information. But what happens if it is precisely equal to one, and someone tries to make multiple measurements of the thing? Answer: You get quantum correlations. You have missed the point entirely about detection efficiencies. The point is the calculated, theoretical limits for the supposed, required efficiencies, needed to guarantee that no classical model can reproduce the results, have been falsified. Hence there is something very wrong with the premises upon which those theories are founded.

"Superposition being a statistical probability function" Superposition is a mathematical technique that has nothing whatsoever to do with probability or physical reality. It has to do with being able to process one sinusoid at a time, through a differential equation, in order to combine the solutions with the multiple sinusoidal inputs, into a single solution, corresponding to a general, non-sinusoidal input. Mistaking the mathematical model of a superposition, for a physical model of reality, is one of the biggest mistakes ever made by physicists, and the subject of an unending debate. The Born Rule for treating the square of a wavefunction (Fourier transform) as a probability estimate, arises entirely out the little-known fact, that the computation is mathematical IDENTICAL to the description of a histogram process; and histograms yield probability estimates. It has nothing to do with physics. It is pure math.

The biggest anomaly has to do with detector efficiency. It has been known for decades, that classical systems can perfectly duplicate the so-called "Quantum Correlations", at low detection efficiencies; as when only a small fraction of the particle-pairs flowing into the experimental apparatus, are actually detected. Hence, the key question, for all experimental Bell-type tests, becomes, "How great must the detector efficiency be, in order to rule out all possible classical causes, for the observed correlations?" Depending on the nature of the test, various theoretical claims have been made, that detector efficiencies ranging from 2/3 up to about 85% are sufficient to rule-out all possible classical causes. However, a classical system with a pair-detection efficiency of 72%, corresponding the a conditional detection efficiency of sqrt(0.72) = 85% (the figure of merit being reported in almost all experimental tests) has recently been demonstrated (see the discuss at http://fqxi.org/community/forum/topic/2929),and an argument has been made that strongly suggests that 90% efficient, classical systems, ought to be able to perfectly reproduce the observed correlations. Since no experimental tests have ever been conducted at such high efficiencies, the conclusion is, that fifty years of experimental attempts to prove that no classical system can produce the observed correlations, have failed to prove any such thing. Furthermore, the mechanism exploited for classically reproducing the correlations, at high efficiencies, suggests that the physics community has a profound misunderstanding of the nature of information, as the term is used within Shannon's information Theory, and that almost all of the supposed weirdness in the interpretations of quantum theory, are the direct result of this misunderstanding.