Cristiano

You're right (but I need 2*pi because my original n is in revolution/day). What about da/dt= -2 * 10096.676 / n3 * dn/dt / (3 * a2) ?

I know a, n and dn/dt. a3= 10096.676 / n2. I need to calculate da/dt. 398600.8 has unit km3/s2, n is rad/s, dn/dt is rad/s2. EDIT: Probably I'm wrong in the unit of measurement of da/dt; I thought it was km/s2, but it should be km/s, right?

The original formula is a3 = 398600.8 / (2 * pi * n)2 With dn/dt= 6.07340239 * 10-12 rad/s2 I get da/dt= -1.51970883 * 10-5 km/s2 which is -113445.6 km/day2, while I expect about -1 to -10 km/day2.

If I put the real numbers, I get a wrong result. Could you please confirm that the formula is correct?

I know the value of dn/dt (e.g. dn/dt = 123). a3 = 345 / n2 Is there any way to calculate da/dt?

I meant a recursive formula like: a = A/U * (a + b) (I wrote just an example for clarification).

Supposing that I correctly calculate the integral to obtain the circumference and the area (I'm not sure right now), is there any numerical method that I can try? EDIT: I used the formula C= pi * (a + b) [ 1 + sum... to calculate the circumference and my above result (145485.418131498) is good, while the area is wrong.

I know that the area of an ellipse is 1403761773.43497 and its circumference is 145485.418131498. Is there any way to calculate from those numbers that the semi-major axis is 26534.9039306654?

Thank you all. I've never heard of absement, but unfortunately it doesn't seem useful for my problem, which is related to astronomy. I need to calculate the mean radius vector of an Earth's artificial satellite. But probably this is not the right forum. I first need to ask some basic questions about the ellipse... I switch to the math subforum.

If I integrate the speed I obtain the space, but if I integrate the space, what do I get?

I still have a little doubt. We have: v0 = v v' = f(t, v), v= RK(v') b' = f(v, b) When I wrote RK for b', should I first calculate the new v and use this new v as the input for b' or should I use v0, the v before the update v= RK(v')?

Ah! Ok. The same that I do for the n-body simulation. Now it's clear. Thank you very much.

I have 3 variables: v, b and h. I know how to calculate v’, b’ and h’. Starting the simulation from an initial condition, I need to calculate v, b and h after a given time using a numerical integrator (say RK4). If I use the simple Euler method, I write; v= v + dt * v’ b= b + dt * b’ h= h + dt * h’ but when I switch to RK4, I don’t know what to write. The simulation is explained here: https://mintoc.de/index.php?title=Gravity_Turn_Maneuver For example, h’= v * cos(b) doesn’t seem a differential equation; does it mean that h= h + dt * h’ is correct and that there is no reason to use RK4? Also, the second RK4 step is: k2 = f(x + dx / 2, y + k1 / 2) and we have that m’ = constant, v’= f(v, m). When I write the above k2 f(x, y) function, I suppose that I need to consider also m at time x + dx / 2, not only v, in other words f(x, y) is: m = m_initial – m’ * x v’ = f(m, v) and not only v’ = f(v).

Probably the best answer I can get comes from an orbital mechanics book, where it is said that for an (unperturbed) elliptical orbit, the conservation of energy may be written: V2 / 2 = mu / r - mu / (2 * a)

While I'm very thankful for your explanations and for your patience, I still don't see a clear cause-and-effect rule. Probably I should find something that links the kinetic energy with the potential energy for the orbital motion…

There is no doubt that the atmospheric drag is the major cause of the loss of altitude. My point is that the atmospheric drag is a force acting opposite to the motion of the satellite; it seems a paradox to me that the drag accelerates the satellite. There is no doubt that that's true, but how that can be explained?

I agree on your first and last phrases, but in my understanding, the drag is a force that decelerate the satellite, hence the satellite should slow down. It seems no longer available.

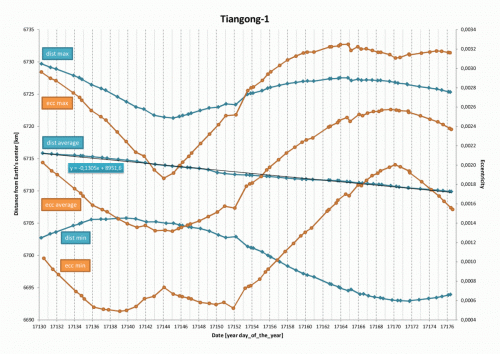
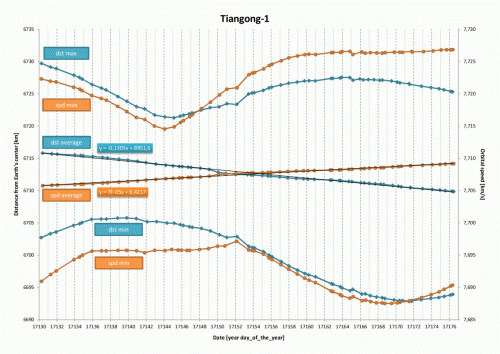
I change my question. The POS/VEL graph (the one on the right) shows that the mean orbital speed is increasing as the mean altitude is decreasing, while I thought that the speed decreases because of the atmospheric drag and as a result the satellite falls to Earth. Please, could someone explain?

I wrote a program to simulate the Tiangong-1 reentry. To better understand how its orbit is changing, I created the attached graphs using 62 TLEs. For each TLE, I calculate the satellite's position, speed and eccentricity by mean of the SGP4 propagator. I collect those values for 5 orbits starting from the TLE epoch with a step of 0.5 s. The "ecc min" and "spd min" behavior seem strange to me in the left half. Is there any chance that the engines (main or RCS) was accidentally fired (I mean a malfunction)?