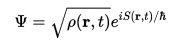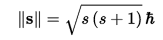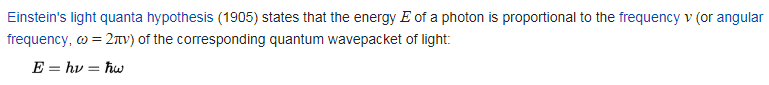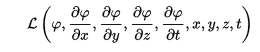Vmedvil

Meh, it is not like anyone is ever going to read this anyways.

Sorry, but it is a quote from something I wanted to use. This definitely debunks a "Fine Tuned Universe"

You know how I said punch a wall and stuff..... I retract that .... DON'T FUCKING MOVE FROM THAT SPOT Not even a Planck Action, it will make it that much more hell for these particles, you think you have to work hard these little guys have to work zillions of times harder even if you had to build this moving Big stones all day.

There are some serious infinities I had to dodge to get it like that which was why Du2φ2 was chosen to join it at via φ2 = φ2 try to join it at Dirac or Yukawa and see what happens.

I get it man, which is why it is probably like that. I always noticed they are/were/will be a very odd particle which is why Es ≈ h(ωs/2π) Es being energy of graviton don't dig deeper than that or you will regret it.

If this is true no wonder Gravitons are so screwed up having meditate gravity across all this shit which I have an idea what it is but ya.

I dunno but it is better now after it canceled. Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,S) = ((ħωs)((|(Log(DgDaDψDφ-W)(( (Mp2/2)R - (1/4)FaμvFaμv + i(ψ-bar)γμDμψi +(ψ-bar)iLVijφψjr + (h.c.) - V(φ)/-Dμ2)|)-e2S(r,t)/h)) - (Mbωs(ksGuv./guv8πG)1/2 + mk2)Rs2/2)((|(Log(DgDaDψDφ-W)(( (Mp2/2)R -(1/4)FaμvFaμv + i(ψ-bar)γμDμψi +(ψ-bar)iLVijφψjr + (h.c.) - V(φ)/-Dμ2)|)-e2S(r,t)/h))) / (ħ2/2Mb)((|(Log(DgDaDψDφ-W)(( (Mp2/2)R - (1/4)FaμvFaμv + i(ψ-bar)γμDμψi +(ψ-bar)iLVijφψjr + (h.c.) - V(φ)/-Dμ2)|)-e2S(r,t)/h)))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)(2ħωs)) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0) What does h.c. mean? Figured it out. aji Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,S) = ((ħωs)((|(Log(DgDaDψDφ-W)(( (Mp2/2)Rs - (1/4)FaμvFaμv + i(ψ-bar)γμDμψi +(ψ-bar)iLVijφψjr + (aji.) - V(φ)/-Dμ2)|)-e2S(r,t)/h)) - (Mbωs(ksGuv./guv8πG)1/2 + mk2)Rs2/2)((|(Log(DgDaDψDφ-W)(( (Mp2/2)Rs -(1/4)FaμvFaμv + i(ψ-bar)γμDμψi +(ψ-bar)iLVijφψjr + (aji) - V(φ)/-Dμ2)|)-e2S(r,t)/h))) / (ħ2/2Mb)((|(Log(DgDaDψDφ-W)(( (Mp2/2)Rs - (1/4)FaμvFaμv + i(ψ-bar)γμDμψi +(ψ-bar)iLVijφψjr + (aji) - V(φ)/-Dμ2)|)-e2S(r,t)/h)))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)(2ħωs)) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0) Mordred you have turned my equation into literal gravity hell now which is probably right but still.

Log(DgDaDψDφ-W)((id4xg1/2 (Mp2/2)R - id4xg1/2(1/4)FaμvFaμv + id4xg1/2i(ψ-bar)γμDμψi + id4xg1/2((ψ-bar)iLVijφψjr + (h.c.)) - V(φ)/-id4xg1/2Dμ2) = φ2 Transform. Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,S) = ((ħωs)((|(Log(DgDaDψDφ-W)((id4xg1/2 (Mp2/2)R - id4xg1/2(1/4)FaμvFaμv + id4xg1/2i(ψ-bar)γμDμψi + id4xg1/2((ψ-bar)iLVijφψjr + (h.c.)) - id4xg1/2V(φ)/id4xg1/2Dμ2)|)-e2S(r,t)/h)) - (Mbωs(ksGuv./guv8πG)1/2 + mk2)Rs2/2)((|(Log(DgDaDψDφ-W)((id4xg1/2 (Mp2/2)R - id4xg1/2(1/4)FaμvFaμv + id4xg1/2i(ψ-bar)γμDμψi + id4xg1/2((ψ-bar)iLVijφψjr + (h.c.)) - id4xg1/2V(φ)/-id4xg1/2Dμ2)|)-e2S(r,t)/h))) / (ħ2/2Mb)((|(Log(DgDaDψDφ-W)((id4xg1/2 (Mp2/2)R - id4xg1/2(1/4)FaμvFaμv + id4xg1/2i(ψ-bar)γμDμψi + id4xg1/2((ψ-bar)iLVijφψjr + (h.c.)) - id4xg1/2V(φ)/-id4xg1/2Dμ2)|)-e2S(r,t)/h)))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)(2ħωs)) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0) Like I said what can Absolutely never be calculated that. where it wouldn't even let put the symbol for ψ bar Where id4xg1/2 cancels. Log(DgDaDψDφ-W)((id4xg1/2 (Mp2/2)R - id4xg1/2(1/4)FaμvFaμv + id4xg1/2i(ψ-bar)γμDμψi + id4xg1/2((ψ-bar)iLVijφψjr + (h.c.)) - id4xg1/2V(φ)/-id4xg1/2Dμ2) = φ2 Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,S) = ((ħωs)((|(Log(DgDaDψDφ-W)(( (Mp2/2)R - (1/4)FaμvFaμv + i(ψ-bar)γμDμψi +((ψ-bar)iLVijφψjr + (h.c.)) - V(φ)/-Dμ2)|)-e2S(r,t)/h)) - (Mbωs(ksGuv./guv8πG)1/2 + mk2)Rs2/2)((|(Log(DgDaDψDφ-W)(( (Mp2/2)R -(1/4)FaμvFaμv + i(ψ-bar)γμDμψi +((ψ-bar)iLVijφψjr + (h.c.)) - V(φ)/-Dμ2)|)-e2S(r,t)/h))) / (ħ2/2Mb)((|(Log(DgDaDψDφ-W)(( (Mp2/2)R - (1/4)FaμvFaμv + i(ψ-bar)γμDμψi +((ψ-bar)iLVijφψjr + (h.c.)) - V(φ)/-Dμ2)|)-e2S(r,t)/h)))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)(2ħωs)) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0)

Yes that has to be pulled through the higgs based on that image, Du2φ2 where φ2 = φ2 , So there will be a logarithm of some sort

solve thourgh Yukawa Coupling where φ2 or Dirac not sure of which or both?

Es = h(ωs/2π), Never took the simple solution huh isn't much easier like that, not being like this, which are both the graviton, S = 2 Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,S) = ((ħωs)((|φ2|)-e2S(r,t)/h)) - (Mbωs(ksGuv./guv8πG)1/2 + mk2)Rs2/2)((|φ2|)-e2S(r,t)/h))) / (ħ2/2Mb)((|φ2|)-e2S(r,t)/h)))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)(2ħωs)) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0) back to ≈ Eb(t,ω,R,M,I) = ∇(1/((1-(((2MbG / Rs) - (Isωs2/2Mb) + V)2/C2))1/2))MbC2

Transform again So, (Mbωs((ksGuv./guv8πG)1/2 + mk2))Rs2/2) = V(r,t) = Mω2r2/2 Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,S) = (Ê((|φ2|)-e2S(r,t)/h)) - (Mbωs(ksGuv./guv8πG)1/2 + mk2)Rs2/2)((|φ2|)-e2S(r,t)/h))) / (ħ2/2Mb)((|φ2|)-e2S(r,t)/h)))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0) Which badly needs to be simplified, In any case, where Transform Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,S) = ((ħωs)((|φ2|)-e2S(r,t)/h)) - (Mbωs(ksGuv./guv8πG)1/2 + mk2)Rs2/2)((|φ2|)-e2S(r,t)/h))) / (ħ2/2Mb)((|φ2|)-e2S(r,t)/h)))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0) which looks right, which d3p = 2E = 2ħωs being a negative probability in the Klein Gordan equations. Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,S) = ((ħωs)((|φ2|)-e2S(r,t)/h)) - (Mbωs(ksGuv./guv8πG)1/2 + mk2)Rs2/2)((|φ2|)-e2S(r,t)/h))) / (ħ2/2Mb)((|φ2|)-e2S(r,t)/h)))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)(2ħωs)) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0)

Energy Eighenvalue transform. Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,Ψ) = (ÊΨ(r,t) - V(r,t)Ψ(r,t) / (ħ2/2Mb)Ψ(r,t))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0) Ψ Transform. Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,S) = (Ê((|φ2|)eiS(r,t)/ħ)) - V(r,t)((|φ2|)eiS(r,t)/ħ))) / (ħ2/2Mb)((|φ2|)eiS(r,t)/ħ)))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0) S Quantum number transform. Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,s) = (Ê((|φ2|)ei(s(s+1))1/2)) - V(r,t)((|φ2|)eis(s+1)1/2))) / (ħ2/2Mb)((|φ2|)eis(s+1))))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0) Where I cannot do that already a exponent. Split ħ into h/2π Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,S) = (Ê((|φ2|)ei2πS(r,t)/h)) - V(r,t)((|φ2|)ei2πS(r,t)/h))) / (ħ2/2Mb)((|φ2|)ei2πS(r,t)/h)))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0) Transform Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,S) = (Ê((|φ2|)-e2S(r,t)/h)) - V(r,t)((|φ2|)-e2S(r,t)/h))) / (ħ2/2Mb)((|φ2|)-e2S(r,t)/h)))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0)

Where I still forgot G in ab to uv Split and detransform back to ωs to make it the same as Cosmo ∇Eb(x,y,z,t,M,I,k,φ,ρ,m) = ∇(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/C2))1/2))MbC2 Which Cut E= MC2 and (1/f((x,y,z,t,M,I,k,φ,ρ,m))) ∇'(x,y,z,t,M,I,k,φ,ρ,m) = ∇((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/C2))1/2) Reverse Solve ∇(x,y,z) = ∇'(x,y,z,t,M,I,k,φ,ρ,m)((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/C2))1/2) Absorb Schrodinger Equation. iħ(d/dt)Ψ(r,t) - V(r,t)Ψ(r,t) / (ħ2/2M)Ψ(r,t) = ∇2 ∇'(x,y,z,t,ω,M,I,k,φ,ρ,m,Ψ) = (iħ(d/dt)Ψ(r,t) - V(r,t)Ψ(r,t) / (ħ2/2Mb)Ψ(r,t))1/2((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/C2))1/2) Reaquire E= MC2 and (1/f((x,y,z,t,M,I,k,φ,ρ,m))) Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,Ψ) = (iħ(d/dt)Ψ(r,t) - V(r,t)Ψ(r,t) / (ħ2/2Mb)Ψ(r,t))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/C2))1/2))MbC2 Where Then C2 = (1/ε0 μ0) Eb(x,y,z,t,ω,M,I,k,φ,ρ,m,Ψ) = (iħ(d/dt)Ψ(r,t) - V(r,t)Ψ(r,t) / (ħ2/2Mb)Ψ(r,t))1/2(1/((1-(((2MbG / Rs) - (Isωs(ksGuv./guv8πG)1/2 + mk2)/2Mb)+ (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ks(1/ε0 μ0)/Rs2) + (ksGuv/guv8πG ))1/2(ΔKiloparsec)))2/(1/ε0 μ0)))1/2))Mb(1/ε0 μ0)

Ya, there is a problem with using that for the Cosmo k and p do not equal zero that would be devoid of matter, but it does = k ∇Eb(x,y,z,t,ω,M,I, φ,ρ,m) = ∇(1/((1-(((2MbG / Rs) - (Isωs(ks2 + mk2)(1/2)/2Mb) + (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (ks2))1/2(ΔKiloparsec)))2/C2))1/2))MbC2 Where now I am going to fully transform ωs to ks2 + mk2 because of that. ∇Eb(x,y,z,t,M,I,k,φ,ρ,m) = ∇(1/((1-(((2MbG / Rs) - (Is(ks2 + mk2)/2Mb) + (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (ks2))1/2(ΔKiloparsec)))2/C2))1/2))MbC2 Where it does literally say that it is caused by Spin/Curvature DE. and Gaussian Curvature = 1/r2 in a sphere, which is k1k2 = K = k2 Where K = Rab/gab Where Rab = kTab Where this is about to go through a transform. ∇Eb(x,y,z,t,M,I,k,φ,ρ,m) = ∇(1/((1-(((2MbG / Rs) - (Is(ksTab./gab) + mk2)/2Mb) + (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (ksTab/gab ))1/2(ΔKiloparsec)))2/C2))1/2))MbC2 Where Now Another Transform. ∇Eb(x,y,z,t,M,I,k,φ,ρ,m) = ∇(1/((1-(((2MbG / Rs) - (Is(ksGab./gab8π) + mk2)/2Mb) + (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (ksGab/gab8π ))1/2(ΔKiloparsec)))2/C2))1/2))MbC2 (a,b) >(u,v) transform and ∇Eb(x,y,z,t,M,I,k,φ,ρ,m) = ∇(1/((1-(((2MbG / Rs) - (Is(ksGuv./guv8π) + mk2)/2Mb) + (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (ksGuv/guv8π ))1/2(ΔKiloparsec)))2/C2))1/2))MbC2

So, I am missing a coordinate ∇Eb(x,y,z,t,ω,M,I, φ,ρ,m) = ∇(1/((1-(((2MbG / Rs) - (Isωs(ks2 + mk2)(1/2)/2Mb) + (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (Λ/3))1/2(ΔKiloparsec)))2/C2))1/2))MbC2 Then Λ =

Yes, where the Langrangians agree with the coordinates used upon density in four current like I had thought you were gonna do which is why I took the equation then stuck matter density for that rather than moment of inertia being for that in L form when the Hubble's Constant was inserted. ∇Eb(x,y,z,t,ω,M,I,ρ,m) = ∇(1/((1-(((2MbG / Rs) - (Isωs(ks2 + mk2)(1/2)/2Mb) + (((8πG/3)((g/(2π)3)∫(p2 + mp2)(1/2)(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (Λ/3))1/2(ΔKiloparsec)))2/C2))1/2))MbC2 Where ρ(x,y,z,t) = r(x,y,z,t), I assume the function itself is φ being d3p

and why doesn't = R

Okay, I got that but I really don't want to construct one but once.

i(That) + j(That) + k(That) - Ct(That) past that you gotta know the signs but ..... (-/+).....n

You have to reverse how I constructed to see the different parts, the first seven are SR/GR, First four are four current SR

Yes, which is why ∇Eb(x,y,z,t,ω,M,I,ρ,m) = ∇(1/((1-(((2MbG / Rs) - (Is(ks2 + mk2)/2Mb) + (((8πG/3)((g/(2π)3)∫(p2 + mp2)1/2(1/e((E - μ)/T)±1)d3p) - (ksC2/Rs2) + (Λ/3))1/2(Δx/3.08567758128*1019)))2/C2))1/2))MbC2 says ∑∑∑∑∑∑∑∑∑∇

thats why I keep adding them as I defined or someone else does.

Something like that which in Quantum Machinery is called a String Computer.

Yes, but humans are not that smart in math, this is something a Hypercore would have to do and I am not saying Binary Hyper-threading either like I said what can stack a quantum computer this equation.