Dalo

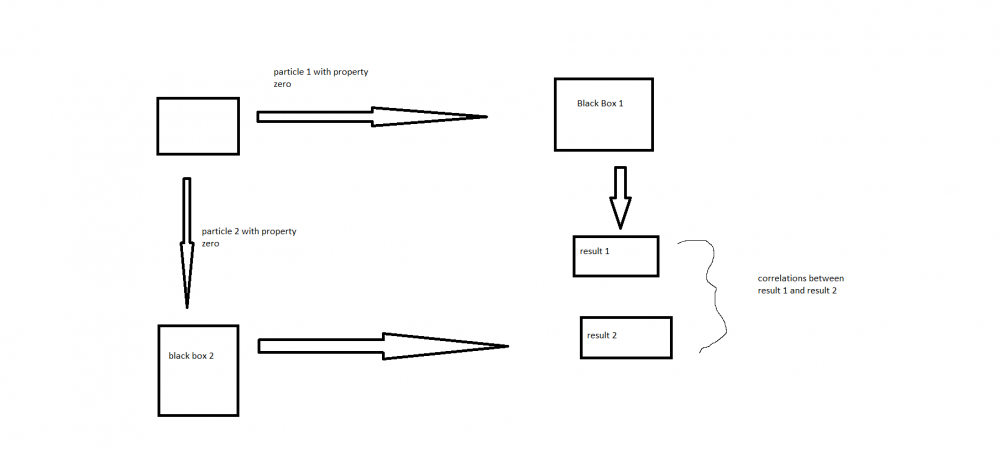
"If the reader is puzzled by the particulate nature of light it may help to note that experiments similar to the ones we will describe can also be carried out on protons and electrons, archetypical particles. In those cases one measures the so-called “spin” of the particles by passing them through an inhomogeneous magnetic field." (p.11-12) "If the filters are misaligned, then the photons still behave as if they have the same polarization."(p.12) All these properties are irrelevant in our case, because what is at stake in the example given are the statistical correlations between photon 1 and photon 2 concerning (non circular) polarization. In another case it could be spin, or some other properties like you mentioned. The logic would, I think, still be the same. Except that, as I have made perfectly clear, I have limited my claim to examples like that given by Maudlin. Baby steps. Remember? *** Any difference between photon 1 and photon 2, like circular polarization, would break entanglement. and make the whole argumentation void. That would be the end of this part of quantum theory.

If your example applies to the same problem then Maudlin is wrong and I shouldn't have taken him at his word. The quote is not mine, but a literal quote from p.12 of the book. I will see if I can find one similar to this one in the article you have shared.

Congratulations. You have put the finger on the weak spot of my argumentation. Those were my two fundamental assumptions: 1) When both photons leave the atom, they have the same polarization; 2) both filters can be considered as identical. There are some problems though with this objection. It would be a hidden variable theory and therefore would negate the possibility of entanglement. The entanglement conclusion only works with both assumptions. That is also the opinion of Maudlin. I have already posted one or more quotes where he emphatically presents the photons as having the same polarization at the outstart. My assumptions therefore are not something I have dreamed up, they are an essential part of any entanglement experiment. Once you accept that, the problem becomes very simple: Both photons and both filters are interchangeable. It would be like if we had one single photon and two filters. It would therefore not be surprising that the same correlations would manifest themselves in both cases. I can do that because they are irrelevant to my case. Polarization is the example Maudlin have taken, and I followed him in that. It could have been the spin of an electron, the logic would not have changed. It comes down to this

Because it does not matter! It is a matter of logic, it has nothing to do with the actual correlations. The only important thing is that these correlations have to be the same as determined by quantic statistical regularities. You insist on turning it into a technical matter that can be solved by technical means. I say it is a matter of logic. Once you have accepted that both situations are different, then you must accept entanglement and non-local variables as Bell did. But my whole point is that both situations are in fact equivalent. And you can only prove that by logic and the empirical facts from which the whole situation starts: 1) both photons have the same polarization, 2) both filters are identical in the sense that they could be swapped without changing the experiment. I am sorry, but I cannot make it clearer than this. And if you still think after my explanation that it still is a mathematical or a physics problem then all I can do is give up, because we will keep talking alongside each other, and that would be a waste of time for all of us.

Finally! This The most important question of all that has been asked in this thread. Maybe explaining it as simply as I can will reveal any mistake in my reasoning and we can all go sleep tight and have nice dreams. 1) The photons, when they leave the atom and go each right or left, are already polarized! 2) In other words, when they go through the first filter, it is in fact equivalent to a non-polarized beam going through a second filter, after having been through the first. 3) If both the filters through which photon 1 and photon 2 have to go are oriented the same way, both photons will either pass or both will be absorbed. 4) let us now misalign both filters by an angle alpha. Photon 1 will be transmitted/absorbed by filter 1 in a certain ratio. 5) Photon 2 has now to go through filter 2 that is misaligned by an angle alpha relatively to fiilter 1. 6) But photon 2 has the same polarization as photon 1 before the latter went through filter 1. 7) That means that we could easily swap photon 1 and photon 2 before any passes their respective filter. 8) When photon 2 goes through filter 2, it reacts exactly as photon 1 would do if it also had to go through the same filter (2). 9) But since photon 1 has gone through filter 1, when you compare both you get the same correlations as if you had first put photon 1 through filter 1... 10) Then, magically, had undone all changes on photon 1, and passed him through filter 2. 11) comparing the result of photon 1 and filter 1 with the result of the same photon 1 with filter 2, and then the result with photon 2 through filter 2, you would find them identical. I know, I feel a little bit dizzy too! If you find my list too confusing remember the golden rule: both photons have the same polarization, and they will react therefore the same way to the same direction of a filter, or to a misalignment alpha.

I have edited my previous post. I think that I answered your question there.

in this case, no. edit: what I am claiming is that both photons, in the polarization example can be considered as local. Each photon is reacting exactly as the other one would if it would have had to go successively though two polarizers having the same direction as the other two. In this sense, they are both local, and do not influence each other in any way. They react the same because they are identical and the filters they go through are also identical. A very simple explanation. Maybe too simple. But nobody has proven it wrong yet.

I do not need a lesson on non-locality. I had a very specific question, which was in fact off-topic, concerning polarization. Instead of trying to explain to me what non-locality is, maybe you could try and show me how my interpretation of it is faulty, and why therefore my claim is wrong. My whole claim says that the concept of non-locality is wrong and that entanglement is the result of a theoretical bias. This is the point that you should tackle. I also said that I would not be surprised if somebody proved me wrong because I am aware of how pretentious my claim sound. Unluckily I have not read a single argument that took my claim and my arguments seriously. It was all about polarization, philosophy, ignorance of physics laws, or, last, in your reaction, a reference to what non-locality and entanglement mean. I know what they mean. I am trying to show that what they say cannot be true. Maybe I am wrong, and so, I am just waiting for somebody to show me why and how I am wrong. Can you do that? I also said, it is not a matter of mathematics or physics, but a matter of interpretation. If it were a pure mathematical or physical problem I would have stayed away from it. I understand this is a Physics forum and people are not used to approach some issues philosophically instead of mathematically or "physically", but I cannot help it that some problems do belong (also) to philosophy. Yes, but then there are so many versions of it that you will have to be more specific.

It is obvious you are not addressing the issue. The point is non-locality. Polarization is here an illustration of the problem. A mere example. It is often presented not with polarization but, for instance the spin of a particle. Limiting the discussion to polarization is meaningless. https://en.wikipedia.org/wiki/Quantum_nonlocality Yes, and that was also von Neumann's main argument. Only Bell limited the validity of this argument to local hidden variables. There was no way probabilities could add up to the same statistical regularities everybody considers as valid (including me). The difference between von Neumann's and Bell's analysis is that Bell left the possibility open for non-local hidden variables. https://en.wikipedia.org/wiki/Hidden_variable_theory That does not change my claim which takes into account both these theories. See my first 5 or 6 posts.

The Sorbonne, Paris, France. You?

saying it is not enough. You have to show it. The idea that one cannot discuss QT without involving RT is really strange.

As a philosopher I can assure you that it is the most absurd affirmation you could ever express. Feel free to ask specialists in the philosophy of Physics. It is also an avoidance strategy that does not do honor to the members of this forum.

Thank you. Your link does not help much, it is too mathematical for me. I withdraw my question concerning the 50-50 rule. I suggest we get back to the main subject of this thread and I apologize for the waste of time.

Good. Let us get back to what is the main point of this thread. You were right to say that it is not about polarization. But when I said that I simply meant that the example used by Maudlin and that I was analyzing concerned polarization. I repeat my previous remark to Klaynos: I have no trouble understand this. What I still do not understand is why it holds only for the first filter, and not for the second one.

As my previous remarks show, it is the difference between how the first polarizer reacts compared to the second. edit: Maybe I should, as suggested, start a thread dealing exclusively with polarization. But may I remind you all that I have used the results as given By Maudlin. And, yes, I understand them! I did not use my own ideas about polarization for the simple reason that I do not have any. So, even if you think I am ignorant of some necessary laws, all you have to do is show that I misunderstood Maudlin. Also, remember that I was the one who admitted that I did not understand the 50-50 of the first filter, and I still don't. That didn't stop me from analyzing Maudlin's arguments and expressing my claim. Which nobody has proven wrong. Everybody is happy to hammer on my ignorance. An ignorance I admitted. So, why no go back to the subject of the thread, or is it too "metaphysical" for this forum?

". Malus's law /məˈluːs/, which is named after Étienne-Louis Malus, says that when a perfect polarizer is placed in a polarized beam of light, the irradiance, I, of the light that passes through is given by I=I_{0}\cos ^{2}\theta _{i},} where I0 is the initial intensity and θi is the angle between the light's initial polarization direction and the axis of the polarizer. A beam of unpolarized light can be thought of as containing a uniform mixture of linear polarizations at all possible angles. Since the average value of \cos ^{2}\theta } is 1/2, the transmission coefficient becomes From https://en.wikipedia.org/wiki/Polarizer#Malus's_law_and_other_properties Here is what I do not understand. This law explains perfectly why, mathematically speaking, 50% of the light is transmitted or absorbed. But the laws speaks of an average direction, so only directions close to (there is no perfect polarizer), should be transmitted or absorbed. Let us say that 5 is the average of 1-10. According to Malus, in one case 1,2,3,4,5 are transmitted, and 6,7,8,9,10 are absorbed, and vice versa. [or 4,5,6,7,8, or some such combination) That is a very generous interpretation of "average", especially if we consider that the second filter is much more critical. There, no "average" is allowed, either you belong to one direction or you are refused entrance. Did I also understand it wrong? In that case, please bear with me and explain it to me. Concerning your other remarks, I will abstain from any comment.

I may have wandered in out of my depth, but I kept repeating that I would certainly not be surprised if somebody proved me wrong. I have faithfully presented Maudlin's example and arguments and I know enough about polarization to know that not a single author has ever explained why the first filter absorbs or transmits 50% of the beam, while the second filter does that according to the angle of misalignment. Maybe you know the answer that I could not find anywhere, and that neither Swansont nor Mordred have given until now. If you do not either, then climb off your high horse please. If you do know and are willing to share it I will be eternally grateful and will apologize deeply and profusely.

Apparently nobody knows why the first polarizing filter absorbs or transmit 50% of the beam. It makes you wonder how quantum scientists dare draw any conclusion regarding the behavior of a second photon (identical to the first) and a second filter (identical to the first). I mean, they are not even able to give a complete account of the initial conditions! By the way, I don't mean a "metaphysical why", but a plain common "physical why" that would explain why light (be it a wave and/or a particle) reacts this way to a first polarizer, just to change completely its front door policy right after. But maybe I am too impatient, and I should just wait for somebody to explain to me the nuts and bolts of this physical phenomenon.

THERE'S NO FIRE HERE! NO FIRE! http://residentevil.wikia.com/wiki/Anna_Bolt?file=Anna_yells_at_the_Red_Queen.jpg

Again you are right. But non-local in the context of the debate Bohr-Einstein, and also in the context of Maudlin's article which you have shared, is unambiguous. There could be no misunderstanding about which sense of non-local was used. And neither you nor Swansont misunderstood the meaning. There are many words, not all of them technical terms, that have multiple meanings (polysemy) and which only get a precise meaning not by explicit declarations but by the context of their use. I am not responsible for the associations created by those words. The context should always come first. I do not think there could be any ambiguity concerning the context of my thread. edit: nowhere in the literature about (non)-locality in QT did I encounter the other meanings of this expression. Not a single author I know of felt the need to expand on the different meanings of (non-)locality, and how different it is from (non-)locality in RT or cosmology.

I am afraid I don't.

That sounds like a good advice, but didn't I do that implicitly in the description of the problem I was studying and the claim I was presenting?

You won't mind then if I do not go into all those different kinds of non-locality, of which by the way I have no understanding.