Dalo

That is exactly the point which I do not understand. Light, once polarized, can have any direction. before it is polarized it has all possible directions, so why would a polarizer absorb or transmit 50% and not a percentage equivalent to the direction of the polarizer? ************************************ I do not doubt the validity of what you are saying, only its relevance to the subject of the thread. Non-locality in QT is not what you are describing. **************************************** I would honestly not be surprised at all if somebody knocked off my argumentation. After all we are talking about the greatest minds in Physics, and there would be no shame for me if it turns out that I have overlooked some essential elements, and been misled to the wrong conclusion. But I do not understand your objection, because that is exactly what Maudlin pretends. He states explicitly that both photons show the same polarization. I do not know of other properties, but they do not seem to be relevant to the experiment. It is all about the direction of polarization. That is also a fundamental point of the issue: the statistical regularities. I have never assumed a deterministic correlation: 100% passed or absorbed, or any other invariable percentage..

Well, I must say that your definition of non-local is very clear. I just wonder whether it can be applied to the discussion at hand. Because, if you are right the whole debate between Bohr and Einstein, and its follow up even up to the 21st century is a waste of time. Einstein and his friends (EPR, Schrödinger) had apparently no idea of the meaning of non-locality. Congratulations, your solution is even simpler than mine: non-locality is a non-problem.

That is of course always possible. But we won't know until you have dazzled us with your knowledge of what non-locality really means.

I said I have no idea what the drawing is supposed to mean. You should make it clear, you brought it in. Perhaps you should confirm in a few words exactly what you think non locality means. ************************************************** "Definition the returns of the disposition of any ray to be reflected I will call its fits of easy reflection, and those of its disposition to be transmitted its fits of easy transmission..." [see also Proposition XVII ff] Isaac Newton (Second Book of) Opticks. Just like with polarization, we can determine empirically the percentage of light reflected or transmitted through glass of variable thickness, but like Feynman confirmed, we have no explanation for the phenomena. We can then search for the explanation of this very local phenomena in a mysterious entanglement or in non-local hidden variables. I am convinced that we would be then looking in the wrong place. The mystery lies in the interaction of light with glass or polarizing filters. I have asked about the fact that the first polarizer absorbs or reflects 50% of the beam because it seems mysterious to me when compared to the percentages created by the second filter. We have no idea why the percentages are what they are. In fact, Feynman uses our ignorance not to encourage us to look for a solution, but to convince us of abandoning the search: Nature is just what it is, probabilistic, and there is no reason to search for something else besides probabilistic regularities.. This is turning your ignorance in a metaphysical property of reality, thereby justifying this ignorance.

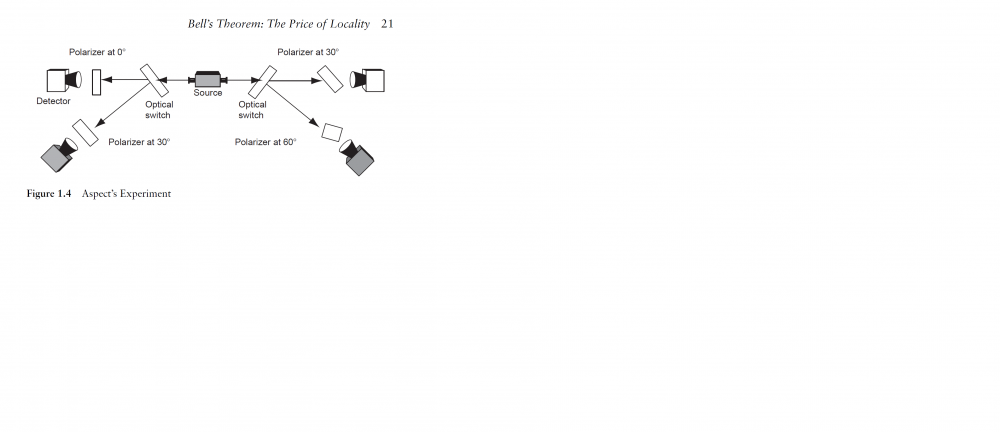
I would like to point out that my analysis also holds in the case of the famous Aspect experiment of 1982. After all, two fundamental conditions are fulfilled. 1) Both photons are identical, 2) both photons undergo measurements by identical devices.

I am not sure what it is supposed to mean. I know the drawing, forgot its name, looks likes Escher's drawings. I have read some Penrose, but certainly not enough to pretend to know his ideas. What I remember of him is his attempt to link consciousness with quantum theory. Not very convincing.

http://www.scienceforums.net/topic/112284-non-locality/?do=findComment&comment=1029121 In that post I have posited my main claim that the so-called entanglement of both photons is in fact the mere result of a metaphysical, or at least theoretical bias. That is at the same time an explanation as to why my solution has never been presented (as far as I know!) before. It seems so simple, would you say. There must be a reason why nobody has considered it. I must admit that I am facing the same wonderment, and I have read and re-read the arguments presented by Maudlin, convinced that I had overlooked some simple fact that would make me look like a fool. There is nothing difficult in what I say: both photons show the same behavior and the same statistical regularities for the simple reason that they are identical to each other, and so are the polarizing filters. The distinction between local and non-local is therefore meaningless! But if it were that simple, why hasn't anyone come up with the idea then? I think that the reasons must be sought not in the logical thinking of all the participants, their intelligence and expertise are certainly beyond doubt. It would be certainly pretentious, and plain ridiculous, from my part to claim any kind of intellectual superiority. So. once again, why is that, and isn't that a clear sign that my view must be simply wrong, or at least seriously flawed? The possibility cannot of course be eliminated, but I will nevertheless try and defend my point of view. The first indication is given in the "translation" that Maudlin gives of the issue. He imagine people trying to develop a guessing strategy that would lead to the same regularities as the quantum experiments. That is, I think, (and here I must rely on my "biased", verbal knowledge of von Neumann's and of Bell's argumentation), what everybody has tried to do for almost 100 years. That is, I am convinced, the wrong approach. It implies that the statistical regularities, which I consider, just like everybody else, as unattackable, are the last word in Physics. This in turn means that even Bell, at least subconsciously, and following Einstein, takes those regularities as what has to be directly explained. Not that he should doubt their validity, but, just like Einstein, Bell should have at least asked himself whether hidden variables were needed to explain those regularities. If they had done that, then they would have stood still by the way these regularities were obtained. In fact, they were so convinced that the results obtained were objectively valid and beyond discussion, that they never considered that these results were themselves the result of the way their knowledge was obtained. Maybe Einstein, and perhaps also Bell, was afraid of conceding a fundamental point to Bohr: the statistical regularities were themselves created by the experiment! If Einstein had admitted that, at least to himself, he would probably immediately have come to the same conclusion I reached: The second photon and the second filter create together a system that is indistinguishable from the first photon and filter. It is therefore not surprising that Bohr, who was maybe already convinced that nature was probabilistic, thought that the photons were entangled. It is certainly ironic that Bohr did not recognize one of his main epistemological principles: the regularities were the result of the experimental setup. But then, that same epistemological principle would have indicated that the so-called "hidden variable" was in fact hidden in plain view, and that therefore a deterministic explanation could certainly not be excluded.

This is the part I used of Scarani's book. scarani 23-30.pdf

You can find in the text attached the few pages concerning the example I will be analyzing. It can be opened by windows viewer, but should easily be converted to another format. polar 19-25.xps polar 19-25.pdf mine left me a long time ago ******************************* In Maudlin's book, the part about polarization, he mentions the fact that any filter, whatever its direction, absorbs half of the photons and let the other half pass. I have come across this rule many times, but I could never make sense of it. Could you explain it in easy words, or have you maybe a link I could look up? Thank you.

well said.

If there is one thing that the history of philosophy can teach us is that Reality is a metaphysical concept. That may sound strange to members of a Physics forum, so allow me to elaborate. Already more than 2000 years ago Plato was convinced that the real world we live in is but a shadow of "the Real World". We are like prisoners in a cavern, unable to leave it and look outside. All we can can see are moving shapes projected on one of the walls, representing the "pure forms" that constitute the eternal objects of which our everyday objects are mere fleeting copies. Kant, in the 18th century, had a somewhat similar conception, even if he was a fervent admirer of "modern" science. For him, Reality is for ever unknowable. He called it the noumen, in opposition to the phenomen which belongs to our everyday world, and which is studied by science and philosophy. What both authors had in common, is the deep conviction that reality is rational and can be expressed in causal relationships between objects and processes. This, whatever the nature of the metaphysical Reality. Bohr abandoned this conviction, or at least reformulated in a way that better suited his theoretical needs. [I am sorry I cannot provide a reference in which I read that Bohr had been deeply influence by his philosophy teacher. I just can't seem to remember where I read it]. Instead of being driven by causal rules, Reality became itself probabilistic. This a very important fact, since it implied that Bohr's Reality had also lost an essential property: it was no longer unknowable! That would have been the case if probability had remained a property of our knowledge instead of a fundamental property or Reality itself. Einstein could not abide by this conviction, and even though, as Maudlin and many other authors, emphasize that he has never considered determinism as a precondition of doing physics (p.9 ff of Maudlin's article), his "God does not play dice" is clearly meant to distinguish his views from Bohr's concerning reality and (local) causality. What Einstein did not realize is that he, just like Bohr, lets science define reality. Maybe God (as the perfect epistemological subject ) does not play dice, but the only one who knows that is God Himself! God is therefore also the only one who can say whether Bohr or Einstein, or both, or none of them, is/are right or wrong. Science can only define its own reality, and it does that not through mathematical or empirical arguments, but through philosophical, metaphysical, or even religious convictions. That is why the concept of "entanglement" is not so much a physical principle, as a metaphysical one. It only makes sense in a metaphysical model where reality itself is probabilistic.

Yes. That is why I won't be doing anything else until I have studied it. I think there have been enough misunderstandings between us in the near past.

Thank you. I did not have this article. I was using his book "Quantum Non-Locality & Relativity", edition of 2001. But I cannot imagine that he would say different things in the one or the other. The article is much shorter, and that will certain come handy to look up things quickly.

You have explained the principles of entanglement succinctly and clearly. I will try in my following posts to show how some points are confirmed (no spooky action at a distance, statistical regularities), while others are reformulated (superposition, local and non-local). I hope to show that the way we approach nature and reality in general, and quantum events in particular, determines our interpretation and the mathematical tools we use. I will not go into the value of the tools themselves, nor into the way they are applied to the issue.

I have no problem with that. I cannot judge of the value of any mathematical tool and will be happy to rely on your expertise. ****************************************** @Mordred I would really appreciate it if you could give a step by step explanation of von Neumann's argumentation about the impossibility of hidden variables, and Bell's Theorem. As I said, I have to rely on verbal, non-mathematical presentations, but I am always afraid of missing the subtleties inherent to a mathematical argumentation. It would therefore be a great help, and not only for me, if you walk me through it. I do not know if it is feasible and how much time it would take, But I am sure it would be a valuable contribution to this forum in general.

First, I thank you for your efforts and for the links. I would like to finish my argumentation first, so that you will have the whole to look at and critically dissemble. Otherwise we may risk to talk alongside each other again, instead of listening to each other. I think I may say that, instead of dealing first with the information you have given, and this for the following reasons: I do not question the statistical regularities in quantum theory. I have deliberately given imaginary percentages of photons transmitted and absorbed depending on the angle of misalignment, to emphasize the fact that they are irrelevant to my position. Even if they are fundamental to quantum experiments and theory. My arguments are not mathematical, and neither statistical nor physical. I do not attempt to explain the statistical regularities, nor do I have any inkling as to how they could be explained mathematically or statistically. I completely lack the expertise to do so and therefore stay far away from such arguments. In fact, as far as I can do that as a layman and philosopher, I agree with the general idea that no hidden variable theory can be mathematically proven. Because of their mathematical nature, I would not dare distinguish between von Neumann's argumentation and Bell's. I can only go on the verbal explanations of both authors, void of any equations, and that of other writers. This is where I base, let us call it by its rightful name, my "biases" upon. Since I cannot rely on my comprehension of the mathematical proofs, I only have my logic and intuition to work with. Those mental faculties are under great attack by the majority of the quantum theorists, we are supposed not to trust them. I think that is presumptuous. You can claim anything you want and then tell your audience that it is their fault if they do not understand. They just have to let go of their logic and intuition. That I cannot accept. Which brings me in frontal (philosophical) collision with certain interpretations (not facts or experiments) of quantum theory. The debate between von Neumann and Bell proves at least one thing to me as a philosopher. Any mathematical solution to the hidden variable theories, and therefore to quantum entanglement, is controversial, to say the least. That is why I certainly have no desire to defend/attack one or the the other. I hope to show in my following posts, that it is a matter of fundamental interpretation, of philosophy, and not of mathematics. This brings me to the EPR paper which I have read very carefully about a year ago, and which I intend to re-read as carefully. I can tell you what I thought at that time,;maybe I will look at it differently, having read other authors since then, but it is unlikely. I am not a fan of Einsteins view of science and reality. I think that it is rather simplistic and explains, at least for a part, why Bohr could so easily defuse Einstein's arguments. But I take Heisenberg's Principle very seriously as a philosopher, and because I think that it is in principle applicable to both the microscopic and macroscopic domains, with of course very different practical consequences, it should not be used as an automatic endorsement of the Copenhagen interpretation of QT. These are a few points that come to mind to explain why, without in any way denying their utility and value, I will probably not make use of the information you have so generously given over Statistics and QT. I would like to avoid a sterile debate where I am supposed to accept a mathematical approach while I am arguing that it is not a mathematical problem. This has nothing to do with mathematics in general. As I said before, they are an indispensable tool and modern science would be unthinkable without them. But mathematics are always guided by "deeper" principles, being the own philosophical and metaphysical convictions of mathematicians and physicists. To avoid any misunderstanding, I am not talking about the calculations which form the heart of any mathematical argument, but about the premises and the goals which are, almost, never completely free from non-mathematical considerations. In short, I hope to show in this thread that entanglement as a concept, is not a pure mathematical concept, but is born from non-mathematical considerations, to put it rather vaguely. I can therefore only react to criticism that takes into account my starting point. If it were a mathematical issue, I would be the first to throw my hands in the air and shout: Don't shoot! I am a civilian and (mathematically) unarmed!

please do. But I won't be reacting right away. I might need to study it first, and I will have to log off soon.

The following quote could be considered as the epitaph of the closed thread (The double slit experiment and superposition), as well as the leitmotiv of both this thread and the previous one (Interferometers and superposition). The quote is again of Maudlin, p.11. "The exact nature of the wave/particle duality of light need not detain us. We need only note two experimentally verifiable facts. First, light from certain sources has the effect of causing discrete, countable events in certain detection equipment. Second, if this light is passed through a polarizer, the resulting beam also behaves as if made up of photons..." He goes on to explain what he thinks is a mysterious behavior of the photons which, separated in space by a random distance, still react in a predictable way, but most importantly, in a correlated fashion to polarizing filters: "When the filters are aligned, in whatever direction, the photons are perfectly correlated: each does what the other does. If the filters are misaligned, then the photons still behave as if they have the same polarization. That is, suppose R passes through its polarizer, which is oriented in direction θ. Then L will act as if it is polarized in direction θ. If the left polarizer is also oriented in direction θ then L will pass, as we have seen. If the left polarizer is oriented at θ + 90° then L will be absorbed. And if the angle of misalignment θ is between 0° and 90° then L will pass the filter a proportion cos2 α of the time." The most astonishing though is not the behavior of the photons, which seems to me quite understandable, but the conviction with which Maudlin embraces the mystery: "These simple facts about pairs of photons emitted by calcium vapor are enough to destroy any theory according to which physical reality is local." p.13. Let us recall the main points. 1) Two photons created out of the same atom have the same polarization which they keep even after going each in its direction, opposite to that of their twin. 2) When going through a polarizer they exhibit the same behavior if both filters are aligned. Otherwise the angle of misalignment between both filters determine how the second photon will react. 3) the distance between them can be theoretically infinite. Before we go any further, we need to clarify the second point since it forms the crux of the whole argumentation. Here is how Maudlin explains it: "When the filters are aligned, in whatever direction, the photons are perfectly correlated: each does what the other does. If the filters are misaligned, then the photons still behave as if they have the same polarization. That is, suppose R passes through its polarizer, which is oriented in direction θ. Then L will act as if it is polarized in direction θ. If the left polarizer is also oriented in direction θ then L will pass, as we have seen. If the left polarizer is oriented at θ + 90° then L will be absorbed. And if the angle of misalignment θ is between 0° and 90° then L will pass the filter a proportion cos2 α of the time." Understood this way, the problem does not seem as hard if we assume that: 1) both photons start with the same polarization, 2) both filters are identical. In such a situation, we can say that the distance between both photons is totally irrelevant. What is important are the two identities I have just presented. Photon 2 and filter 2 can be considered as a local system in the sense that they could swap places with photon 1 and filter 1 without changing anything to the results of the experiment. In other words, what happens with photon 2 and filter 2 is what would happen with photon 1 and filter 2 locally!

Here is the case I will be analyzing, as described by Maudlin p.12 "When calcium vapor is exposed to lasers tuned to a certain frequency it fluoresces. As excited electrons in the atoms cascade down to their ground state they give off light. In particular, each atom emits a pair of photons which travel off in opposite directions. The polarization of the photons individually shows no preferred direction: for any randomly chosen direction θ the photons will pass a polarizer oriented in that direction half the time. But although the photons individually show no particular polarization, the pairs exhibit some striking correlations. Roughly, each member of a pair always acts as if it has the same polarization as its partner." The question will therefore be: how are both photons related in their behavior? Do we need hidden variables, local on non-local to explain the stunning correlations between both photons, or should we accept the idea that somehow both photons are linked through some mysterious property that can jump through space and time, whatever the distance between both photons? Here again, my pretensions will be modest and limited to this and similar examples. It is too soon to widen my claim to the whole domain of entanglement. Baby steps.

Non-locality has been a main issue between Relativity and Quantum since almost a century, even if Bohr has been considered all this time as the winner of his debate with Einstein. Von Neumann was the first not only to formalize quantic theory, but also to give a mathematical justification to Bohr's conviction that his (Copenhagen) interpretation of the empirical results of quantum physics was the only correct one. Bohm valiantly attempted to revitalize an old de Brolie theory and base his own interpretation on the idea of the pilot wave, a wave that transports particles, as an alternative to Bohr's approach. His theory opened the way to the possibility of hidden variables in the evaluation of quantic experiments, contradicting the conviction that physicists could only hope to achieve a probalistic knowledge of nature, because nature itself was based on probabilistic principles. Bohm therefore refused von Neumanns canonization of the Copenhagen interpretation, and saw himself partially vindicated a couple of decades later by Bell's analysis of hidden variables. I say partially because the conclusions Bell had attained, even if they asserted that von Neumann's mathematical defense was full of gaps, nevertheless confirmed the conclusion that no hidden variable could be thought of that would explain the statistical regularities acknowledged by the whole scientific community, including Einstein. What Bell did, is leave the door open to non-local hidden variables, which was of course a repudiation of Einstein's deepest convictions. To understand this, we need to know what is at stake without drowning in the technical details. Imagine two photons originating in the same atom, and being therefore, as far as everybody knows, identical, except that when one "turns" left, the other turns right, when leaving the mother ship. It turns out that whenever measurements are made of one, quantum theory predicts what the results would be of the measurements of the other one. If that was all, the problem would be trivial, and we would just say that both photons are identical except for the left and right start. The same measurements will naturally give the same results in both cases. The problem is of course much more complicated than that. Here is how. Let us take the way photons react to polarizers (I am using Tim Maudlin's "Quantum Non-Locality and Relativity", 2011, ch. 1 Bell’s Theorem: The Price of Locality). The astonishing result is the fact that however we turn the polarizing filter for one photon, we can predict, statistically, what the result will be of using a different angle for the second filter. A concrete example: If you turn a polarizing filter 30 degrees relative to its reference position, (whatever you choose it to be, as long as it is the same for both photons), and turn the second filter to 60 degrees, the difference being therefore 30 degrees, you will be able to predict that both electrons will pass the filter in a definite ratio: let us say that photon 1 will pass x times through the filter, and the other times it will be absorbed. The second photon then will pass the filter 3/4 of the times relative to photon 1. If the difference between both filters is 60 degrees, the ratio will become, say, 1/4. To make it even clearer, changing the position by, say, 20 degrees would change the percentage of photons passing through the first filter, but we would see the same change in ratio between both groups of electrons if we rotated the second filter 20 degrees relative to the first one! [I will come back to this crucial point later!] So, we could say that, in one way, the relation between both photons is deterministic, but also, and at the same time, probabilistic. Instead of a 100% ratio, we get different statistical regularities which nobody understands. The question that comes immediately to mind is whether it would not be possible to replace these statistics with old fashioned determinism. After all, maybe if we knew more, we would be able to predict accurately each state of the second photon once we know the state of the first one. As I said, everybody thought (except Einstein and friends), and at least for a while, that von Neumann had proven that that was out of the question. There was no way we could get more knowledge than we already had. Besides, Heisenberg's Principle clearly stated that the knowledge of one property meant the destruction of what we already knew of other properties. Knowing for instance the momentum of a particle excluded the knowledge of its location, and vice versa. The problem was, how can both photons react the same way, in the same ratios as predicted by quantum theory, even when they are miles apart as has been confirmed by many experiments. Here is how another author expresses it: "Suppose that two people are located far away, each of whom tosses coins and the results are always either heads or tails, randomly, but are the same for both throwers. Or suppose that in two casinos, again far away from each other, the roulette wheel always ends up on the red or black color, again randomly but always the same in both casinos. Or imagine twins far apart that behave exactly in the same fashion. In all these examples (and in many others that are easy to imagine) one would naturally assume (even if it sounded very surprising) that the two coin throwers or the casino owners were able to manipulate their apparently random results and had coordinated them in advance or that genetic determinism was much stronger than one usually thinks. Who would suppose that one coin tosser immediately affects the result of the other one, far away, or that the spinning of the ball in one casino affects the motion of the other ball, or that the action of one twin affects the behavior of the other twin? In all these cases, one would assume a locality hypothesis; denying it would sound even more surprising than whatever one would have to assume to explain those odd correlations. But one thing should be a truism, namely that those correlations pose a dilemma: either the results are coordinated in advance or there exists a nonlocal action." from What Did Bell Really Prove? By Jean Bricmont, ch.4 of QUANTUM NONLOCALITY AND REALITY 50 Years of Bell’s Theorem, by Mary Bell and Shan Gao (editors), 2016. And that is in fact, what Bell is supposed to have proven: local hidden variables are excluded, but non-local variables remain possible. I will not go into Bell's argumentation right now, and will just ask myself how I would solve the problem The above examples all concern macroscopic objects, and nobody doubts that causality is always local. The problem is with quantum objects. My claim will be that causality is always local, and that entanglement is the result of faulty logic and theoretical biases. For that I have to return to Maudlin's example of photons and polarization filters.

It is you who do not understand what the whole thread is about. I show that it is not necessary to assume superposition of particles. That is what you should concentrate on. Show that I am wrong in my claim. Show that my claim is wrong, instead of playing teacher.

If you had read Scariani, you would know that his book is not about wave-particle duality. Please stop trying to change the subject of my thread. I agree that both subjects are very closely related, but that does not mean that they are the same. I have first treated of double slit experiments exclusively and you were the one that kept hammering on the necessity of also treating MZi's. I have put my claim forward and made it abundantly clear that it was not incompatible with the wave-particle theory of light. The same holds for this thread. My claim is also not incompatible with the wave theory of light. If You made the effort of reading my posts you would see it immediately. here is a quote from my other thread: "I have claimed that this disappearance is a mere theoretical phenomenon, based on the belief that it is the only sensible explanation when one takes into account the dual nature, or at least the wave-theory of light.I would like to make it clear that my claim is not incompatible with this theory. The interference patterns may well be the result of constructive and destructive interference of particles moving together through the slits. They may even be the result of single particle interference.What is essential is the reason why they seem to disappear when "observed".

It is not about the wave-particle duality, reread the first post. First you thought it was about electronic gates, and now you think it is about wave-particle duality. Maybe you shouldn't work so hard, and go to bed early.

I am overwhelmed by your generosity. Would you be so kind as to answer my claim too with something else but generalities? I think your strategy is obvious. Keeping a meaningless discussion going as long as possible, to have the thread finally closed. This is my last reaction to anything you say that does not specifically concern the subject of the thread and the claim I have presented.