KFS

So dx/dt=2.67×10^(-7)y-10.67x, where y=(1-exp(-2.67×10^(-7)t)(2.51×10^6), is that correct? Or dx/dt=2.67×10^(-7)y-1,067×10^(-6)x? Yes I have done integrating factors. I have no problem solving these equations only setting up the problem.

Thanks for answer but how do I represent the amount of pollutant in the second lake as a differential equation? I understood the process in Example 4 but not with the information of both lakes in problem 15.

The problem I'm stuck is 15. I added Example 4 so you can see what problem 15 is all about. What I've been trying is: the amount of pollutant in the first lake is y=(1-e^(-2.67*10^(-7)t)(2.51*10^6). So I multiplied y by the rate entering the second lake which is the one leaving the first lake. Then I multiply 10.67 by the amount of pollutant in the second lake which is what I have to find through a linear first-order differential equation. Then I have dc/dt=10.67y+10.67c. Something's wrong but I don't know what. I do not need help solving this kind of differential equations where I need help is FINDING THE DIFFERENTIAL EQUATION TO SOLVE.

The problem says: The equation R(dQ/dt)+Q/C=E describes the charge Q on a capacitor, where R, C, and E are constants. (a) Find Q as a function of time if Q=0 at t=0. (b) How long does it take for Q to attain 99% of its limiting charge? I solved (a) and I got Q=-exp(-t/RC+ln(EC))+EC. But I don't know how to solve (b), I don't know what to equal Q to solve for t.

Okay I see it now. Thank you, I was stuck in this.

How did you get xy=sinh(x+y)?

The problem asks to find dy/dx in y=sinh(x+y)/xy=1. What I do is: differentiate both sides using implicit differentiation which gives d/dx(sinh(x+y)/xy)=0. I differentiate this setting y' where I have to differentiate y with respect to x. Thus I get (xycosh(x+y)+xyy'cosh(x+y)-ysinh(x+y)-xy'sinh(x+y))/(xy)^2. Then I solve for y' and I get y'=(-xycosh(x+y)+ysinh(x+y))/(xycosh(x+y)-xsinh(x+y)). But the answer in the book says y'=(y-cosh(x+y))/(cosh(x+y)-x). What am I doing wrong? Is my procedure incorrect? Thank you.

Is this correct?

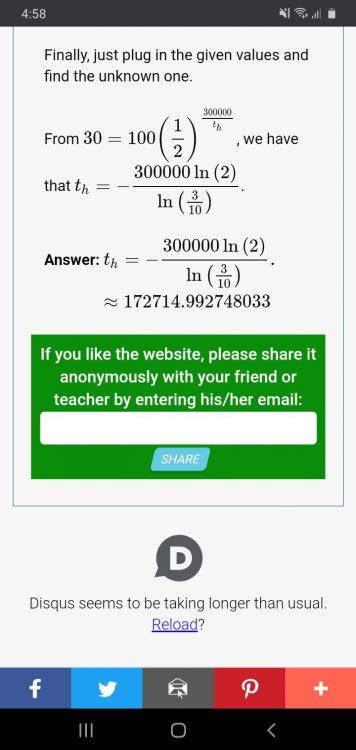
How did you get the 500,000?

The formula is f'=-(kappa)×f, where f=f(0)e^(-kappa×t), or (1/kappa)×ln2. In this case what would each term mean? I didn't understand that.

How do I do it then? Can you explain?

The problem says: It takes 300,000 years for a certain radioactive substance to decay to 30% of its original amount. What is its half-life? The result is 173,000 years, but I don't see how it is obtained. I tried solving for x in f(x)=300,000e^(300,000×x)=0.3, which is approximately x=0.00004. Then I solved for x in f(x)=e^(-0.00004×x)=1/2, which is approximately x=173286. That's the closest I got to the actual result. What am I doing wrong? How do I obtain 173,000? Or maybe my answer is correct and 173,000 it's just an approximation? Thanks.

Thanks for your help. I just wanted to stick to the book procedure but sometimes the book makes it harder than it really is, this has happened before.

In Example 3 and Example 4 what is the meaning of omega? Why is it 1 and 3 respectively? I don't know how these results are obtained. I differentiated the expression above Example 3 and filled in with the given information in Example 3 but it didn't make anything clear. Thanks.

Thanks, that's been helpful.

In Example 2, everything was fine, what I was doing matched perfectly with the book until the part "Setting this equal to zero gives *equation*". How is this? The expression on the left has no p, how can it have a p on the right? If the derivative dS/dx is set to 0 how is an x on the right, at the other side of =? I understand the rest. It's just that I don't see how one expression results in the other. That's all. Thank you. P.S: Sorry if images are annoying, english is not my first language, so this way it's easier for me to explain and for you to understand.

Thanks for the help. Yes, I am familiar with composition of functions and the chain rule. It's just that word problems are hard for me.

In Example 1: I don't understand the procedure of this exercise. I do know why the derivative of the angle with respect to time is 2π/30. What I don't understand is the rest. It says x=10tanθ, how is this possible? It gives me, and the computer, by tanθ=opposite/adjacent, x=10/tanθ, not 10tanθ. What I don't understand either is why both derivatives (dx/dθ) and (dθ/dt) are multiplying. Why is x=8 choosen? Why not any other number? Thanks for the help.

How do I find the sum of 1/(1+k^2) from k=1 to 1000? The book didn`t provide any information of how to solve rational sums, nor formulas for greater powers than 1. I have no idea how to do this. Thank you.

I just don't understand this. What's the process to get these answers? I tried the same process as with closed interval but I was wrong. Why none, none, none, none? I'm stuck. Show me how you would do it, or any other example you put to help me understand. Any help is welcome, thank you for your answers. (EXAMPLE 2, (b)).

Thank, mathematic.

Thank you,

Hello. This the problem: The population of Booneville increases at a rate of r(t)= (3.62)(1+0.8t^2) people per year, where t is the time in years from 1970. The population in 1976 was 726. What was is it in 1984? I' ve been trying integrating and then evaluating the integral at t=8 (8 years, 1984-1976=8). The answer must be 3195. I want to learn this because I saw the next problems in my textbook are similar to this one. It might be silly, but any help is welcome. Thank you.

Ok, thank you very much for the explanation. But 10 and 20 were not in the problem' statement, so where do they come from?