-
Posts
699 -
Joined
-
Last visited
-
Days Won
3
Content Type
Profiles
Forums
Events
Everything posted by taeto
-
I appreciate that, and agree with what you say here in your quote. It still irks me a little when you suggest that certain mathematical definitions are circular, when they are clearly not. It is kind of a tautology, since if any text purports to be a mathematical definition, and it is in ordinary use 'circular', then it could not be a mathematical definition at all. I still do not have an idea why you would suggest that the example of 'geometrical product' can be considered circular. But I suspect that a certain fact about it may present a clue. If I am right, then the word you are looking for in place of 'circular' might be 'incomplete'. I know a few things about how mathematics works, and I am very much a layperson when it comes to philosophy. I can well stand to be corrected as I proceed to say something 'philosophical' as follows. First, I suspect that you expect mathematical definitions to be largely of a different nature than definitions used in the outer world. I have in mind something like the following definition of 'a cat': It is something which (i) is an animal, (ii) has four legs, and (iii) has a tail. In the outer world it serves as a description of an object. In mathematics it would be a definition of the term 'cat', providing one is already familiar with the terms 'animal', 'leg', 'tail', as well as with the number four, as mathematical terms. For an example of an outer world cat, you may consult youtube, say by searching for 'lolcats'. For an example of a mathematical cat, we could let 'animal' be defined as an abstract group, a 'leg' an element of the group, and a 'tail' a neutral element of the group. In which case \(\mathbb{Z}_4,\) the cyclic group of order four, and the Klein \( 4\) -group \(\mathbb{Z}_2\times \mathbb{Z}_2\) are two examples of such mathematical cats. What is 'wrong' then with the definition (i)-(iii) in the outer world case, and in the mathematical case? Outer world case: We can assume, I hope, that the concepts of animals, legs and tails are already well-known, I hope, e.g. even chairs may have legs, and kites may have tails, but the meaning of the terms is clear. (a) there are objects (e.g. dogs) that satisfy the definition, yet they are not cats (\(\alpha\) error), or (b) it does not correctly capture the meaning of 'cat', since some actual cats are without tails (\(\beta\) error), or (c) it does not define any particular cat (\(\gamma\) error). such as my own pet cat, hence the definition is not complete, meaning that it does not define exactly that which I am interested in. Mathematical case: Again, the meaning of 'animal'=group and 'leg'=element and 'tail'=neutral element are assumed already known. We notice that outer world words are sometimes used for mathematical objects, without the meaning carrying over much. (a) An \(\alpha\) error does not occur, since every object that satisfies the definition of a 'cat', such as a dog, is a cat by definition. A dog may be called a dog-type cat, that is all. (b) A \(\beta\) error does not occur, because an object which does not satisfy the definition of a 'cat' is not a cat, by definition. (c) There is \(\gamma\) error, since there exist more than one (in fact exactly two) cat, which makes the definition of a cat incomplete. In conclusion, you seem to consider the case of \(\gamma\) error to qualify as 'circular'. But let me check again, because you told me to "define '2'". That was in the context of natural numbers, and so the request makes sense. The character/symbol '2' is used as a name for various objects in mathematics, such as the natural number 2, the rational number 2, the real number 2, the complex number 2, etc. I can offer this explanation of '2' in Peano Arithmetic: "the number two is the successor of the successor of the number zero". Does that seem to your satisfaction?
-
I do not understand any of that. But do you think that what you have now is useful to you, or have you got any additional questions? Just to make sure. Once you decide on assigning some value to \(t,\) like \(\pi/6, \pi/4, \pi/3\) or any other value, then we can calculate \(\sin t\) and \(\cos t\) just in the same way that we are used to?
-
I do not understand what you mean. If you set \(t = \pi /6\) in your equation, then we can (if we are lucky) solve the equation and find a solution \(a = a(\pi/6).\) If we set \(t = \pi/3\) we may also find a solution \(a = a(\pi/3)\) to the same equation. It is extremely unlikely that we will discover that \(a(\pi/6) = a(\pi/3)\) holds. I worry when you say that \(\sin(a)\) and \(\cos(a)\) are "unknown" and "can be defined". Once we have \(a,\) then normally they should be completely known and determined by calculation of the function values of \(\sin\) and \(\cos\) with argument \(a.\)
-
If this answers your question, then fine. All I was saying is that if you keep your \(a\) constant, then the point \((0,y)\) depends on the value of \(t.\)
-
If your notion of `circular' only means that in the definition of one concept there is reference to another concept, then your notion differs from the usual understanding. You can choose to stick with your own private understanding. But it will make communication difficult.
-
Since you started out by mentioning how numbers are defined, I assume that you are already familiar with Peano's axioms: en.wikipedia.org/wiki/Peano_axioms I also assume that you now agree that nothing is circular in your geometric example.
-
I am pretty sure you are reading it wrong. The formula (3) is not a definition of anything; it is an identity that follows from the previous definitions of geometric and inner and outer products. It is similar to first defining what you mean by '2', '+' and '4', and then deriving the identity '2+2=4' from those definitions. In fact adding (3) as a definition would not make anything circular anyway, since it is just an easy consequence of the previous conditions given for the products.
-
Thank you for giving an answer +1. But the page that you linked does not define the geometric product using the inner or outer product, so far as I can see, since the four listed properties of the geometric product do not contain any expression with a \(\cdot\) in it. Can you point to the line of text where you think this happens? I would agree if you argue that the definition is incorrect. It allows \( a\cdot b = 0\) for all vectors \(a,b,\) which is likely not intended. Even that does not make it circular. Edit: Forget the last paragraph, I missed that it says that \(|a|\) must be positive, so nonzero. So the thing is only incorrect in saying that \(|0|\) has to be positive.
-
What is wrong with solving problems by computation? After all it is what people tend to do these days. Maybe it also helps to know if and where you have possibly seen an actual mathematical definition that is circular?
-

Can matrix element be multiplication of two matrices
taeto replied to kemfys's topic in Linear Algebra and Group Theory
Hi kemfys, actually that is exactly what a ring means. It is possible to add elements, and the addition is commutative. It is possible to multiply elements, but the product is not necessarily commutative. Matrices over fields like \(\mathbb{Q},\) \(\mathbb{R},\) and \(\mathbb{C},\) are examples of rings. To say that a matrix is "over a field" means that all the entries of the matrix belong to this field. In the case of a \(2\times 2\) matrix this would be all four entries. Matrices over a commutative ring like \(\mathbb{Z}\) still form a ring themselves. I think that I get that you want to consider matrices over rings that are not necessarily fields, or even commutative rings like \(\mathbb{Z}.\) Maybe you should simply work through some examples to experience how it works. It seems that if you have \(2\times 2\) matrices \(x\) and \(y\) as variables and you require your matrix \(P\) to equal the matrix \(Q,\) then it leaves you with four equations (expressions that should be equal to \(a,b,c,d\)) in eight unknowns (the entries of the matrices \(x\) and \(y\)). In the general case the answer should be yes, you can find a solution. Though usually the complete solution consists in a 4-dimensional solution space. -
Not sure if we are doing this and just being kept in suspense. I like optimization problems. Rather, from having to teach calculus to engineering students, I am no longer all too bothered by them. So I came up with a puzzle. Say we have M moles of electrons and want to pack all of them into a ball-shaped container of radius R, and there should not be anything in it than just electrons pure. Disregarding the amount of energy needed to assemble the electrons, which is a standard exercise to calculate, what would be the optimal choice of material to use for the container itself, also from an energy standpoint? That is, to construct a container able to contain one mole of electrons within a proton radius ought to be fairly energy consuming. Whereas to contain the electrons within the radius of the observable universe should be a piece of cake.Well, not inside our own observable universe, since we do not want to have to first clear out all the stuff that is here; so we just do it somewhere else.
-

Can matrix element be multiplication of two matrices
taeto replied to kemfys's topic in Linear Algebra and Group Theory
It is given that \(b\) and \(c\) are not equal? From which ring(?) do you take your \(x\) and \(y,\) and how is \(x \otimes y\) defined? Do \(x\) and \(y\) have to be \(2 \times 2\) matrices? -
It seems we agree on this, or at least something very close to it. To simplify more, it could be useful to introduce (in your notation) b = Pi/2 - a. Either way this is a function of t which is not constant. As t grows, the point (0,y) moves upwards on the y-axis.
-
I cannot reproduce the LaTeX problem.
-
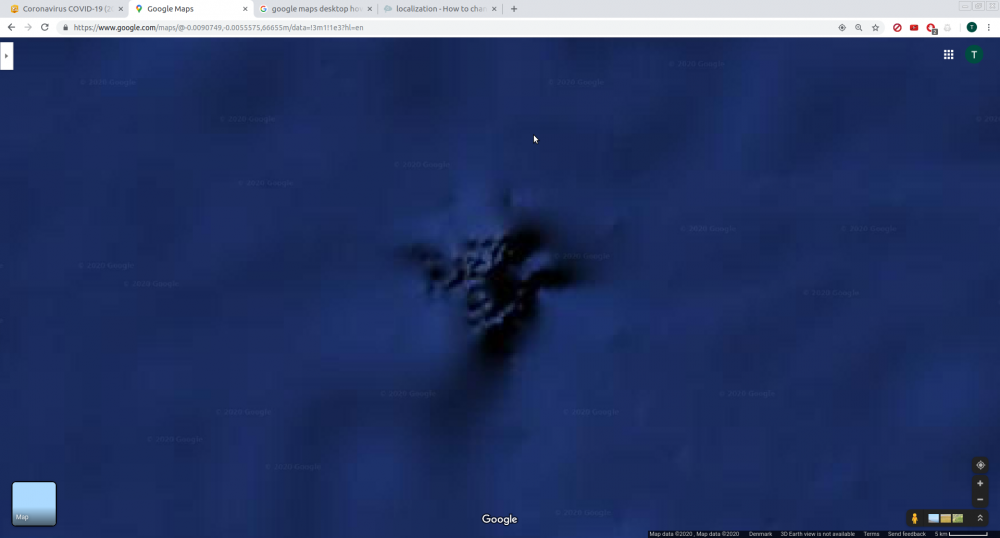
It is just another mountain, a little closer to the surface than normal. And very close to the intersection of Greenwich and the Equator. The numerologists ought to be attracted to it like (insert favorite disgusting insects) to (insert excretion by favorite domestic animal). Does it look volcanic, so that it might have been an actual island previously? St. Matthew Island?
-
I see lots of underwater mountains in the same extended region of the Atlantic. Seen from satellite they all look different from this one. Not similar.
-
True, it is close to (0,0). I looked at that already. Clicking on the map gives -0.004955, -0.023410. The blob should probably not be there, but it represents cases that belong randomly elsewhere on the globe. The satellite however, why should satellite data be collected in a fashion so that pixels from other places get thrown into this location? On the other hand, if it is a genuine geological feature, it seems rather unique.
-
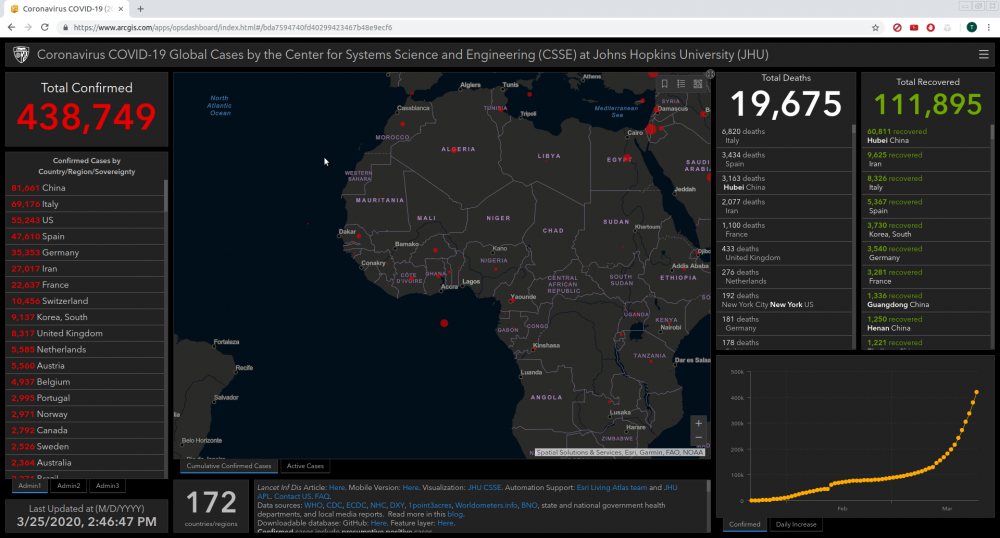
I noticed on the Johns Hopkins map of the Covid-19 outbreak a big blob off of the west coast of Africa. Not sure what to make of it, I took a look at Google Maps to see if there is any populated island located south of Accra and west of Gabon just outside the bay of Guinea. But the map shows no land area. However there is a kind of unusual structure apparently not far below water surface in this location. In the first of the below satellite shots it is only a little cross shape. Magnification shows an uncharacteristic looking feature about 2x2 kilometers in size.
-
This is shaping up to become one of the biggest conspiracy plots of this decade.
-

Corona virus general questions mega thread
taeto replied to FishandChips's topic in Microbiology and Immunology
I cannot find it either. Anyway, it means what it means 😂 -
I think that I begin to accept that this is physics-math speech and not mathematics speech. It does not mean that I understand much. I know of Hausdorff dimension, which may be non-integral. I do not know what you mean by a 'tube' exactly, but I can imagine a topological definition of an infinite tube, though not one that satisfies the dimensional requirement, so that part alone is exciting. But skipping over that, I know the term 'Planck length' and the concept of 'radius', but I have never heard of the 'Planck radius'. Did you invent this notion?
-

Corona virus general questions mega thread
taeto replied to FishandChips's topic in Microbiology and Immunology
Sorry to be a stickler for wanting to know what words mean 😉. -

Corona virus general questions mega thread
taeto replied to FishandChips's topic in Microbiology and Immunology
Thanks a lot Kart! Ah, so I see the term is 'viable', not 'alive'. A typing exercise for a new intern perhaps 🤔. -

Corona virus general questions mega thread
taeto replied to FishandChips's topic in Microbiology and Immunology
Very curious about the title of that link. So the virus lives for a while, then it dies? When is it pronounced dead? After losing an envelope? Or its own capsid? What kind of 'air particle' does it inhabit? Does it need protective cover, or is it possibly just its own 'air particle' like a tiny dust grain? Similar questions for 'living on a (hard) surface'. -
That is a lot. Did you say earlier that we can throw in dark matter as well? I have not studied any of this yet, so is there any particular paper that you can recommend as a starter, preferably in which one of these explanations/predictions gets proved in full or a proof gets outlined?