quiet

So we do not know Maxwell's inner conviction a little before his 48 years. We only know that at one stage of the investigation he decided to abandon the mechanical model. --------- Imponderable. Thanks for bringing this word. In Spanish it also exists, it is written the same and means the same. The texts in Spanish also apply to the ether that adjective. Now that you have explained the use in English, with the annexes and in the context of physics, I will be able to improve the expression in the future. Thank you. The one proposed hundreds of years ago and eliminated in 1905.

For classroom, and for improve my cultural panorama, your contribution is valuable (and beautyful). Thak you very much. --------- Respect to Maxwell himself. Have Maxwell believed until the tomb in the neccesity of a substantial medium that allow the electromagnetic propagation? Maxwell begin using his mechanical model and, in last stage of his research, he have discarded that model and keep only the set of equations, wich include the electric displacement. Have Maxwell ignored the conflictive situation between the rigidity and the evanescent density are needed to formulate the phenomenon in ether terms? Can a person who have created such delicate, datailed and versatile mechanical model ignore the bugs of it?

I don't know how clear was my initial post for who read that I have wrote. For me can mean something and for other person can mean something very different. Now I will try to improve the expression. I have reasons, physical and mathematical, to reject the idea of ether. Mathematical reasons are exposed in this thread. I have reasons but, anyway, I am interested in all kinds of arguments. Why? Because I am a teacher. There are a little number of boys and girls really interested in this issue, and they are very intelligent, and they present many valuable arguments. I am trying to collect in the forum powerful arguments of all kinds, that can prepare me to manage better classroom arguments. When I started the thread, I ignore that it can generate passioned discussion and fighting. And I ignore that I will need to fight too for achieve that people read my posts with a bit of attention, in a way that avoid missunderstanding. I don't wrote, in no paragraph, that I am in favor of the ether hypotheses. But some persons have believed the inverse idea. Anyway, here was generated a very interesting development of the main issue. And I am greatful for this.

If you have read my posts carefully at this thread, you will have understood that I have never tried to argue in favor of the ether. And you will have noticed that mathematically I have argued against, because the vacuum is polarizable and the polarization fulfills everything that can be asked of a substrate. I do not try to discuss something outside the main thread. And I have already mathematically shown the minimum to give a framework to the subject.

Why in a group of people interested in science prevails the spirit of dispute, instead of the spirit of understanding? It gives the feeling, in many cases, of people who read the notes of others only to trace reprehensible phrases. In many cases, they cut sentences without having read or understood the context, to write a sour repudiation, very far from lucid discernment. So we hope to advance every little bit more in the understanding of the topics that we like the most? Let's take an example in my case, so as not to involve someone who does not want to be involved. Did someone take the task to read my first post carefully, understand the content cleanly, then go to the second post, do the same and, thus, get to my last post, to have a conceptual and contextual panorama representative of what I am exposing? If someone had done this work, no one would appear saying that my intention is to affirm the existence of the ether, nor would people appear writing pieces of history to, supposedly, help me understand why the ether is unnecessary. No one has seen that I took the task of putting mathematically the reason why neither the ether nor anything of that kind is necessary. This thread is only one of the threads spoiled by the vocation of dispute, which replaces the vocation of analysis and understanding. I trust that after reflecting every person within himself, this unfortunate problem will disappear.

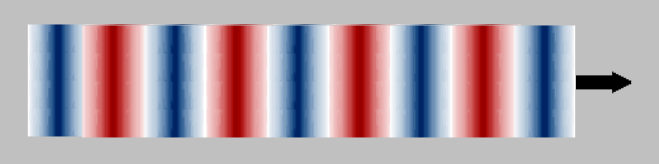
Dear studiot, for the first time I find a person who exposes justly the essentials in this subject. What you have written has mathematical expression in the following. In dissertation format it would be a long and confusing paragraph. Then I prefer a dialogue format. - Environment: The vacuum - Theoretical context: Classical electrodynamics - Starting point: The electromagnetic wave equation - Highlight detail: In the propagation, the electric displacement works undulatory. That is, that operation fulfills some solution of the wave equation. - Mathematically there is a complex exponential solution. For now let's not think about physics. Think only of mathematics. - This solution may correspond to circular or elliptical polarization, with both components in transverse direction. It may also correspond to the case of a transversal component and a longitudinal component. Remember, momentarily we are not thinking about physics. Only in mathematics. - Now we start thinking about physics. - In the vacuum, the electric field E can not have a longitudinal component, since there is no free charge in the vacuum. - Something prohibits that there is some type of linked charge in a vacuum, even if it is a type that has not been treated or known until today? - Although it would be a very conditioned type of bound charge, its existence is not prohibited. It should meet conditions that we have not faced before, but existence is not prohibited. - Any special condition that serves as an example? At each point the charge density should vary locally by alternating signs, with no charge movement in the direction of propagation, since the charge movement is conduction current and, in a vacuum, only the displacement current is allowed. - Mathematically exist the complex exponential solution. Is there any field in classical electrodynamics that can, without conflicts, fulfill that solution without having both transverse components? - Yes, the electric displacement. [math]\vec{D} = \vec{P}+ \varepsilon_o \ \vec{E}[/math] - Could the vector P be transverse? Impossible. Polarization is a field that, in terms of local results, has collinear symmetry. To have collinear symmetry we need that there can be, in a finite region, two resultants that have the same module, they are on the same line and they have opposite senses corresponding to the opposite signs of the bound charges. In the case of the wave, two vectors P corresponding to different charging signs are in different half cycles. In case of being transverse vectors P, the collinear symmetry is impossible. Then the only possibility is that P is longitudinal. - In the case of a plane wave, without circular or elliptical polarization, when the direction of propagation is the axis x , we can express the displacement in the following way. [math]\vec{D} = \vec{x} \ P + \vec{y} \ \varepsilon_o \ E[/math] - The solution of the wave equation in that case has the following form. [math]\vec{D} = \vec{x} \ \hat{D} \ cos\left(\omega t-kx) \right) + \vec{y} \ \varepsilon_o \ sin\left(\omega t-kx) \right)[/math] - And the modules meet the following condition. \hat{D}=\hat{P}=\varepsilon_o \ \hat{E} - In that solution, divergence of the electric displacement is not equal to zero. It is finite. Then there is a finite bound charge density in the region where the wave propagates. After the passage of the wave, when nothing propagates in the region, the bound charge density returns to zero. The road disappears after the passage of the train and, so that the train can travel, the road is formed only where the train is at each moment. - The road does not travel. Locally, a piece of road is born at each point where the train has to pass. In other words, the bound charge does not travel. The infinitesimal bound charge that allows the propagation appears locally at each point. At each point the bound charge density is finite and varies sinusoidally, in the case of a sine wave. Actually @studiot, the example you have given corresponds perfectly to a solution accepted by classical electrodynamics. Let to see how looks the divergence. [math]\nabla \cdot \vec{D} = \hat{D} \ k \ sin\left( \omega t - kx \right)[/math] Does that mean that some charge travels in a vacuum when the wave propagates? No charge needs to travel to produce that divergence. In the cities there are giant illuminated signs, which are panels populated by thousands of luminous cells, controlled by a programmable device. A program can achieve that the brightness of each cell varies sinusoidally, in the form corresponding to a wave function. You can program two colors, say blue and red. The first cell is initially dark. Then the blue light grows sinusoidally, reaches the maximum and decreases sinusoidally, until the cell becomes dark. Follow the sinusoidal stage of the red light, which does the same. All the cells are immobile on the board, but the program manages to see alternate blue and red areas traveling along the board. The effect is equivalent to colors in movement. At each point of the vacuum, the charge density varies sinusoidally. The signs of the charge do the same as the colors. The effect is equivalent to alternating zones with opposite charges traveling in the direction of propagation, although no infinitesimal or finite charge is actually moving. - Although the charge does not really move, the effect is equivalent to moving charge, as happens with colors that look like moving sections with [math]\tfrac{1}{2} \ \lambda[/math] in blue and [math]\tfrac{1}{2} \ \lambda[/math] in red. - The effects of the virtual movement of the charge density are equivalent to a virtual density of current in the direction of propagation, equal and opposite to the longitudinal component of [math]\dfrac{\partial \vec{D}}{\partial t}[/math] . This derivative is part of the Ampere-Maxwell law. Ampere-Maxwell law [math]\rightarrow \ \ \ \vec{\nabla} \times \vec{H}=\vec{j}+ \dfrac{\partial \vec{D}}{\partial t}[/math] . Finally [math]\vec{\nabla} \times \vec{H}[/math] it remains, in a net form, identical to the result obtained for the real solutions of the wave equation, which lack a longitudinal component.

@MigL Thanks for what you have contributed. What is the KISS Principle? --------- I return to the basic theme of the thread. The bicycle without wheels does not travel. And the concept of physical wave does not apply when the substrate is missing. Here are two details that merit clarification. Substrate properties? 1. Be present in all points of the region where the wave propagates. 2. The state of the substrate at each point is perfectly defined for each moment. I repeat Without substrate there is no physical wave. You can, if you wish, formulate a formally similar function, or if you want identical, a wave function. Without substrate, such a function does not correspond to a physical wave. --------- Let's put the pieces of the puzzle on the table. - In all tests the electromagnetic radiation gives the signals that are expected from the waves. - These same proofs prove convincingly the impossibility of a substratum of substantial type, as implied by the idea of the ether. There is only propagation and emptiness. - Without a substrate there is no wave. --------- Let's try to put the puzzle together. - Substrate = Substance is the hypothesis rejected by the evidence. - Propagation and emptiness is the scenario exhibited by the evidence. - The substrate is essential for the existence of the wave. - In a scenario where there is only propagation and vacuum, is there something capable of fulfilling the function of the substrate? This is like saying that there are only two people, Mary and John, it is known that one has clear eyes and it is known that John has dark eyes. Who is the person with clear eyes? In the case that interests us, the propagation is the effect of the substrate, that is, it is not the substrate. Then the only thing that the function of the substrate can fulfill is the vacuum. Can the vacuum really operate as a substrate? This question is too crucial to answer verbally. We need mathematical language. Which 19th century theory offers a complete, coherent and consistent description of the spread in a vacuum? It's Maxwell's electrodynamics. Now comes the most delicate stage of the puzzle, because our subjectivity lurks to bias the range of what should be investigated. The electromagnetic wave equation has a complex exponential solution. Subjectively we assume that, in a vacuum, that solution can only correspond to circular polarization, elliptical, or cases of that type. Without attempting a meticulous and careful mathematical development, we assume that, in a vacuum, the exponential solution can not correspond to a flat wave without circular or elliptical polarization. Before stating something like this verbally, we need to examine that in the context of Maxwellian electrodynamics, a pertinent theory in the 19th century. When we make the mathematical statement, all the following appears. - The classical electrodynamics is perfectly prepared to formulate the polarization of the vacuum. - A vacuum unable to polarize would not serve as a substrate. In contrast, the polarizable vacuum serves perfectly, because it generates a density of bounded charge in the region where the wave propagates. That charge density is a continuous function defined throughout the region. Is that possible ? The usual particles can not establish a perfectly continuous charge density, that is, continuous in infinitesimal terms. And here another prejudice interposes, because we believe that the electric charge can only appear in the format of the usual particles. Something worse. We imagine that the quantization of the charge and the perfect continuity in the region of propagation are mutually incompatible. That is a mistake and classical electrodynamics explains why. - The idea of the ether is inadmissible. The polarization of the vacuum is admissible and essential in the context of classical electrodynamics, since this polarization perfectly fulfills the function of the substrate. It fulfills physically and mathematically.

@studiot So we have a ring of conductive material eg a hoop of wire? Yes. This ring is charged to a value of -2q, where q is much larger than the charge on one electron. So it is not electrically neutral then disconnected from the source of charge but insulated from the rest of the universe? Yes. The ring is then rotated with some (steady ?) velocity v ? Yes. Why should this scenario result in a magnetic field? A ring that has an electric charge and rotates is equivalent to a current loop. Are you trying to experiment with homopolar motors and generators AKA a Faraday Disk? It is not my intention. In case of similarity, I have not looked for that. --------- I have not been able to edit a previous post to add a data. So in this post I copy the content again and add what was missing. --------- I am thinking about a classical case, whose diameter can be, for example, 2.5 m. I choose this diameter because I want introduce later the case of two cylinders, wich differ a bit in diameter, have the same rotation axis (one cylinder placed into the other, like a cylindrical capacitor). The inner cylinder is in rest respect to the observer. Between both cylinders there are a radial electric field and an axial magnetic field. These fields are mutually perpendicular. Then, the Poynting vector that both form is tangent to the circumferece (sorry if language errors). There is a movement of EM energy around the circumference. Can this movement of EM energy remain in uniform angular distribution? Or a wave is formed between both cylinders? The region between cylinders have a contour, not equal to a waveguide, but able to reflect elemental waves and stablish waves groups. Waves groups naturally exhibit quantization. I do'nt know all details implied in this case.

@studiot I am thinking about a classical case, whose diameter can be, for example, 2.5 m. I choose this diameter because I want introduce later the case of two cylinders, wich differ a bit in diameter, have the same rotation axis (one cylinder placed into the other, like a cylindrical capacitor). Between both cylinders there are a radial electric field and an axial magnetic field. These fields are mutually perpendicular. Then, the Poynting vector that both form is tangent to the circumferece (sorry if language errors). There is a movement of EM energy around the circumference. Can this movement of EM energy remain in uniform angular distribution? Or a wave is formed between both cylinders? The region between cylinders have a contour, not equal to a waveguide, but able to reflect elemental waves and stablish waves groups. Waves groups naturally exhibit quantization. I do'nt know all details implied in this case.

@strange @swansont Very clear and helpful your answers. Thanks! --------- Are we all admitting that an electrically neutral system can have an effective magnetic field? Of course, magnetic stones are neutral systems and have effective magnetic field. Anyway, the atomic and molecular configuration of a stone differs quite respect two rings. Or not?

@strange @studiot Thanks for your contributions. This is the kind of reflections that I expected. Language issue: Thanks studiot for help me (more than once). Century! OK. Haha... French! May be excess of de Broglie's books?

@strange Uniform charge density in all rings. @swansont Its true. It is not the same total effect. Can be the same magnetic field in both cases?

@strange The reasons that lead the 19th siecle physycists to finally reject the idea of ether are in the pertinent bibliography. Were not correct to say, more than 150 years later, "oh, very fool the 19th siecle people, because there is a lot of reasons and a lot of evidences respect to the foolishness of that idea". This make no sense. What make sense is a comparison between the set of reasons we have today to reject it, and the sets of reasons in 19 siecle, one set to agree with the idea of ether, other set to reject it. And, within those primitive context, to recognize how and why the wright ideas go step by step emerging and achieving more and more consensus.

This thread come and go between good contribtions and fighting words that no thing contribute. I am greatful with the the contributive attitude, wich is evident in many posts. If someone want to continue fighting, go freely to that. I am not interested in that. Best regards.

@strange, your last post have the class of content that really work for me. Thank you. +1 Only one question. Have I wrote in any paragraph something tending to restablish the idea of ether? Agree respect to place this thread in history section.

Thank you. It's the kind of response that really works for what I need. Kaluza and Klein added a curved fifth dimension, of limited size and small scale. In 11 dimensions, the 7 extra dimensions are all small scale?

Dear members of the forum. Use this thread as a battlefield for a dispute? We had started well. We can continue well. --------- Let's not transform scienceforums into teasing forums. When I ask, I do it seriously. For example. Why is ether not necessary? Then we take the theorems of vector analysis and see mutual rotors regenerating fields in successive places that configure the advance in the direction of propagation. Very happy I say that ether is unnecessary because I have mutual rotors that do the job. My happiness is an epistemological abuse of the worst. Mathematics does not physically explain why ether is unnecessary. Admit that the cause is not the ether, it implies finding something physical that operates as an underlying cause. If the lid of the pot does not jump for a demon that was locked and burned with heat, then you have to find something physical that causes the cap to jump. Mathematics describes behavior. Behavior of something? Yes. Of something that physically exists. And teasing does not diminish epistemological abuse. Do not increase it. Teasing is, at best, a resource that dilutes the axis of the thread in a gap of distraction.

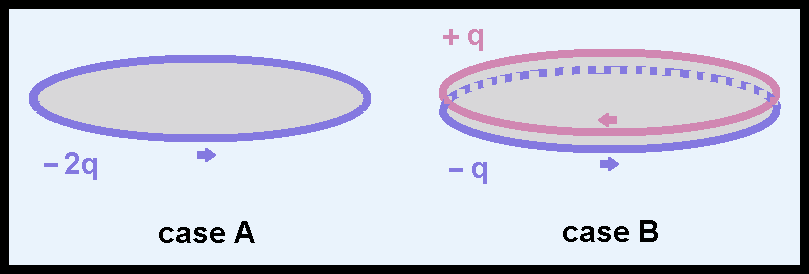
In case B, the net charge is equal to zero. That does not mean absence of charge. Rings with opposite sign charges, rotating in opposite directions, produce currents of the same direction and produce components of magnetic field that add up, to give in this case a net magnetic field equal to the field of case A. That is the idea. Well up there?

All people have offered answers of the kind I'm looking for. I appreciate that. Obviously, everything that can be added will complement the great historical lines. And some personal vision would be a wonderful possibility. I do not mean the word personal to expose a speculative idea. I refer that to an exhibition that invites reflection with an original didactic.

Case A: Ring with charge -2q turns and produces a magnetic field. Case B: A ring with charge -q rotates in the same direction as the ring in the previous case. A parallel ring with charge + q rotates in the opposite direction. Let's suppose that the rings are very thin and are very close together. Ideally we would say extremely thin and extremely close together. The angular velocity has the same modulus in all the rings. If I assume that the axes of rotation are all at rest relative to the observer and that Ampere's law is valid in both cases, then the magnetic field observed in case A and the magnetic field observed in case B are the same. Am I doing well here? I doubt because I am affirming the following. For the observer who sees the three axes at rest, two systems that have different configurations produce the same effect. I can not believe that the only effect of case B is to produce a magnetic (or electromagnetic) field equal to the field of case A. The difference in configuration should manifest itself in some effect. To say some effect is to say that I do not limit the possibilities to a magnetic or electromagnetic effect. An effect of another nature would also manifest the difference between both cases. Case B is perfectly symmetrical. Case A is asymmetric in comparison with case A. Opinions, reasonings, hypotheses? Useful ideas to mathematically analyze something?

I would like to collect reasons to discard the idea of ether. If there are reasons not to dismiss that idea, I would also like to collect that.

Some systems have the following property. When you deliver energy to the system, the system initiates an oscillation that has a characteristic frequency. This frequency does not depend on what you do to provide the energy. It only depends on the constitution of the system. This is how they behave, for example, a mass / spring system, a parallel LC circuit, a piano string with the structure that holds it tense, a pendulum. Mass / spring [math] \rightarrow [/math] You can gently take the dough and make a movement that stretches the spring, you can shake the table that holds the system, you can aim a fan to cause some movement, whatever you want. You will always observe the same frequency of oscillation. Parallel LC circuit [math] \rightarrow [/math] You can take a battery and make a spark at the terminals of the circuit, you can take a magnet and move it close to the coil. The oscillation frequency is always the same. Piano string [math] \rightarrow [/math] You can press the key that moves the hammer and hits the string, you can lift the top of the piano and hook the string with your fingernail, you can rub the string. The frequency, that is, the note, is always the same. Pendulum [math] \rightarrow [/math] You can take the weight with your hand and move it, if the weight is ferrous you can zoom in on a magnet and cause movement, you can aim a fan, whatever you want. The pendulum will always oscillate with the same frequency. That's why pendulum clocks have been pretty good. You have asked about a signal. Example, emitting radio waves. It is true that in the emission you are delivering energy to the space that surrounds you. And in this case, space is not responsible for always establishing waves of the same frequency, regardless of what you do. It's the other way around. The frequency of the broadcast depends on what you do. If your mode of emitting is to shake a magnet, the rhythm of your hand establishes the frequency, not the space through which the emission propagates. The same if you shake an electric charge. And if you use a transmitter device of the usual type, the frequency depends on how you control the transmitter, it does not depend on the surrounding space.

Very interesting property. Thank you. Thanks. This motivates another question. Are a cylindrical surface (with a sharp contour) and a smooth surface (without sharp contour) topologically equivalent?

Thanks for point out this. Very interesting phenomenon.

Help me please understand the obviousness.