-
Posts
569 -
Joined
-
Last visited
-
Days Won
1
Content Type
Profiles
Forums
Events
Everything posted by Kartazion
-
There is an unusual term called "QCD axion dark matter". Do you have any idea what "QCD axion dark matter" is? Here are among others the most recent documents on this subject: https://arxiv.org/abs/1910.04163 QCD Axion Dark Matter from a Late Time Phase Transition https://arxiv.org/abs/1905.04686 A Unique Multi-Messenger Signal of QCD Axion Dark Matter https://arxiv.org/abs/1901.07401 A new experimental approach to probe QCD axion dark matter in the mass range above 40μμeV https://arxiv.org/abs/1711.10486 QCD Axion Dark Matter with a Small Decay Constant
-

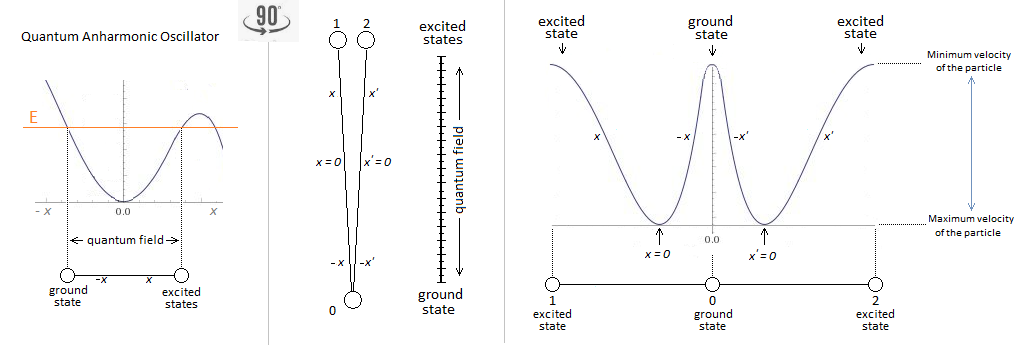
Associate a Harmonic Oscillator with the Functioning of the Universe
Kartazion replied to Kartazion's topic in Speculations
It comes from the work of a researcher. Even beginners like me. Is math compulsory? It was my question. It was because more younger I had to write oscillator 1001 times, before understanding that it took two l. -
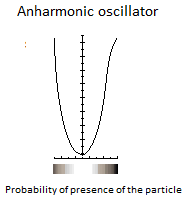
I want to make the link between a harmonic oscillator, and the functioning of the universe. Here, graphically speaking, this is how would be the evolution of the universe following the rules of the potential energy of a harmonic oscillator: What do you think of this evolution? Reference: [1] The Universe as an Oscillator https://arxiv.org/abs/1807.03864
-
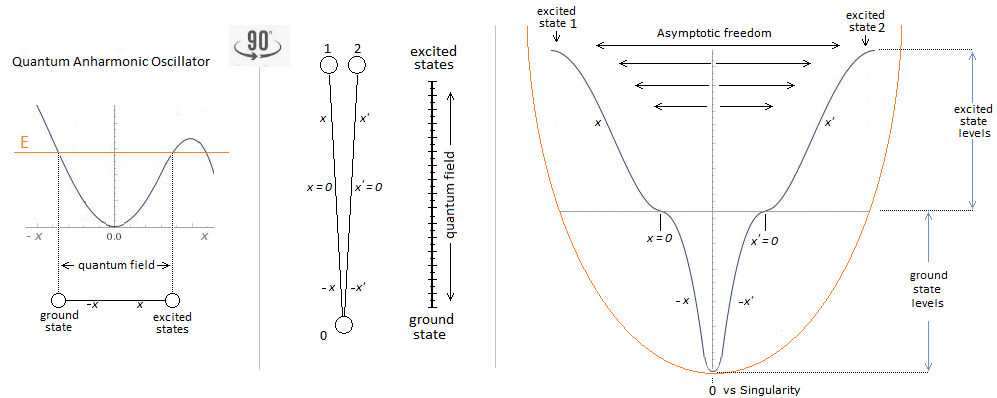
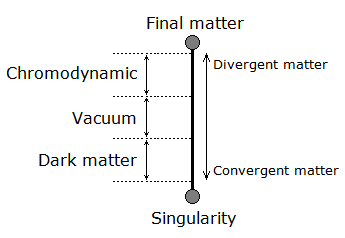
From a conference by Gilles Cohen-Tannoudji. I have a digital archive in French if necessary. The diagram comes from me. Indeed according to the principle of the anharmonic oscillator with which I work, I wish to claim that the particle oscillates between singularity and corelated matter. Between two is the flow of the particle which is only the quantum vacuum. The speed of the particle according to the potential energy. Dark matter is then only an addition of all the quantum vacuum space to a smaller area. This area can be reduced and reach a higher density. This could be compared to condensed matter. I do not know yet. Here is what I found: https://en.wikipedia.org/wiki/Weak_convergence_(Hilbert_space)
-
"Dark matter can be explained by the quantum vacuum of quantum chromodynamics" Gilles Cohen-Tannoudji. Here is the path taken by the particle between singularity and final matter: In the case of this deduction and reasoning, the dark matter must be expressed only with a particle at very high speed. Dark matter is only an addition of the convergence of the quantum vacuum at a point (an area). The density of dark matter is proportional to the convergence of space towards this singularity. Reference: https://www.scienceforums.net/topic/120416-anharmonic-oscillator/ https://www.scienceforums.net/topic/120749-quantum-chromodynamics-with-a-single-particle-in-motion/
-
Before arriving at the PDE, the probability distribution that I want as a function of point x and time t0 would have the following form: [math] P(x,t_0) = \delta(x-f(t)) \delta(t_0-t) [/math] Where [math]\delta(z)[/math] is the Dirac delta function. With this distribution, we can know the probability of finding the particle between the points x1 and x2, and in the time interval (t1, t2) in an analogous manner: [math] P(x_1 < x < x_2, t_1 < t < t_2) = \int_{x_1}^{x_2}\int_{t_1}^{t_2}P(x,t)dxdt [/math]
-
... Here is the part I was advised to study in order to be able to develop a probable mathematical solution to the given problem (which is, and with the help of an anharmonic oscillator, to highlight the duplication of a single particle, in two distinct points). Those are the Partial Differential Equations. I'll be back in a little while to give you the first forms of scripture. Thanks.
-

An Alternative Equation for the Wavefunction and its Eigenfunctions
Kartazion replied to John Henke's topic in Speculations
Planck ? -
Then ignored me, and don't answer. I was talking to StringJunky. I didn't know going to college or university was dangerous.
-
I have all my life to learn.
-
And I thought there was one thing more important than the other.
-
"Imagination is more important than knowledge. For knowledge is limited, whereas imagination embraces the entire world, stimulating progress, giving birth to evolution." Albert Einstein
- 276 replies
-
-1
-
“The only thing I know, is that I know nothing.” Socrates.
-
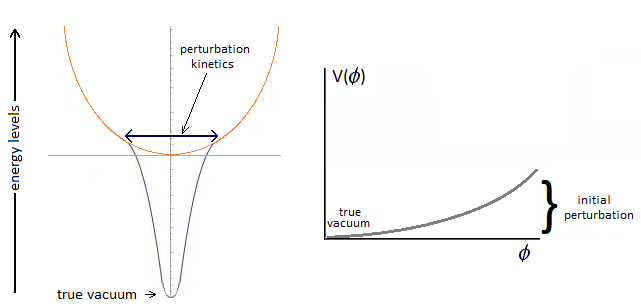
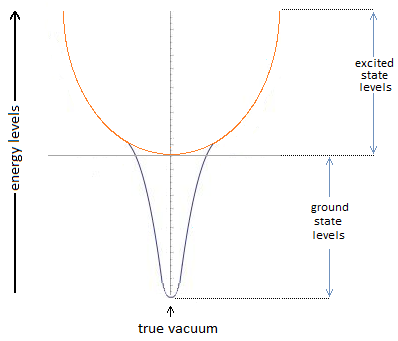
Only the extension of the energy under the well. From the false to the true vacuum. Conventionally this pattern is in a cascade, followed by a potential barrier. My idea is that there is a particle size slit. Either in the center, or two extremities not far from the center. Depending on the kinetic force, the particle may or may not pass through the slit to finally change the well. I'm not sure it works very well. Because the particle has to hit the chamfer at each pass. I have now learned the lesson.
-
I made a mistake. And I do not know if my reasoning is correct, especially in the case of a classical oscillator. Here is the explanation of my nonsense: I was based on the quantum perturbation of the ground state. Indeed by the energy of the disturbance and the oscillation of the flow at the bottom of the well, does not allow the particle to fall under the well. - In quantum: the attenuation of the perturbation allows the sliding by tunnel effect of the passage of the particle under the well. - In classic: if there is an attenuation of the kinetics at the bottom of the well, then the particle falls under the well.
-
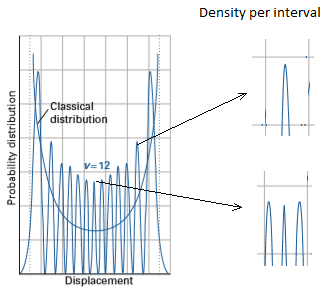
That's precisely why I chose an anharmonic oscillator. To accentuate the slowness of the particle near the turn-around. The number of peaks over an interval. Modified image source: https://www.academia.edu/8950511/Molecular_Quantum_Mechanics_4th_ed_ATKINS-FRIEDMAN
-
I'm still struggling to understand why. The importance that I attach to it, is precisely that the probability distribution is greater at the extremities*, whereas the probability density is greater at the bottom of the well. What is the factor in the equation that acts on a larger presence of the particle with the probability distribution, when the potential energy is higher; since the probability distribution depends on the shape of the potential well? *And above all, is this form of distribution valid for a classical harmonic oscillator? The distribution must be uniform following the shape of the well, because: This is the case for a classical harmonic oscillator. Clearly, is there a probability distribution equation for a a classical oscillator?
-
Yes, of course. I don't know what it's worth, but I see the cosmic inflation part in it too.
-
No, I don't know any. Here's a graph of a decaying continuity under the potential well, but where the particle is never found.