Kartazion

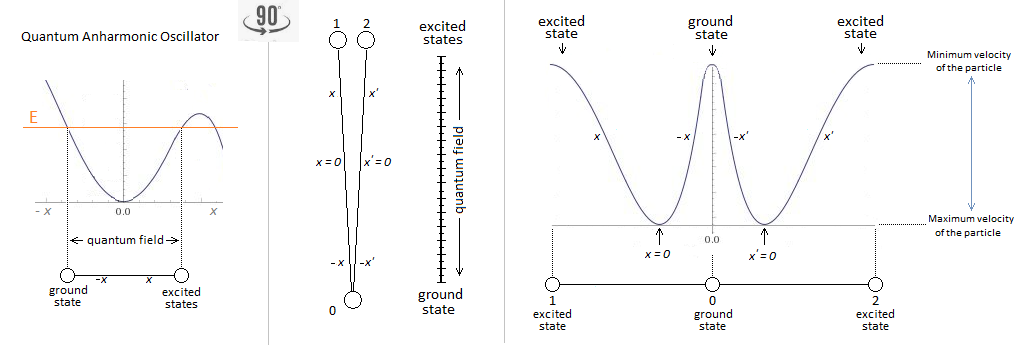
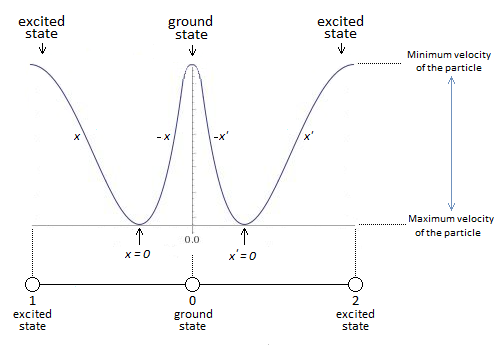
Graphics are mandatory for me. I'm not talking about abstract math. But we are talking about an oscillator. It is precise and tangible. Algorithms and graphs transform well into integrated circuits or into computers and other technological jewels. Clearly there is always a physical support to the key, and gives a concise representation. Just as math tries to explain the creation of our universe. Industrially speaking we do not do math to create imagination. Any formula must be able to represent reality in calories, forces, speed, intensity, ect ... I'm not saying there is no abstract math in real, but the goal is physical design. Is this not the case for quanta?

What I see is the importance of the density at its points *. Namely at the ends of A and B. After that there remains a coherent state, except that for this example it is simply pressed; It is, as I understand it, a real method of application; which we cannot achieve with my classic oscillator, because alternating a particle of mass m to several million cycles per second is not too possible. * The only probability that I see is that of the presence of a density at a given point, or then a specific part of the wave; namely to isolate an alternation either high or low, and deduce that its probability of being up or down is equal. The images help me, as much as a graph describes its equation. But in terms of the formulation I count precisely, and hence my presence here, on geniuses or academics who may one day bring the equation to what I wish to present. What is the difference between a classical and quantum oscillator? It must be a particle of mass m against a quanta of light for example. If I chose the harmonic oscillator, it is for its termination in terms of travel along x. Whether the oscillator is harmonic or anharmonic works on the same principle, only its termination. On the contrary. I would be happy to see someone find a mathematical approach to the problem posed. I work on the rest (details).

My point seems right.

A new method for constructing squeezed states for the isotropic 2D harmonic oscillator We introduce a new method for constructing squeezed states for the 2D isotropic harmonic oscillator. Based on the construction of coherent states in [1], we define a new set of ladder operators for the 2D system as a linear combination of the x and y ladder operators and construct the SU(2) coherent states. The new ladder operators are used for generalizing the squeezing operator to 2D and the SU(2) coherent states play the role of the Fock states in the expansion of the 2D squeezed states. We discuss some properties of the 2D squeezed states.

We can easily deduce the Fock state and the Fock space in the second quantization. In this approach, the quantum many-body states are represented in the Fock state basis, which are constructed by filling up each single-particle state with a certain number of identical particles. ... The Fock space is an algebraic construction used in quantum mechanics to construct the quantum states space of a variable or unknown number of identical particles from a single particle Hilbert space H.

Can the second quantization be read along x for one particle as in the diagram below?

######################### Is Zero-point energy a coherent state of the oscillator? And there is a link between the Second quantization and the Second quantum theory?

Is learning the anharmonic oscillator mandatory to understand quantum mechanics? Or is it simply a substitute calculation method compared to others?

If you want to learn quantum mechanics you have to understand the an·harmonic oscillator. We can say that our universe is then an an·harmonic oscillator. It is the future.

It's still weird as a novice to get there ... So how is it that starting from a simple oscillator I arrive at the foundations of quantum mechanics? I never said it works with a single particle for fun. It is a practicality deduction. Always and with the an·harmonic oscillator I will post something in relativistic physics related to time dilation.

But we can see some correspondence between a wave function and the probability distribution for one particle in quantum mechanics, no? I found that: Definition (one spinless particle in one dimension) Position-space wave functions If the particle's position is measured, its location cannot be determined from the wave function, but is described by a probability distribution. ################################### I would like to know if there is a link between the harmonic oscillator, and the time translation symmetry?

I saw something related to thermodynamics and black holes with the backward in time. New law implies thermodynamic time runs backwards inside black holes

https://arxiv.org/abs/quant-ph/0008036

I deduced from this that matter only appears when we look at it. The rest is only a wave of probability of presence of the particle. The quantum system is suddenly lazy.

There are no particles, there are only fields

Hello. I see that this paper is relevant in the context of the imaginary part of the ground state of the harmonic oscillator in relation to the coupling constant. The power of the method is illustrated by calculating the imaginary parts of the partition function of the anharmonic oscillator in zero spacetime dimensions and of the ground state energy of the anharmonic oscillator for all negative values of the coupling constant g and show that they are in excellent agreement with the exactly known values. How important is this publication, if there is one? Thank you.

You also meant spin 1, right? Or did you specify that the scalar boson of spin 0 is the Higgs boson? I understand that there can be as many bosons as wanted in the same state in the same space, because it does not respect the Pauli exclusion. This means that the QFT gets to explain it better and differently?

This means that the Dirac Sea has as much antielectron as there is room in the negative energy (problematic). Since there were infinitely many negative energy states available, and thanks to the Pauli exclusion principle, we can fill the negative energy space with all possible antielectron states. If an electron appears on the surface (positive energy) then it creates a hole in negative energy which is identified as positron. However for the bosons I do not know how it works with the antimatter.

Theory before the Higgs find. Source: Will the LHC Look into the Fate of the Universe? http://inspirehep.net/record/790889 https://arxiv.org/abs/0807.2601

I only found that of the four forces. Where to find others? Can I define the true vacuum as the graph below if The Higgs vacuum expectation value is 246 Gev? It is certain that if the system were at zero fluctuation of the particle at zero point energy, then we could not exist.

It's 114 different kinds? Or so that means that the coupling constant does not follow a function? Does this mean that the ground state cannot be in the true vacuum? A potential with two false vacua, φ = φ A , φ B , and one true vacuum, φ = φ C Where φA is Higgs' false vacuum. But how to incorporate the true vacuum into the Higgs field?

I found these two explanations: https://en.wikipedia.org/wiki/Yukawa_potential https://en.wikipedia.org/wiki/False_vacuum Back to previous graph:

The coupling constant can be measured with the potential energy well of the harmonic oscillator. In fact, the interaction becomes weaker when the particle converges to its ground state. In other words the levels of the coupling force is proportional to x.