-
Posts
569 -
Joined
-
Last visited
-
Days Won
1
Content Type
Profiles
Forums
Events
Everything posted by Kartazion
-
This makes the link between the strong interaction, the weak interaction, and quantum electrodynamics, right? Do we use the same coupling constant? Is it proportional?
-
I have to understand what a symmetry group is. Here are some links I found. For some, it is difficult to get the paper. - The complete symmetry group of a forced harmonic oscillator - Symmetry groups and conserved quantities for the harmonic oscillator - The symmetry group of the harmonic oscillator and its reduction - U3 symmetry and clustering in the harmonic oscillator shell model Density is determined only if the particles are correlated / observed. Otherwise you have to stick to the probability of the wave function, only. No? It's why Albert Einstein said: "I like to think the Moon is there even if I am not looking at it."
-
I deduce that our universe works with a single moving particle. John wheeler had already had this idea with the electron. https://en.wikipedia.org/wiki/One-electron_universe What do you think about?
-
So the connection between quantum decoherence and coherent states it would be with Schrödinger's equation...
-
I don't know if it has to do with quantum decoherence, but I also saw this link: https://en.wikipedia.org/wiki/Coherent_states In physics, specifically in quantum mechanics, a coherent state is the specific quantum state of the quantum harmonic oscillator, often described as a state which has dynamics most closely resembling the oscillatory behavior of a classical harmonic oscillator.
-
I expected the wave function to disappear, to an excited atomic state. But apparently it's just a matter of interference.
-
-
I understand for the moment the Minkowski diagram and its metric starting from the principle where the tensor is composed of its four dimensions. Then follows the Lorentz invariance in relation to its transformations. Next in its basic explanation, and more new to me, is renormalization, which determines a quantified finiteness at an infinite phase; indeed this is all the more true for a loop. The Wick rotation remains vague for me, even if I understand its loop diagram cut in the y axis to insert a junction of the infinite loop. However I still struggle to get used with the Lagrangian. I will now take a winding path to better understand. During quantum decoherence, is the ground state of a particle considered as a correlated state? In other words, does the correlated matter come exclusively from the excited state of the atoms, or so also requires the ground state? I am not saying that the system does not need the ground state, it is just during the wave function collapse or for the density matrix approach.
-
It's a little bit hard to find something about the Wicks rotation in gravity. I saw a report with the path integral formulation. It's very technical. However, with the Wicks rotation here, I found that : Wick rotation connects statistical mechanics to quantum mechanics by replacing inverse temperature 1/(kBT) with imaginary time it/ℏ. Consider a large collection of harmonic oscillators at temperature T. The relative probability of finding any given oscillator with energy E is ... Now consider a single quantum harmonic oscillator in a superposition of basis states, evolving for a time t under a Hamiltonian H. ... The divergences of gravity? The different operating techniques?
-
Let’s say that if you manage to join relativistic gravity with quantum mechanics then it’s won. So yes it's wobbly but very ingenious for the LQG.
-
We have the Loop quantum gravity https://en.wikipedia.org/wiki/Loop_quantum_gravity or https://en.wikipedia.org/wiki/Quantum_gravity But I found that A_quantum_oscillator_that_could_explain_gravity (I don't know what it's Worth)
-
The radiation ? Good after I do not know if I had presented it correctly, but an expert told me here and with the oscillator "you need a new model for EM radiation, because that's not how it works." Indeed I found that: http://farside.ph.utexas.edu/teaching/qmech/Quantum/node120.html So I'm going to reverse my question. What cannot we calculate with the harmonic oscillator in quantum mechanics? Thank you.
-
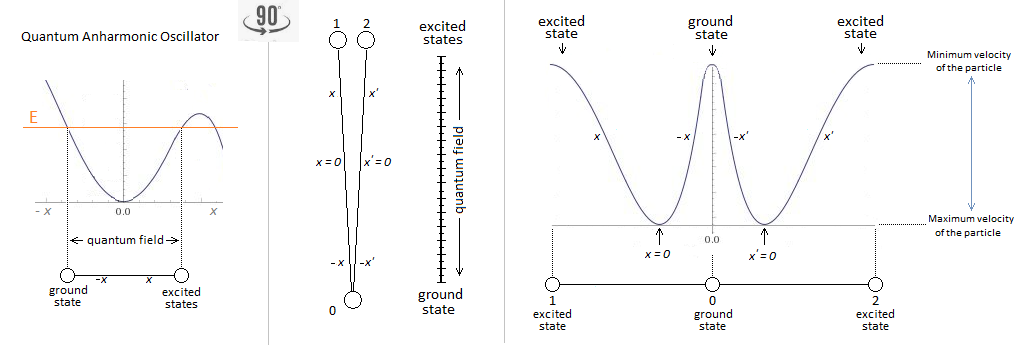
Good morning I see that the anharmonic oscillator is rare in quantum physics. But I know that anhanamorcity interprets internuclear distance (Morse). Is there another anharmonic role in quantum physics / mechanics?
-
It is thanks to your help. Ok Yes it's always on the move. Of course, in classical physics we can always determine the two values simultaneously. ################### Otherwise I would have a weird calculation to do. I want to know if it is possible to have an infinitesimal interval ℏ and express the velocity as: $$\frac{\hslash x}{\hslash t}$$ I don't think so, but I wish to be able to calculate the oscillator in an unusual direction. Example:
-
I have just found here some good equations concerning the uncertainty principle. Which brings me to two questions. The first concerns the equation of the minimum energy of the oscillator. In normal times we cannot simultaneously to know the position and the momentum of the subatomic particles. The question is: the uncertainty principle also applies on the quantum harmonic oscillator with \Delta x and \Delta p ? Is this what makes the difference with the classical harmonic oscillator? My second question is: why do we use the Planck constant so often in the equations of the quantum harmonic oscillator to express the principle of uncertainty?
-
Yes thanks. I also saw it with Schrödinger equation. But I look forward to see with the uncertainty principle.
-
In what other area of quantum mechanics are we using precisely the harmonic oscillator? There is already : 1 - In solids with the vibration of atoms, where if we move the atoms slightly away from its equilibrium position, a restoring force will try to put the molecule back in the equilibrium position. 2 - For coherent states, among others used to describe the states of light of lasers. and what other domain? Thank you
-

The solution of the Cosmological constant problem ?
Kartazion replied to stephaneww's topic in Speculations
I don't really know. I think you should continue. -

The solution of the Cosmological constant problem ?
Kartazion replied to stephaneww's topic in Speculations
The QED is a physical theory aimed at reconciling electromagnetism with quantum mechanics using a Lagrangian relativistic formalism. According to this theory, electrical charges interact by exchanging photons. -
Ok. Otherwise I found that: Connection between Coulomb and harmonic oscillator potentials in relativistic quantum mechanics
-
####################### I saw on a thread a link, here, which shows this potential energy between a1 and a2. From arXiv here, I read "The Coulomb system of identical particles obeys equations that have the structure of the cosmological equations of the general theory of relativity." This is the part of the general theory of relativity that made me think, because my question is: Can we rally the Coulomb-Newton correspondence relation with the anharmonic oscillator? If yes, is there a direct relationship with the potential energy from $$ Ep(x)=\frac{1}{2}Kx^2 $$ ?
-

Quantum Chromodynamics with a Single Particle in Motion
Kartazion replied to Kartazion's topic in Speculations
Yes i will take care of the quantum field theory. Thanks for the support. -

Quantum Chromodynamics with a Single Particle in Motion
Kartazion replied to Kartazion's topic in Speculations
I really have a job. -

Quantum Chromodynamics with a Single Particle in Motion
Kartazion replied to Kartazion's topic in Speculations
Yes thanks. It's a story of fermion and boson (half-integer spin with antisymmetric wavefunctions (-), and particles of integer spin with symmetric wavefunctions (+)) Let the quarks on one side and the gluons on the other. The use of Pauli exclusion is only applied with fermions (antisymmetric). So now I understand better the writing of the principle. What do you advise me next to understand better the QCD? -

Quantum Chromodynamics with a Single Particle in Motion
Kartazion replied to Kartazion's topic in Speculations
I only know CPT symmetry or SU(3) symmetry for QCD. Maybe that's what you're talking about, because I did not find anything on the symmetric and anti symmetric commutations. I also saw this link https://en.wikipedia.org/wiki/Anti-symmetric_operator but I do not know what it's Worth. Thanks