Kartazion

I am talking about the speed of the particle given by the impulse.

Yes. This is because it derives from: $${\displaystyle \Delta x\Delta v\ \ {\ge } \ {\frac{\hbar}{2m}}}$$ I meant the speed of acceleration of the particle during ejection. How to know its speed?

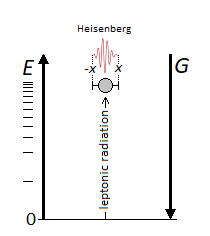
I had forgotten that g was constant. So it doesn't work with variable acceleration. I now wish to include Heisenberg's Uncertainty Principle in the formula. Can we write the following form? $${\displaystyle \Delta x\Delta p\ = \sqrt{2m^2\ g\ (H-h)} \ \ {\ge } \ {\frac{\hbar}{2}}}$$ Since the projection of the particle is radiative, only one interval value of x is needed. Let x = 1 and constant. The amount of movement seems fixed. But by the principle of uncertainty, it is said that it is constraining to keep a constant value x for a macroscopic object.

Like this? $$v=\sqrt{2gh}$$ All that's missing is acceleration to finish. How is acceleration written with the same form of formula?

This model does not include colision. I now wish to associate the value v of the speed into: $$\sqrt{2m^2\ g\ (H-h)}$$ Thanks.

Hello. At each departure the particle is subjected to an impulse to eject it vertically. The linear momentum decreases in relation to as it increases in height and the gravitational force that causes it to fall. How do you think we could write the forumle of momentum associated with gravitational force and on impulse? The particle is of identical mass.

I don't see where the neutrinos are.

@Holmes What do you think about that: Nondeterministic Turing machine - Wikipedia

As long as you consider an algorithm to be a computation. Nondeterministic algorithm - Wikipedia

Schematic example of Comparison of deterministic and Non-deterministic computation.

Windows key + X and choose PowerShell admin in the list.

@Heis3nberg It's not the simplest subject. I do not see any related question apart from the historical facts. To verify this hypothesis one avenue envisaged is to compare the flux of neutrinos detected between day and night. Indeed, at night, solar neutrinos, to be detected, must cross the whole of the Earth, and should therefore be able to oscillate by interaction with matter, therefore at a rate different from the oscillation in vacuum, which should cause a flux detected different from that detected during the day. In addition, such an experiment would allow us to better understand the periods of these oscillations, which would improve our understanding of the phenomenon. But currently, the detectors are not sensitive enough to allow this measurement. I do not understand everything to get this equation, but I found this form of expression where the probability equation becomes: P=|〈νe|ν(t)〉|2≈|〈νe|ν2m(t)〉|2=|〈νe|ν2〉|2≈sin2θ≈13 A deviation from the value of the sin²θ probability is an indication of the presence of oscillations.

Hello. Before making a hypothesis, I would like to know if anyone are already familiar with a physical and/or mathematical approach to a junction between Coherent States and the Second Quantization? Thanks. References: [1] [2]

The sea currents would have gnaw the part sunken. The sysmic movements would have split the rock.

Looks like the highest point of a volcano crater.

The advantage of this forum is that we can do science. The toy, for example, can be made of plastic or metal. What about your ball? Or what is the difference between your ball, and a quantum particle?

Can you define what you call Tesla ball? I recall that the tesla is the unit T derived from electromagnetic induction.

Ok. And what does this discovery say? What do you understand in it? Thank you

The only importance that has Higgs, is to be able to explain the mass of the particles.

I think it might be difficult then. See impossible. The problem is that you have to have done many years of learning in relativistic or quantum physics to understand how our nature is already made. For example we already know the speed of light or we can predict the movement of celestial objects. However, the techniques used can be explained without math, even if we must have the math to be able to constitute such a measuring device. I'm sorry, but what you're saying doesn't make sense.

Hello. For my part, I also have my idea of how the universe works. All without doing maths. Yet I am able to understand quantum mechanisms enough well with their operating principles. The question is: What is the linkage mechanism between GR and QM, and with your God particle? Please use the appropriate technical terms. Thank you.

The hiberfil.sys file is used by Windows to store the current state of your computer (memory contents, open applications and documents, etc.) during hibernation. If you are not using hibernation, you can turn it off so that you can delete the hiberfil.sys file and reclaim all the space it was using. Note that the classic standby will then still be usable. To deactivate and delete the file in command prompt (admin) type: powercfg.exe /hibernate off To re-activate hibernation type: powercfg.exe /hibernate on

I'm really bad at math, but the trigonometric rotation? Here is what I found. To check. Strictly positive reals have an argument that is multiple of 2π, strictly negative reals have an odd multiple of π as argument. Pure non-zero imaginaries have an argument congruent to π/2 or –π/2 modulo 2π, depending on the sign of their imaginary part. The particular values, which are the intersections of the trigonometric circle with the real and imaginary axes, are: $${\displaystyle \operatorname {e} ^{\mathrm {i} 0}=\operatorname {e} ^{0}=1}\\ {\displaystyle \operatorname {e} ^{\mathrm {i} \pi }=\cos \pi +\mathrm {i} \sin \pi =-1}\\ {\displaystyle \operatorname {e} ^{\mathrm {i} \pi /2}=\cos(\pi /2)+\mathrm {i} \sin(\pi /2)=\mathrm {i} }\\ {\displaystyle \operatorname {e} ^{\mathrm {i} (-\pi /2)}=\cos(-\pi /2)+\mathrm {i} \sin(-\pi /2)=-\mathrm {i} }\\ {\displaystyle \operatorname {e} ^{\mathrm {-} i(\pi /2)}=\cos(\pi /2)-\mathrm {i} \sin(\pi /2)=-\mathrm {i} }\\$$

The use of seeds is very controlled. Unfortunately for agricultural producer in Europe, the reuse of seeds is prohibited. You must to repurchase the seeds. Seed laws that criminalise farmers: resistance and fightback Genetic?

This is the role of the compiler. Early computer software was written in assembly language corresponding to processor instructions, and early compilers were written directly in assembly language. In general, the source language is "higher level" than the target language, that is, it presents a high-level of abstraction. An interpreted language as JavaScript, Python, Perl, etc, is a programming language which are generally interpreted, without compiling a program but instead read and executed by some other program. AFAIN not really. The flags is an additional processor informations. It allows you to set and know the state of the processor at any time thanks to the different bits that compose it. This register thus makes it possible to have at any time the state resulting from an instruction having been executed by the processor. FLAGS register - Wikipedia