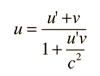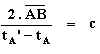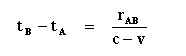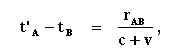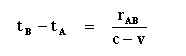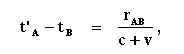-
Posts
67 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by vanholten
-

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
I am afraid one frame is enough to undo the relativity of all others. -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
But if these were the first two objects in the universe, they were not in motion relative to something else. By the absence of any reference they were at an absolute distance.Their geometrical relation in relativity still is a definite line segment. I just don’t see the theoretical need for stating that both endpoints of a segment are at rest with respect to each other. And what do you think of the following? If two objects are in uniform motion, a point of rest exists from which these objects move away in opposite direction at half their relative velocity. -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
Too busy crackpotting everyone with and deviant view you apparently forgot to prove that my calculations resulting in the zero velocity are plain wrong. I was hoping for that actually. Because if my childish calculations are right there is no fundament for special relativity whatsoever. Perhaps reading that wordy and formal 100 years old text with a bit more attention will help you understand why. -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
Apparently you are unable to comprehend the simple concept of relative motion. You seem to have missed that the relations between the clock and their observers essential to define motion can't be relative, since nobody can be in relative rest compared to a stationary object. Rest defines a definite or absolute relation. SR totally relies on that definite relationship. Imagine empty space. What is to be defined first, rest or motion, or relative motion? How many positions do you need to define rest? And how many positions do you need to create motion? Once you know, you might even have the answer to how many positions you need to experience relative motion. -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
It relies on the all seeing eye. To establish simultaneity you need at least two events, a rhombus and two observers at opposite edges. I already showed that you can easily derive the Lorentz-transformation using the pythagorean theorem. -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
Have a nice evening. And many thanks for your kind offer. -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
Thanks for that I have no trouble understanding it. However I was explaining that Einsteins equations inevitably result in zero velocity. It takes to many words. Explaining my findings in Dutch is already difficult , and doing so in English is even more complicated. So let me once again try to explain what I mean, again based on Einstein's equations. The distance the light beam travels can be expressed as rAB + v . ( tB - tA ) or c . (tB - tA) + v . (tB - tA) Because all clocks on the moving rod and in the stationary system are synchronized, what Einstein assumed is: tB - tA = { rAB + v . ( tB - tA )} / c ............... leads to the original "tB - tA = rAB / (c - v)" or tB - tA = { c . (tB - tA) + v . (tB - tA)} / c tB - tA is replaced by x then x = (c x + v x)/ c take for example c = 1 then x = ( x + v x) thus v = 0 WolframAlpha confirms: "Solutions: v = o, c ≠ 0 x = 0, c ≠ 0 v = 0" Einsteins "tB - tA = rAB / (c - v)" results in zero velocity. -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
To illustrate the effect of length contraction Einstein sketched an experiment. Rod AB in motion is equipped with clocks and observers at each end. The whole thing is observed from a stationary system with synchrone clocks all over the place. The clocks on both ends of the moving rod AB are synchronized with the clocks of the stationary non co-moving observers. Ok this is what I assumed: The two equations are meant for the stationary observers seeing the rod AB in motion. Because those observers will have to deal with the velocity of the rod, as formulated in both equations. And they rely on the timespan tB-tA displayed by their clocks being part of the first equation. Einstein says that the length of rod AB in motion is measured as being different from the length of rod AB when it is measured as a stationary object. It seems he relies on length contraction, adapted from Lorentz' explanation of the absence of phase shift during the MM experiment. (I think that is strange because the second postulate did us forget about the ether.) Anyhow, Einstein says : “rAB denotes the length of the moving rod—measured in the stationary system. “ But what does he mean by that? I think there are two explanations possible. Option 1: rAB is measured in the stationary system; the stationary rod is measured to have the length AB. In that case the stationary observers see the light ray bridge the distance AB according to their clocks in tB-tA seconds. According to Einstein's definition of simultaneity: 2AB/(t’A-tA) = c and tB-tA = t’A-tB they measure the light to propagate at c so their observation results in rAB/c = tB-tA ( my assumption) Option 2: rAB is measured from the stationary system while the rod AB is in motion. The speed of light is measured to be c as always for all observers. The stationary clocks still display the timespan tB-tA in which the light at c bridges AB. Again this results in rAB/c = tB-tA (my assumption) Both explanation have the same result. For the stationary observations the velocity v in both equations is a meaningless parameter. However Einstein’s experiment suggests that the observers on the rod encounter a different timespan for the light to travel AB. This means that for those observers the timespan should result in rAB/c ≠ tB-tA because their clocks are synchronized with the clocks in the stationary system; the system being not Rod AB. To make the confusion complete: Thanks to the equations the observers that are stationary with respect to rod AB are no longer subjected to the definition of simultaneity; 2AB/(t’A-tA) = c Instead they have to bring the relative motion of the clocks in the non co-moving system into account. But the equations don't deliver the required parameters to do so. Because by the lack of simultaneity these observers on the rod can't produce a sensible value for velocity v. In other words: The clocks at both ends of the rod are asynchrone so the observers can't define the relative speed of the other system required to pinpoint v in the equation. Thus also for them v in the equations is pointless. And if they would adjust their clocks to achieve rAB/c = tB-tA, they would have only switched sides and end up with the same observations as made by the observers in the stationary system; velocity is irrelevant. The intriguing thing is that the second postulate underlines the irrelevance of velocity of the light source during the measurement of the speed of the light emitted by that source. I never assumed the speed of light is infinite. -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
I already tried to explain it in a previous topic. 'What if Einstein's definition of simultaneity is incorrect" The mathematical passage is in here: hermes.ffn.ub.es-luisnavarro-nuevo_maletin-Einstein_1905_relativity.pdf.webloc 1. Kinematical part § 1Definition of Simultaneity and §2 On the Relativity of Length and Time. tB - tA = rAB / (c - v ) and t’A - tB = rAB / (c+v) These equations are based on the length contraction of rod AB. To retrieve the first equation I followed the "einsteingenootschap.nl" (a Dutch site dedicated to Einstein) 1- The distance the light beam travels can be expressed as: rAB + v . ( tB - tA ) Because all clocks on the moving rod and in the stationary system are synchronized, what Einstein assumed is: tB - tA = { rAB + v . ( tB - tA )} / c c . ( tB - tA ) = rAB + v . ( tB - tA ) c . ( tB - tA ) - v . ( tB - tA ) = rAB ( c - v ) . ( tB - tA ) = rAB And there it is: tB - tA = rAB / (c - v) So far so good and in line with the einsteingenootschap. But next I assume that the following is allowed: tB - tA = { rAB + v . ( tB - tA )} / c rAB / c = { rAB + v . ( rAB / c )} / c I replace Rod AB by length L L / c = { L + v ( L /c )} /c L = L + v ( L /c ) L . v / c = 0 L = 0 , c ≠ 0 v = 0 , c ≠ 0 L = rAB ≠ 0 thus v = 0 Both fundamental equations of Special Relativity eliminate motion? -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
Sorry You wrote that Lorentz and Fitzgerald explained the absence of interference due to length contraction. Then they must have supported the idea of the ether I presume. So why did Einstein at one hand adapt the Lorentz/Fitzgerald contraction as the fundament of simultaneity according to tB - tA = rAB / (c - v ) and t’A - tB = rAB / (c+v) and at the other made the ether superfluous with his second postulate? -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
The idea that there is not even an actual reflection is the whole point. It is supposed to be remittance of energy in the shape of a new photon; a fresh emission creating a fresh wave propagating at c. If that is going on the mirrors act like stationary light sources with respect to the telescope. From a relativistic perspective there is only a single stationary frame of reference, which as such can't confirm the second postulate. The thing you might expect caused by the rotation of the interferometer is the Sagnac effect. But that effect is predicted based on classic physics and adapted by relativity, so neither the Sagnac effect can be a confirmation of SR. I agree it makes you wonder why the remittance of light by electrons is forced in the reflective angle. It needs an explanation. Probably it is imposed by the collaboration of surrounding electrons in the reflective surface? -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
Sure it wasn’t discovered but it was acting anyhow. So what is your point? Earth wasn’t flat before it was discovered to be sphere. The fact that at the current state of science according to you is impossible to describe the speed of individual photons doesn’t imply it’s meaningless. It might even be essential to get a grip on the behaviour of light. -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
https://en.wikipedia.org/wiki/Reflection_(physics) "mechanism" -"In the case of dielectrics such as glass, the electric field of the light acts on the electrons in the material, and the moving electrons generate fields and become new radiators. The refracted light in the glass is the combination of the forward radiation of the electrons and the incident light. The reflected light is the combination of the backward radiation of all of the electrons."- This says the mirrors become radiators that emit light at c independent of their relative motion as usual. The telescope in the MM experiment is the stationary observer of the mirrors so it should measure the light within the instrument to propagate at c. It is not even a relativistic observation. That is why I don't t see why this experiment confirms the second postulate. It only comments the ether or on the absence of it. -

Michelson Morley experiment is no confirmation of Special Relativity
vanholten replied to vanholten's topic in Speculations
My point is that the MM experiment is frequently brought forward as confirmation of the second postulate. If your assumption would be correct it would undermine the theory of SR and its underlying calculations all by itself. -
Hello. Excuse me, but I do question the relevance of the Michelson-Morley experiment regarding Special Relativity. At the time the MM interferometer didn’t show any phase shift at the receiver within the instrument. The outcome of the MM experiment suggests that the velocity of Earth relative to the Sun being the light source, had no effect on the measurement of the propagation velocity of sunlight in neither directions. This absence of phase shift is considered to be a confirmation of the second postulate of Special Relativity: “2. Second postulate (invariance of c) As measured in any inertial frame of reference, light is always propagated in empty space with a definite velocity c that is independent of the state of motion of the emitting body. Or: the speed of light in free space has the same value c in all inertial frames of reference.” But is the absence of phase shift indeed a solid confirmation of second postulate postulate? Not quite I think. To measure the propagation velocity of light, you should measure the velocity of one and the same photon. (@swanson) In the decennia after the MM experiment and SR, Quantum mechanics evolved mead thanks to Einstein explanation of photo-electric effects. The interferometer makes use of mirrors. However when a photon strikes a mirror and it would be absorbed by an electron, that electron will be excited, gaining energy and momentum. Later, it will drop back to the previous state, emitting a photon. When indeed the electrons in the mirrors of the interferometer act like light sources, they will emit other photons than those being intercepted and absorbed from the sunlight. If that is true the MM experiment compares the velocity of different photons coming from different light sources. Of course photons emitted by the MM mirrors would have propagated at the velocity of light but independently from the photons emitted by the Sun. The fact that no phase shift occurred seems to be exactly in line with quantum mechanical effects and as such is no confirmation of Special Relativity at all. Perhaps to do a proper test to confirm the irrelevance of motion of the light source, one should make use of the refraction index of light, because that alters when the speed of light deviates.
-

What if Einsteins Definition of Simultaneity is incorrect?
vanholten replied to vanholten's topic in Classical Physics
Let me emphasize that no chain of reasons ending in Einstein definition of simultaneity can retrospectively justify the inevitable v = zero outcome of the equations, from which all other calculations in § 3 and further are derived. tB - tA = rAB /(c - v ) and t’A - tB = rAB / (c + v) and thus v = 0 The for special relativity devastating prove of the twin equations resulting in zero velocity, also handover the clue on how to interpreted the second postulate. Evaluating simultaneity doesn't make this go away, but if you like I will give it a try. Do you really think the solution to this problem lies in infinitesimally slow transport of clocks? You realize that infinitesimally slow transport results in infinitely long transport time. Meanwhile let me continue with a couple of straight forward calculations that obey Einstein's paper definition of simultaneity and do allow velocity to be a meaningful factor. From "§ 1. Definition of Simultaneity" “In agreement with experience we further assume the quantity 2AB / (t’A - tA) = c to be a universal constant—the velocity of light in empty space.” All distances concerning the motion of the rod AB are measured within the time interval t’A - t A. The equation shows that the length of rod AB is accounted for twice in relation to the universal constant - the velocity of c in empty space. And in accordance with Einsteins definition the two clocks synchronize if: t B − t A = t ′A − t B The completed time interval concerning rAB in motion is tB - tA + t’A - tB During the first timespan tB - tA , rod AB travels the distance Dr = v . ( tB - tA ) To reach B the photon emitted at A needs to travel the distance Dp. At this point we meet the starting calculations of the twin equations in the previous post: rAB + v . ( tB - tA ) The distance the photon travels within a stationary rod AB is c . ( tB - tA ) The forward distance traveled by the photon is Dpf = c . ( tB - tA ) + v . ( tB - tA ) Dpf= ( c + v ) ( tB - tA ) on the way back the distance is Dpb = (c - v) (t’A - tB) The total distance traveled by the photon is D = ( c + v ) ( tB - tA ) + (c - v) (t’A - tB) ( c + v ) (AB/c ) + (c - v) ( AB/c) 2AB and matches “In agreement with experience we further assume the quantity 2AB / (t’A - tA) = c to be a universal constant—the velocity of light in empty space.” Which for all observers has to be true according to the second postulate. These calculations do not violate “t B − t A = t ′A − t B” and support what Einstein wrote:- "while observers in the stationary system would declare the clocks to be synchronous.” So far so good. Now let’s take a look at the observers moving with the moving rod AB. In their perception the velocity of the rod AB is v = 0. The distance traveled by the photon forward equals the distance backwards. D = ( c + 0 ) ( tB - tA ) + (c - 0) (t’A - tB) matching 2AB / (t’A - tA) = c Which for all observers has to be true according to the second postulate. Apparently the calculations apply to either the stationary system and to the system in motion, and match the definitions of simultaneity. So it remains unclear why Einstein wrote: “Observers moving with the moving rod would thus find that the two clocks were not synchronous”. Next: "The second postulate: 2. Any ray of light moves in the “stationary” system of co-ordinates with the determined velocity c, whether the ray be emitted by a stationary or by a moving body." This postulate is difficult to grasp because it says that any observer in motion or stationary compared to a light source measures the light to travel at c relative to himself. Against logic it implies that two observers in relative motion, each measure the light beams from one and the same light source to travel at c relative to themselves. But what if we interpreter the postulate as follows, then what happens? In a system of coordinates any ray of light is measured to be emitted at the definite velocity c regardless of the relative motion of the light source it originates from. It makes perfect sense and remains a valid rejection of the aether theory. But in this interpretation it can't be taken for granted that the velocity of light is measured to be a universal constant, so that must be fixed. To do so we should take another look at rod AB and the calculus of small quantities you mentioned. The velocity of the rod rAB relates to the timespan t’A - tA . This implies that the own length of rAB limits the extent the rod travels during that same time span. Because the motion of rAB is one directional and v < c the distance D within t’A - tA never exceeds 2x the length of rod rAB per definition. "2AB / (t’A - tA) = c" and D= 2ABv/c If AB is chosen to be infinitesimally short, D also approaches zero. Within the accompanying time span the light source is ~ stationary to all observers regardless of their own relative motion. It looks like Einstein indeed chose rAB represented by x' to be infinitesimally small. § 3: Perhaps a more to the point approximation of the narrowest window of opportunity in which velocity can manifest is the emission event of a photon. That emission event is compliant with the average wavelength of light ~ 10-7 m. ( c= λ . f ) “In agreement with experience we further assume the quantity 2AB / (t’A - tA) = c to be a universal constant—the velocity of light in empty space.” It appears to me that the quantity 2AB / (t’A - tA) = c inevitably has to refer to the reasonable assumption that lightwaves are quantities of simultaneity and thus to quantum mechanics and the Planck Constant. At an astronomical scale it is fair to say c + v approximates c - v thus v approximates 0 or even v = 0. The outcome v = 0 brings us back to the twin equations mentioned in the header of this post. From those equations Einstein derived length contraction and time dilation. Length contraction L = L0 √ (1-(v/c)²) or L = L 0/ γ Time dilation Δ t’ = Δ t/ √ (1-(v/c)²) or Δ t’ = Δ t . γ L . Δ t’ = L 0 . Δ t (L 0/ γ) . Δ t . γ = L 0 . Δ t (1/ γ ) . γ = 1 Length contraction shortens the rod and according to D= 2ABv/c as such it travels a shorter distance. Meanwhile due to time dilation it takes more time to bridge that shorter distance. Expressed in m/s the velocity entered in the equations remains unchanged and since the velocity of light is a constant, the relative distance and the length of the rod measured by clocks remain unchanged. At their best TD and LC refer to frequency and wavelength in relation to constant velocity, but nevertheless are doomed to cancel each other out when attempting to produce spacetime curvature. Now let's take a look at both postulates. "1. The laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems of co-ordinates in uniform translatory motion. 2. Any ray of light moves in the “stationary” system of co-ordinates with the determined velocity c, whether the ray be emitted by a stationary or by a moving body." My summary: Any light emitted propagates a the definite velocity c away from the light source regardless of the relative motion of the light-source. For the proper measurement of the velocity of a photon the light source compares to be stationary to any inertial frame of reference. In my opinion the second postulate is no complement but should rather be an exception to the first postulate. In short: Galilean Relativity does not apply to the measurement of the propagation velocity of light. It is about the uncertain relation between measurement, location and impulse. I gather this intriguing issue is finally solved. -

What if Einsteins Definition of Simultaneity is incorrect?
vanholten replied to vanholten's topic in Classical Physics
This is an attempt to demystify some issues concerning Special Relativity. The definition of simultaneity, part two. The Rod AB. "§ 2. On the Relativity of Lengths and Times:"- “Taking into consideration the principle of the constancy of the velocity of light we find that tB - tA = rAB / (c - v ) t’A - tB = rAB / (c+v) where rAB denotes the length of the moving rod—measured in the stationary system. Observers moving with the moving rod would thus find that the two clocks were not synchronous, while observers in the stationary system would declare the clocks to be synchronous.” The diagram leaves no doubt that observers moving with the rod AB read out synchronous clocks, so why Einstein's remark concerning these formulas? A calculation based on v = 0,5 c and the rod rAB having a length of 1 c . sec makes clear something very strange is happening. tB - tA = (1c . sec) / 0,5 c results in tB - tA = 2 sec. t’A - tB = (1c . sec) / 1,5 c results in t’A - tB = 0,666 sec. Although working in opposite direction, the formulas do not compensate for each other but have a very complex relation. Apparently something strange happened to the length of the rod. “The length to be discovered by the operation (b) we will call “the length of the (moving) rod in the stationary system.” This we shall determine on the basis of our two principles, and we shall find that it differs from l.” Differs how? Length contraction or time dilation, both or neither? I claim the formulas above are based on a biased perception that is actually a mistake. The distance the light beam travels can be expressed as: rAB + v . ( tB - tA ) Because all clocks on the moving rod and in the stationary system are synchronized, what Einstein assumed is: tB - tA = { rAB + v . ( tB - tA )} / c c . ( tB - tA ) = rAB + v . ( tB - tA ) c . ( tB - tA ) - v . ( tB - tA ) = rAB ( c - v ) . ( tB - tA ) = rAB tB - tA = rAB / (c - v) Mathematical it’s ok, however the following is allowed: tB - tA = { rAB + v . ( tB - tA )} / c rAB / c = { rAB + v . ( rAB / c )} / c Rod AB is replaced by L L / c = { L + v ( L /c )} /c L = L + v ( L /c ) L . v / c = 0 L = 0 , c ≠ 0 v = 0 , c ≠ 0 L = rAB ≠ 0 thus v = 0 This proves the formula only applies to the situation in which v = zero and therefore is pointless regarding the concept of relative motion. -
Giving each clock a speed of 0.8c relative to a point halfway AB you simulate a relative velocity of 1.6c between clock 1 and clock 2. Doing so you created the conditions to apply the formula of relativistic velocity transformation. In this formula relativistic simultaneity is integrated, so your workaround is no clarification of time dilation itself. In my example the relative velocities did not necessarily overreach c. The relativistic velocity transformation results in u’= 0 thus u= v and the formula doesn't shed light on the frequency issue. Sorry, but what you cross marked is not the frequency rate of the clock. BTW I feel my comment is obscuring the point made by the OP, so I bail out. Pasted Graphic_edited-1.tif
-

What if Einsteins Definition of Simultaneity is incorrect?
vanholten replied to vanholten's topic in Classical Physics
Indeed, tell me. I read all kinds of alogical explanations by people that pretend to understand Special Relativity. -

What if Einsteins Definition of Simultaneity is incorrect?
vanholten replied to vanholten's topic in Classical Physics
No, I didn't. I only got really interested in the subject about a year ago. Thanks I will look into it. -

What if Einsteins Definition of Simultaneity is incorrect?
vanholten replied to vanholten's topic in Classical Physics
Actually it does. If Janus would be right what is the point of simultaneity? Einstein is saying a lot more than that the speed of light is the same in both directions. This is what Einstein wrote on page 2. the third alinea of Definition of Simultaneity: "We have to take into account that all our judgments in which time plays a part are always judgments of simultaneous events." This is true because simultaneity is an essential expression of the order of nature. Take the second law of Kepler for instance: -A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. Isn't it amazingly wonderful? You can't change the simultaneity of natural events by synchronizing manmade clocks to your own liking, you have to look further than that. -

What if Einsteins Definition of Simultaneity is incorrect?
vanholten replied to vanholten's topic in Classical Physics
According to Einstein: "We have so far defined only an “A time” and a “B time.” We have not defined a common “time” for A and B, for the latter cannot be defined at all unless we establish by definition that the “time” required by light to travel from A to B equals the “time” it requires to travel from B to A. Let a ray of light start at the “A time” tA from A towards B, let it at the “B time” tB be reflected at B in the direction of A, and arrive again at A at the “A time t′A.” In accordance with definition the two clocks synchronize if t B − t A = t ′A − t B ." The definition of simultaneity implies that if C takes part in the simultaneity of A end B the following should be true for clocks A, B and C: t B − t A = t ′A − t B and t C− t A = t ′A − t C and t B− t C = t ′C − t B "§ 2. On the Relativity of Lengths and Times" (page 4:) "velocity = light path/time interval" Simultaneity between the stationary clocks depends on the velocity of light and requires equal time intervals. Equal time intervals require equal distances. -
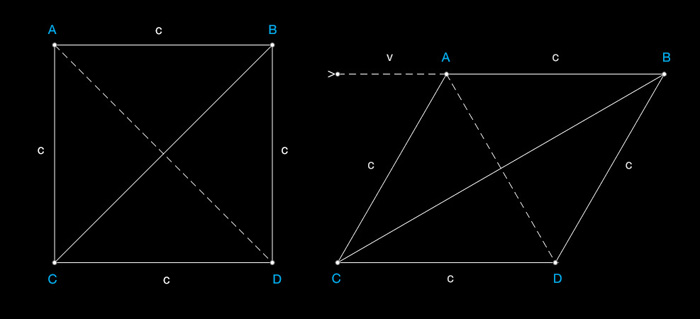
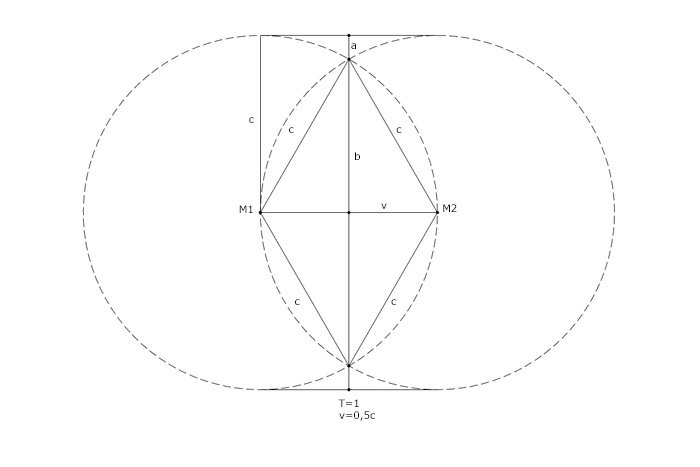
Hello, is it even possible that Einsteins definition of simultaneity is incorrect? Based on his paper I wrote down a number of reasons why I think the definition is plain wrong. (The paper I quoted from you can find clicking the link below). I. KINEMATICAL PART § 1. Definition of Simultaneity (p.3) -"We arrive at a much more practical determination along the following line of thought. If at the point A of space there is a clock, an observer at A can determine the time values of events in the immediate proximity of A by finding the positions of the hands which are simultaneous with these events. If there is at the point B of space another clock in all respects resembling the one at A, it is possible for an observer at B to determine the time values of events in the immediate neigh- bourhood of B. But it is not possible without further assumption to compare, in respect of time, an event at A with an event at B. We have so far defined only an “A time” and a “B time.” We have not defined a common “time” for A and B, for the latter cannot be defined at all unless we establish by definition that the “time” required by light to travel from A to B equals the “time” it requires to travel from B to A. Let a ray of light start at the “A time” tA from A towards B, let it at the “B time” tB be reflected at B in the direction of A, and arrive again at A at the “A time t′A.” In accordance with definition the two clocks synchronize if t B − t A = t ′A − t B . We assume that this definition of synchronism is free from contradictions, and possible for any number of points; and that the following relations are universally valid: 1. If the clock at B synchronizes with the clock at A, the clock at A synchronizes with the clock at B. 2. If the clock at A synchronizes with the clock at B and also with the clock at C, the clocks at B and C also synchronize with each other. Thus with the help of certain imaginary physical experiments we have settled what is to be understood by synchronous stationary clocks located at different places, and have evidently obtained a definition of “simultaneous,” or “synchronous,” and of “time.” The “time” of an event is that which is given simultaneously with the event by a stationary clock located at the place of the event, this clock being synchronous, and indeed synchronous for all time determinations, with a specified stationary clock.” Einsteins assumption that his definition is possible for any number of points and that the relations are universally valid, is untenable and so is his conclusion, because: - If the clock at A synchronizes with the clock at B and also with a third clock at C, these clocks only synchronize under the condition that the distances in between all three clocks are equal. Or: It requires the clocks to be placed on the vertexes of an equilateral triangle. - The mutual distances of more than three clocks can not be all equal when the clocks are placed on the same plane. - If the clock placed at A synchronizes with the clock at B and also with the clock at C, a fourth clock placed at D only synchronizes with clock A, B and C when clock A, B, C and D are placed at the vertexes of a tetrahedron. - (The setup requires the symmetry of A and B to both act as a light source and as a reflector from the start.)* This brings us to: §2 On Relativity of Lengths and Times.(page 4, second last alinea) -“We imagine further that at the two ends A and B of the rod, clocks are placed which synchronize with the clocks of the stationary system, that is to say that their indications correspond at any instant to the “time of the stationary system” at the places where they happen to be. These clocks are therefore “synchronous in the stationary system.” -“ To synchronize the clocks at two ends A and B of the rod in motion, it requires a second rod in the stationary system. At the two ends of the stationary rod clock C and D are placed. This creates a situation of two parallel rods of equal length and a total of four clocks necessary to make a balanced symmetrical comparison between a stationary rod S and a rod M in motion.* “We imagine further that with each clock there is a moving observer, and that these observers apply to both clocks the criterion established in § 1 for the synchronization of two clocks. “ The criterion established in §1 is: t B − t A = t ′A − t B .” (page3) “In agreement with experience we further assume the quantity to be a universal constant—the velocity of light in empty space. It is essential to have time defined by means of stationary clocks in the stationary system, and the time now defined being appropriate to the stationary system we call it “the time of the stationary system.” However if we apply the criterion established in §1 to 4 clocks on both ends of two stationary parallel rods, the following is valid: t B − t A = t ′A − t B = t D− t B = t ′B − t D = t C − t A = t ′A − t C and t B − t A = t ′A − t B ≠ t D − t A = t ′A − t D = t C− t B = t ′B − t C This means that even when both rods are stationary compared to each other, it is still impossible to synchronize all four clocks using Einsteins criterion. Thus the following statement is also untenable. “Taking into consideration the principle of the constancy of the velocity of light we find that where rAB denotes the length of the moving rod measured in the stationary system. Observers moving with the moving rod would thus find that the two clocks were not synchronous, while observers in the stationary system would declare the clocks to be synchronous.”, The observers in the stationary system do not declare the clocks to be synchronous. “So we see that we cannot attach any absolute signification to the concept of simultaneity, but that two events which, viewed from a system of co-ordinates, are simultaneous, can no longer be looked upon as simultaneous events when envisaged from a system which is in motion relatively to that system.” Even stationary events can only be looked upon as simultaneous events under the strict conditions I mentioned above. Temporarily conclusion: All the calculations in the next chapters of the KINEMATICAL PART concerning are based on a theoretically untenable thought experiment. Thanks to Strange for the link hermes.ffn.ub.es-luisnavarro-nuevo_maletin-Einstein_1905_relativity.pdf.webloc Alternative Simultaneity: Placed at a vertex of a stationary equilateral triangle, for the observer of clocks at the opposite vertexes these clocks run synchronized. Observers placed at the opposite vertexes of an equilateral quadrangle having sides c will experience shared simultaneity via two clocks placed at the open vertexes. Under the condition that AD < 2c or BC < 2c simultaneity is preserved for both observers independently of their relative velocity. The diagram allows a straight forward derivation of the Lorentz Transformation and does not need time dilation. Important is that this setup is expandable and independent from inertial motion. Pasted Graphic 2.tiff Pasted Graphic 1.tiff
-
Thanks Studiot and Strange.
-
I only found the German version. If you would be so kind?





_edited-1.thumb.jpg.a064c7f36b276d054699ee28447486a3.jpg)