Everything posted by zak100
-
problem with connecting with mysql
@Sensei Hi, I am able to create a user: mysql> create user 'pyuser2'@'localhost'identified by 'pyuser22' -> ; Query OK, 0 rows affected (0.01 sec) mysql> GRANT ALL PRIVILEGES on mysql.* to 'pyuser2'@'localhost'; Query OK, 0 rows affected (0.01 sec) mysql> Please guide me what should be the next step. Zulfi.
-
problem with connecting with mysql
Hi, I followed the link but I am getting error in creating user: mysql> create user 'pyuser'@'localhost'; ERROR 1819 (HY000): Your password does not satisfy the current policy requirements mysql> Somebody please me.
-
problem with connecting with mysql
@SenseiHi, Thanks for your response. I think I am getting garbage: When I use ping localhost, my output is: This is the first time, I am executing mysql with Python. I am working on Ubuntu 18.04. Somebody please guide me. Zulfi. 4 rows in set (0.00 sec) mysql>
-
problem with connecting with mysql
Hi, I am using pycharm to execute my program, I am getting following error: Process finished with exit code 1 Following is my code: import pymysql.cursors # con = pymysql.connect('zulfi'@'localhost' (password: NO)) conn = pymysql.connect(host='localhost', user='root', password='', database='db', charset='utf8mb4', cursorclass=pymysql.cursors.DictCursor) I have created "db" database in mysql: Somebody please guide me. Zulfi.
-
EVM tags and opcodes
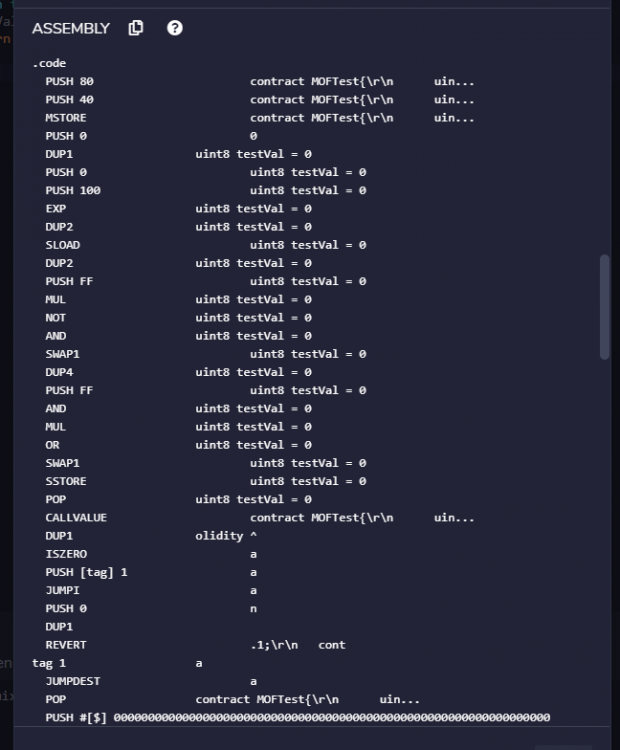
Hi, I want to understand the purpose of tags in EVM assembly and their relationship with Solidity function. pragma solidity ^0.5.1; import './Mod.sol'; contract MOFTest{ ModifiedBank mb; constructor(address payable addressOfBank, uint amount) public {} function deposit (uint amount ) payable public { } } I found that if I have a constructor then Remix IDE will have only 2 tags but now I have 2 functions and I found that there are 5 tags. Kindly explain me what is the purpose of tags and what is their relationship with Solidity functions? Also the tags are appearing in a haphazard manner, first tag1 and tag2 , then again tag1 and tag2, after that Remix IDE shows rag4, and then tag3 & tag5. I have attached an image image in this connection also related to the opcodes generated by the Remix IDE for the code shown above, sorry I can't scroll. Somebody please guide me. Zulfi.
-
Executing MAIAN tool: what is test.sol and where to store the retrieved Etherscan.io contract
Hi, <Did you not post on the forum about solidity before?> Yes, I posted about this also but no reply. <Did you not study it back then and take notes so you can write it now? > Never. But sorry why are you asking these questions? Are you against forums? You know this is the advantage of forums that we can learn from each other. I can't understand why are you feeling bad about this. If you don't know no problem. I am not pressing you to tell me. <I feel like you are spending way too much time on something that would be a lot easier if you got a cheap course. >goo I know about Solidity but I am not good at testing that's why I am posting. <I am not an expert in all this blockchain stuff. Surely there is one on Udemy etc but you will have to wait for a sale. > Okay no problem, let some other person reply me. But if I am in a position to afford anything, I don't wait for sales. Zulfi.
-
Executing MAIAN tool: what is test.sol and where to store the retrieved Etherscan.io contract
Maian Tool Repository: How to store contract retrieved from etherscan.io and what is ‘test.sol’ Hi, Hi, I am to execute the MAIAN tool from its repository on docker. The link at : GITHub Maian tool Issue The above link provided details of how to execute the MAIAN tool from docker. I am in the MAIAN tool repository on docker. They have first tried to access a smart contract from docker using Etherscan.io: Accessing smart contract using Etherscan.io The name of the contract is KaratBankCoin. They have not told where to store the contract. Later on they used the command: python maian.py -c 2 --soliditycode test.sol KaratBankCoin I am getting the error : ==================================================================================================== [ ] Compiling Solidity contract from the file test.sol ... [-] Contract file test.sol does NOT exist [-] Contract KaratBankCoin does NOT exist Because I don’t know what is test.sol and I don’t know how and where to store the KaratBankCoin contract retrieved from mainnet using Etherscan.io. They have not provided any details about test.sol and how to store KaratBanCoin because we are in the Maian tool’s repository. Somebody please guide me. Zulfi.
-
Installing web3 on Ubuntu 18.04
Hi @fiveworlds, Thanks a lot for solving my problem. God blesses you. You are right, it was related to Python: I pressed Alt-F12, to go into the terminal mode and then installed the web3.py using the following command. python3 -m pip install web3 Zulfi.
-
Python pycharm project: how to solve no web3 using CDN link
Hi, @Ghideon very good link. This can be useful for object oriented programming. @fiveworlds: Thanks, you have solved my problem. Actually it was related to python. When I installed web3.py using pip command the "no web3 module error" went away. Zulfi.
-
Python pycharm project: how to solve no web3 using CDN link
Hi, Sorry I don't mean web3.py. <That is a CDN for downloading JavaScript to run web3 on a webpage. Similar to jQuery you just need to use the <script> tag. But it won't be available to Python or NodeJS.> This is what I am talking about. By web3 I mean web3.nodejs. Its a javascript stuff. Kindly look at my following are posts: reddit web_js installation reddit_Ubuntu ethereum_stack exchange Sorry nobody is able to solve my 1 severe vulnerability problem related web3.nodejs Zulfi.
-
Installing web3 on Ubuntu 18.04
Hi, Can you please show me your results for "npm install web3"? They say that 'g' is used for global installation. I got following: $ nvm install node Downloading and installing node v15.5.0... Downloading https://nodejs.org/dist/v15.5.0/node-v15.5.0-linux-x64.tar.xz... ######################################################################### 100.0% Computing checksum with sha256sum Checksums matched! Now using node v15.5.0 (npm v7.3.0) zulfi@lc2530hz:~$ npm install web3 removed 1 package, and audited 353 packages in 1s 1 low severity vulnerability Some issues need review, and may require choosing a different dependency. Run `npm audit` for details. zulfi@lc2530hz:~$ I can't remove this problem: reddit web_js installation Please guide me how to get rid of this low severity error? Also have you tried to run smart contracts after installing web3.nodejs with -g option? Zulfi.
-
Tensor Flow Package Problem
Hi Sensi, Thanks for your response. I am using PyCharm under ubuntu 18.04. I would try to install anaconda and then report back. Zulfi.
-
Python pycharm project: how to solve no web3 using CDN link
Hi, Thanks for your response. I can't install web3.js on my ubuntu machine. I am getting "1 severe vulnerability problem". Is there any way to solve this problem by directing the link of web3 to a python repository? What is the meaning of the post in my first message? Zulfi.
-
Python pycharm project: how to solve no web3 using CDN link
Hi, I am trying to compile a python code on ubuntu 18.04: from __future__ import print_function from web3 import Web3, KeepAliveRPCProvider, IPCProvider import argparse,subprocess,sys At the end I am getting the error: I found one post which says: Can the above hint help me to solve the web3 module not found error? Please guide me how I can implement the above technique? Zulfi.
-
Tensor Flow Package Problem
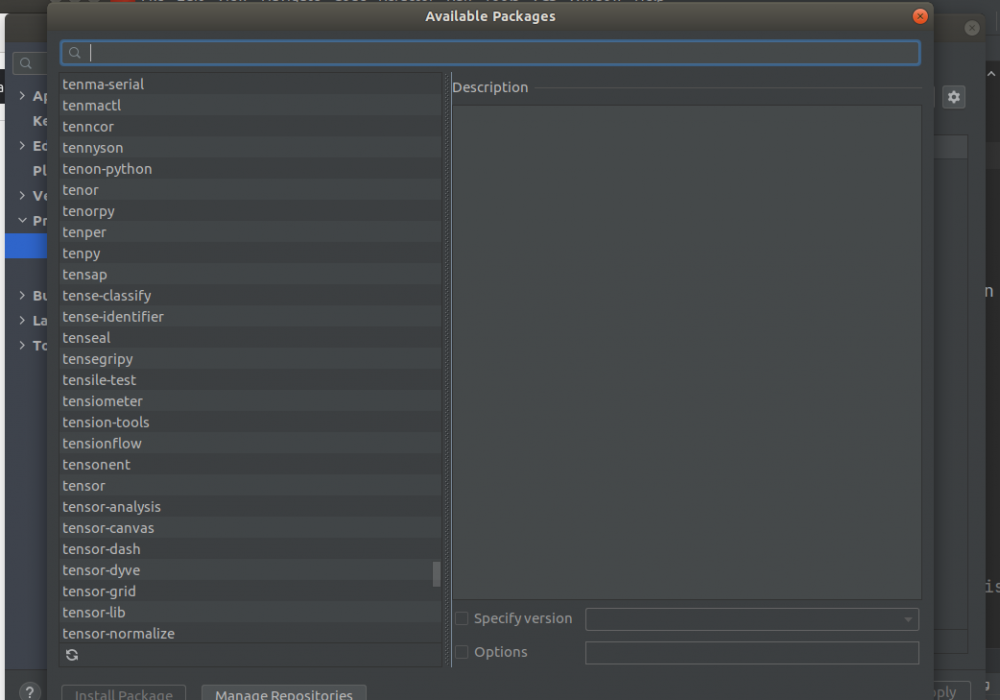
Hi, Thanks for your response. I followed that link but I cant see Tensorflow in the list of packages: Somebody please guide me. Zulfi.
-
Installing web3 on Ubuntu 18.04
Hi, I have installed nodejs on my ubuntu machine. I am trying to install web3 on my ubuntu 18.04 system. I am using the following command: @lc2530hz:~$ sudo npm install -g web3 but I am getting the error: sudo: npm: command not found But when I am typing: @lc2530hz:~$ npm --version 6.14.6 Kindly guide me how to install web3. I have got some solution here: https://askubuntu.com/questions/1301489/problem-with-installing-web3-using-npm But I don't know how to implement it. Somebody please guide me. Zulfi.
-
Tensor Flow Package Problem
Hi, Thanks for your response. The link is related to my post. I was able to install on the terminal. But I am using PyCharm. If I install anything on Terminal it will not become part of Pycharm. So I have to install the package within the Pycharm environment. Please guide me. Zulfi.
-
Tensor Flow Package Problem
Hi, I am getting "Tensor Flow" package problem. I am running the code on PyCharm community version3: I installed the package on the terminal: But still I am getting error, somebody please guide me. Zulfi.
-
Are the regular expressions same?
Yes. But why the regexp not working? Zulfi.
-
Are the regular expressions same?
Hi, \(S→Ad,A→aAa|bAb|c\ What I understand that 'd' is not allowed in the middle. Based upon this : \(S--> aSaS)\ \(--->bSbS)\ \(--->c)\ \(---->d)\ I think that the above rules are not correct because we can put 'd' in the middle. Please guide me. Zulfi.
-
Python: Finding the index of a substring in a string
Hi, Thanks. The correct concept is: ind = response.find("Your Email address)
-
Python: Finding the index of a substring in a string
Hi, I am trying to find out the index of a substring in a string. "in" tells that the string is present but "find" is returning -1. import numpy as np cnt = 0 response = "the following information: Your Email address." ind = "Your Email address".find(response) print("index =", ind) if "Your Email address" in response: print("Yes") Somebody please guide me how can I get the index of substring in the string. Following is the output: Zulfi.
-
Are the regular expressions same?
Hi, I am following the syntax of our teacher and he says that "U" is for union and it is same as "+" or logical "or" operator. I don't know what you mean by union. Sorry for not specifying this earlier. Please tell me what you guys mean by "U" in the context of regular expression? Sensei: I would try the calculator and then let you know. Zulfi.
-
Are the regular expressions same?
Hi, "Maybe you could clarify if actually wish to discuss regular expressions* or something else? " I am discussing about regular expressions. Its not programming/logic, its automata theory course. In my opening post "U" means the union, its same as "+" and I am talking about regular expression. "*" means zero or more repititions. I don't know about negative. "Also, just a friendly reminder; we are on a discussion forum, your short questions "please tell me", "please give examples" etc does not, in my opinion, promote fruitful discussions." Whatever information, I have I used to provide, i.e. code, images and expressions. If you need more information please let me know. Zulfi.
-
Are the regular expressions same?
Hi, Thanks for your response. Sorry ALine this is automata theory. Ghideon: Please tell me what you ean by one and two capturing groups? Sensei: Please give mme some example how the online debugger can help me to differentiate? (bba U aab)*= bba, aab, aab, bba ... or empty Can't we not have bbabbaabaab in the above regular expression? (bba)* U (aab)* = bba, bbabba, bbabbabba, empty, aab, aabaab Please tell me is my answer correct? Zulfi.