Mitko Gorgiev

Then read the thread once again. I have explained it. Why? Is there a rule that I cannot post a link to my thread? I think you give yourself too much power.

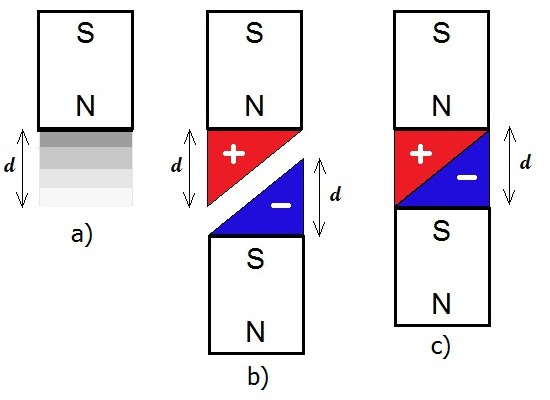
Let us consider some experiments. We place a stiff copper wire on a table. Parts of its length don’t touch the table. Above a wire section that does not touch the table we hold a strong cylindrical magnet with its plus-pole down (N-pole), so that the wire lies exactly under the middle of the magnet. Then we connect a new battery to the ends of the wire so that the plus-pole is closer to us and the minus-pole further away from us. At the moment of connection we will notice that the wire makes a strong deflection to the left and up. As soon as we turn the magnet over and repeat the same, the wire will make a strong deflection to the right and up. If we hold the magnet again with the positive pole down, now not directly over the wire, but left over it, however still close to it, we will notice that the wire after connecting to the battery makes a jerky movement to the right and down. How is this explained? In the first variant, the permanent magnet “blows” down; the magnetic wind in and around the wire blows clockwise spirally from the plus to the minus-pole of the battery; it blows down on the right of the wire, up on the left of it; on the right of the wire both magnetic winds coincide (the effect intensifies), and on the left of the wire they collide (the effect weakens); the wire moves to where the effect only intensifies, namely to the maximum, and that is to the left and up. In the third variant, in which both winds only collide, the wire deflects to where the adverse effect is maximally attenuated or quite ceased, namely to the right and down. What will happen if we place a second identical magnet below the first? The upper magnet will pull the conductor to the left and up, while the lower magnet to the left and down. The resultant force will be to the left, perpendicular to the magnetic lines of force (figure below). But this applies only if the conductor is placed exactly in the middle between the magnets and if the magnetic field is homogeneous. What is a homogeneous magnetic field? Please look at the drawing below (figure a): The magnetic field of the magnet is weaker at a greater distance from the magnet’s pole. At a greater distance than 'd', we could say that the strength of the magnetic field is practically zero. The weakening of the strength is symbolically represented by the different shades of gray. The weakening is also symbolically represented by the red and the blue triangle in the figure b. If the two identical magnets are brought at the distance ‘d’ (or lesser than ‘d’) without allowing them to come together, then in the interspace between them there is a homogeneous magnetic field because the two fields complement each other. This means that the strength of the magnetic field is the same in every point of the interspace (figure c). The magnetic field is homogeneous in terms of strength, but it is not homogeneous in terms of polarity. The Plus and the Minus retain their character just as before the bringing of the magnets close to each other. So, the Fleming’s left hand rule is valid only in one particular case, that is, when the conductor is placed exactly in the middle between the magnets. When a rule is valid only in one particular case, then it can be no rule at all. Therefore the Fleming’s left hand rule should go to the trash heap of the history. Consider also whether this formula about the so-called Lorentz force is true: F = qE + qv x B See also: A new explanation of the electric current

Yes, you have missed many things because you cannot solve a very simple task. I had to add only these sentences in my last post: In the red cross section of the figure (a) the current flows away from us and then enters the Plus-input of the oscilloscope (represented with the Plus-sign in the figures a and b). Therefore we get a positive voltage on the screen. In the blue cross section of the figure (b) the current flows also away from us and then enters the Minus-input of the oscilloscope (represented with the Minus-sign in the figures a and b). Therefore we get a negative voltage on the screen. WOW, what a number of attacks without any real argument against the things said in my OP. You all really got upset. Let's bet if you are so sure. How much would you bet? “All truth passes through three stages. First, it is ridiculed. Second, it is violently opposed. Third, it is accepted as being self-evident.” Arthur Schopenhauer

Since you cannot guess, I would say that the one who is clueless about electromagnetism is you. I will explain it to you tomorrow and answer to the other replies. It is pretty late in Macedonia. I have to go to sleep now.

Look please at the figure below: The red and the blue circles are cross sections of the two relevant sides of the rectangular loop. The two ends of the loop are connected to two slip rings. One slip ring is connected to the Plus-terminal of an oscilloscope; the other slip ring is connected to the Minus-terminal. Let's say we have colored the two relevant sides of the loop - one in red color, the other in blue color. In the figure (b) the loop has rotated 180 degrees with respect to its position in the figure (a). Can you guess what I am going to say next? How much would you bet? I will bet as much as you say. Dropping a magnet through a coil is completely different setup from a loop which rotates in a magnetic field. The time will tell. Just sit back and relax.

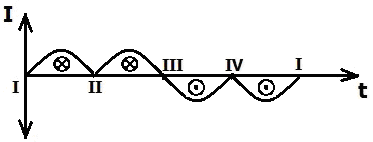
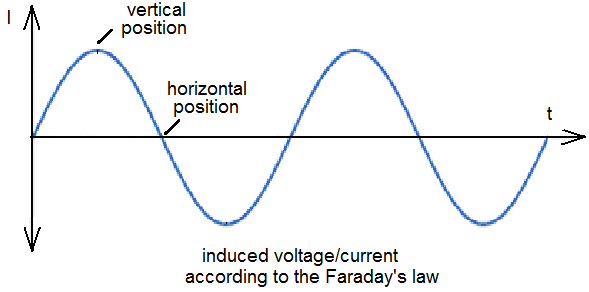
The first example including the sine curve is what the induced current would be according to the Faraday's law. It predicts a sine waveform whose maximum should be when the loop is in the vertical position (according to the first image of the rotating loop in my OP). I claim that in the vertical position of the loop the current will drop to zero. The current will also drop to zero when the loop is in the horizontal position. Therefore, we will not get a sine curve on the oscilloscope, but a curve as I draw it in my OP: The maximum(s) will be actually in the moments when the loop is in the position of 45 degrees. This is quite enough to disprove the Faraday's law. I don't have to do that experiment. I can conclude what the waveform of the induced current will be on the basis of much simpler experiments. If someone has the means to carry it out, let him do it. I bet that I am right. Would you bet that I am not?

Where am I asserting in the thread you have linked that the Maxwell's equations are not valid? More generally, what has that thread to do with this one? Moreover, do you have some objections against the things said in this thread? Otherwise, I would consider your replies as trolling.

If you mean this topic: https://www.scienceforums.net/topic/47901-faradays-law-is-false/ then I have to tell you that I have nothing to do with the man who has posted it ten years ago.

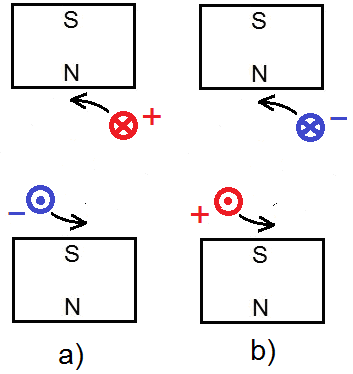
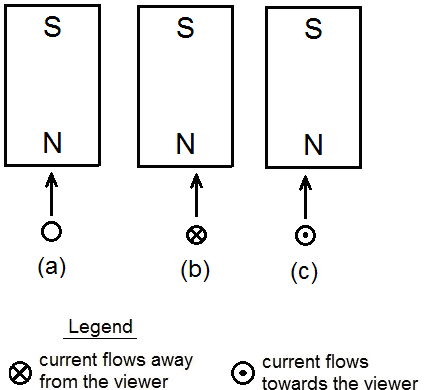
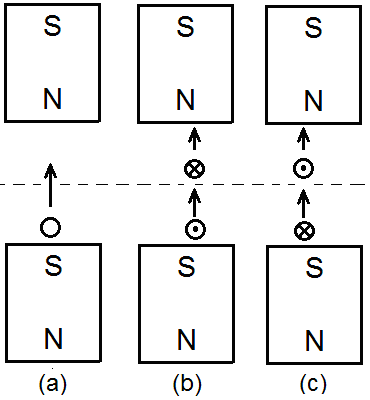
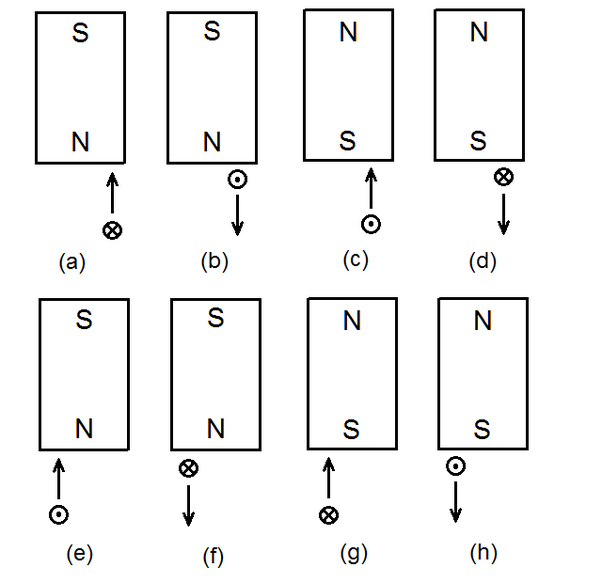
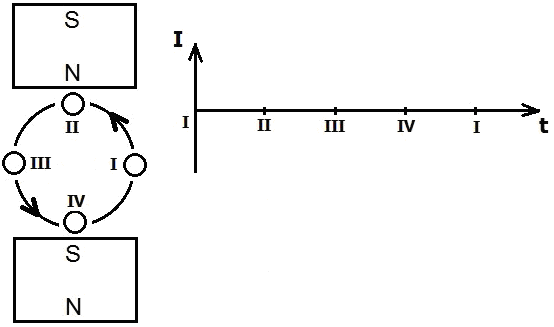
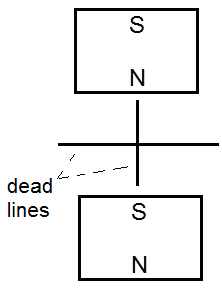
One of the fundamental laws of electromagnetism is the “Faraday's law of induction”. This law states that the induced EMF in a wire loop is equal to the rate of change of the magnetic flux enclosed with the loop, or E=dΦ/dt (the minus sign before “dΦ/dt” is left out because it is not important for our discussion). In the textbooks is often given an example of a loop in the shape of a rectangle which rotates in a magnetic field (figure below). What is meant by “the rate of change of the magnetic flux enclosed with the loop”? To explain this, we will make a comparison. If we hold a ring in front of our eyes as if we want to see through it, then it has a shape of a circle. If we turn it 90°, we only see a line. In every other intermediate position of the ring, we see an ellipse. In the first position, the ring has the maximum area in front of our eyes; in the second, the minimum, i.e., zero. If the ring starts to rotate about its axis starting from the second position (0) and has turned 180°, then the area we see in the course of this rotation can be represented with a sine curve of half a period. Similarly, when the wire loop is in the vertical position (according to the image above), then the magnetic flux is zero, and when the wire loop is in the horizontal position, then the flux is maximal. This flux changes according to a sine function, too. So, when the flux is maximal, then the rate of its change is minimal, more precisely, zero, because the slope of the sine curve in this point is zero. But when the flux is minimal, then the rate of its change is maximal, because the slope of the curve in this point is maximal. So, from the Faraday's law of induction it follows that when the wire loop is in vertical position, then the induced current in the loop is maximal; and when it is in horizontal position, then the induced current in the loop is zero (graph below). If we connect the ends of the wire loop to an oscilloscope, would we really get this curve?!! Let’s consider the following experiment. From a lacquered copper wire we cut off twenty to thirty pieces of about 10 cm. From them we form a bundle of parallel wires and connect the two ends with one more wire each. The other ends of these two wires are connected to a sensitive analog ammeter. We hold the bundle horizontally and move quickly a strong and broad magnet downwards on its left side. The pointer of the instrument will make a deflection to one side. If we now move the magnet quickly downwards on the right side of the bundle, the instrument will make a deflection to the opposite side. The magnetic flux that we have produced in the wire is now in the opposite direction to the one in the first case, which is why the deflection is in the opposite direction. The motion of the magnet produces current even if we only approach it to the bundle from one side without lowering it below the bundle. In this case the current is somewhat weaker. But if we now move the magnet down to the middle of the bundle, the instrument won’t show any current, because the left and the right halve of the magnet act on opposite sides of the bundle, canceling each other out. We can do the experiment with only a single wire instead of a bundle, as long as we have a very strong magnet and a very sensitive ammeter. You can imagine that inside this wire there is a propeller or there are many propellers in a row. When you turn a propeller manually from the left side, then it is turning in one direction and it is blowing on one side (plus), but it is suctioning on the other side (minus). When you turn the propeller from the right side, then it is turning in the contrary direction and the air current is in the opposite direction. But we cannot turn the propeller from above. Exactly the same picture we have with the magnet and the wire. After we have lowered the magnet down and have produced a current in one direction, then we can move it back upward. In that case we produce a current in the contrary direction, just as we will produce an air-current in the contrary direction if we turn the propeller(s) from down up. Whether the magnet is moving toward/away from the wire, or the wire is moving toward/away from the magnet, there is no difference. Therefore, let us consider the following experiments. A straight conductor is moving vertically exactly toward the middle of a magnet. No current is induced in this conductor (figure a below). In the second variant (figure b) the conductor is shifted 1 millimeter to the right and is moving again vertically toward the magnet. A current is induced in it which flows away from us. In the third variant (figure c) the conductor is shifted 1 mm to the left and is moving vertically toward the magnet again. A current is induced in it which flows toward us. Consider now this experiment: a straight conductor is moving vertically exactly in the middle between two identical magnets [ figure (a) below ]: No current is induced in this conductor. In the figure (b) the conductor is shifted 1 millimeter to the right and is moving again vertically from the lower to the upper magnet. A current is induced in this conductor. But during its movement upwards, the induced current changes the direction. To the dashed line, which is exactly in the middle between the magnets, the induced current flows toward us. When the conductor is exactly in the middle, the current drops to zero. Then, above the dashed line, begins a current flow in opposite direction. In the figure (c) the conductor is shifted 1 millimeter to the left and is moving again vertically from the lower to the upper magnet. A current is induced in it, but here the reverse happens with respect to that of the figure (b). Why is this happening? Please look at the drawing below (figure a): The magnetic field of the magnet is weaker at a greater distance from the magnet’s pole. At a greater distance than d, we could say that the strength of the magnetic field is practically zero. The weakening of the strength is symbolically represented by the different shades of gray (figure a). The weakening is also symbolically represented by the red and the blue triangle in the figure (b). If the two identical magnets are brought at the distance ‘d’ (or lesser than ‘d’) without allowing them to come together, then in the interspace between them there is a homogeneous magnetic field because the two fields complement each other. This means that the strength of the magnetic field is the same in every point of the interspace (figure c). The magnetic field is homogeneous in terms of strength, but it is not homogeneous in terms of polarity. The Plus and the Minus retain their character just as before the bringing of the magnets close to each other. (I call the pole of a compass, which points North, the Plus pole. I will post soon a topic considering this question). Please look at the figures below: Here are presented all the eight possible variations of a conductor moving toward and away from a magnet. Consider the first (a) and the last (h) variation. These two variations were unified in a single experiment in the second-to-last figure above (figure b). But what happened there? The current induced in the conductor dropped to zero exactly in the middle between the magnets. How so? Because the Plus and Minus are of the same strength in that point. Therefore they cancel each other out regarding the electromagnetic induction. Please look now at the figure below. A straight conductor is rotating uniformly counter-clockwise in a homogeneous magnetic field according to the figure above. The rear end of the conductor (that which is farther away from us) is connected to the positive terminal of an oscilloscope, the front end to the negative. What will the graph of the induced current (/voltage) look like? Please look at the picture below: There are two crossed lines in it, which I call “dead lines”. Whenever the conductor moves through one of these lines, there is no current induced in it. Therefore I have named them “dead lines”. But in reality these dead lines are dead planes. The horizontal plane I call the main middle plane. Which plane is represented by the vertical line? It can be any vertical plane which goes through the central point between the magnets (that is, the cross point in the diagram above). But which one out of the infinite number of them? That depends on the direction of the conductor. Let’s say that the rotating conductor is positioned exactly in the North-South direction. In that case the vertical plane is also in that direction. So, when the conductor is rotating in a homogeneous magnetic field as in the figure above, the induced current will be zero in the four points marked with the Roman numbers (graph below). When a rectangular loop is rotating in a homogeneous magnetic field, then we have in fact only a second identical conductor which rotates diametrally to the first, because only these two sides of the loop play a role in the induction of the current (marked with “L” in the figure below). Since the current in the second conductor has a contrary direction, the induced current in the loop will be twice as strong (recall that it is a loop.) The graph above is valid also for this loop, only we have to draw the waveform twice as high. So, the Faraday’s law of induction is not true because it predicts a wrong result. I believe (and that is not without grounds) that Michael Faraday has never defined this law. He was a great experimentalist and he would have made many experimental trials before definitely defining something. I rather believe that this law has come among the people through the third of the Maxwell’s equations and somebody has called it so in honor of the great Faraday. You may ask yourself: Is that equation really true?

There are already many questions and objections to my OP. English is not my mother language and I cannot express myself very fast. So, be patient, I will try to answer all the questions. Yes, it is said that it is circular. But it is also said that those circles are at 90 degrees with respect to the wire line. In another word, perpendicular. STUDIOT says: If you don't see the point, maybe somebody does. To what experimental observation does it run counter? Yes, I need a conductor to have an electric current. If you refer maybe to the vacuum tubes, then they are only a small part of the conducting path. The greater part consists of metal wires. The quotation from Oersted bears no relation to my post ?! I think you haven't read my post carefully. Here is my paper for those who want to see the experimental evidence: LINK DELETED

Is this a threat? I have also other things to do than answering questions. My post is not even half a day on this forum and I have already got threats. In the time of Giordano Bruno you would have probably burned me. I will answer all the questions one by one.

Contemporary physics doesn't assert that the magnetic field is perpendicular to the current carrying wire??? I have seen many, many textbooks on physics where this is said. Yes, I can make quantitative predictions, but the post would have been much longer. I don't understand this question. I have many experiments which support my theory. They are presented in my paper which is downloadable free of charge. I don't understand how it contradicts my assertion. Can you elaborate? Why is a stranded wire so different from a solid wire? The electric current is immaterial and the type of wire (whether it is stranded or solid) doesn't play a role.

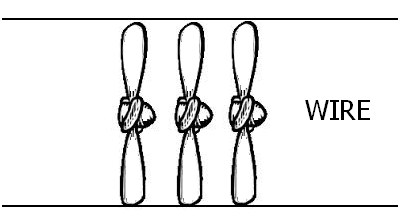
Electric current is an immaterial swirling wind through the electrical conductor. The immaterial magnetic wind through it is also spiral-shaped (i.e., it is not perpendicular to the conductor as the contemporary physics asserts). During the flow of direct current, both winds blow from the plus- to the minus-pole of the battery, the electric wind in counter-clockwise direction, whereas the magnetic wind in clockwise direction. These two fluxes are at angle of 90 degrees. I will introduce a new explanation of the electric current which I call “dynamic” because it speaks of forces (δύναμις = force), in contrast to the contemporary explanation which is materialistic, because it speaks of material particles, called electrons, supposedly moving through the metal wires. I call the new explanation “dynamic” because in its basis lies vibration of electromagnetic forces (EM-forces). These forces are not material. What was just said is well documented when we recall that the magnetic and the electric forces cannot be blocked by material bodies that are placed between the source of the force and the bodies they act on. For example, if we put a piece of iron near a magnet, the magnet will attract it even if we place a plastic, wooden or metal board between them. Likewise, radio waves penetrate walls without perforating them. This can be done only by something that is not of material nature. But even though they are immaterial, a material body is needed as their source. And in order to manifest themselves, they also need a suitable object to act upon; otherwise we would not be aware of their existence. Other terms necessary to understand the new explanation are “order” and “orientation”. We can get a notion of these terms from several things: from magnetism, thread, wood, etc. When a magnet is brought in the vicinity of iron powder, the particles of the powder will adhere to the magnet with strictly oriented order. If we think of such a particle as a very small line segment, then it aligns itself not only in the same direction with the other particles, but also has a strict orientation of its plus and minus poles. We can imagine the particle as the smallest possible line segment and yet its properties will remain as described. In the thread we also have an ordered multiplicity of tiny little plant or animal fibers in the same spiral direction, except that there is no orientation here, that is, the fibers have no poles. Now I will introduce the electromagnetic force element, which is the basis of the explanation. It has the following form: The EM-force element has three segments. In the middle is the magnetic segment with its two poles, M(+) and M(–), and at its ends are the electrical plus (E+) and minus (E−) segments, arranged at an angle of 90° to the magnetic segment. We have to imagine this element in a huge multiplicity, evoked by the power source. [ In relation to this new explanation, we could also visualize a new notion of the matter: if we, so to say, descend ever deeper and deeper in the matter, at the end we come to nothing. But this “nothing” is actually not nothing. It is invisible, intangible, immaterial forces: electromagnetic forces, light forces etc. The matter at the end, so to say, “dissolves” in immaterial forces. So, we could say that the matter is a kind of condensation of immaterial forces. ] Let’s say the power source is an electrochemical cell, i.e., a battery. What is a battery? If two plates of two different metals (say copper and zinc) are partly immersed in a dissolved agent (acid, base, salt), then the part of the copper plate outside the liquid is polarized in one sense (plus), the immersed part in the opposite sense (minus). For the zinc plate applies the opposite. Plus means blowing, minus means suctioning. The two metal plates of the battery can be imagined as two fans. The one that blows outside the liquid (positive electrode = copper), that suctions inside the liquid; the one that suctions outside the liquid (negative electrode = zinc), that blows inside it. When the electrodes are connected with a metal wire, a closed flux is created. The plus is the strongest near the positive pole and, as we move away from it through the wire, its strength continuously decreases. The same applies to the minus, but starting from the other pole. Figuratively, we can represent it this way: So, the current that emanates from the copper plate is a plus current, because we usually speak of the current through the connecting wire. The current from the zinc plate is a minus current. Just as the air wind from a fan is a swirling motion, so it is the electric wind through the conducting path. And just as the air swirl is more extended when the air current is stronger, so it is the electricity’s swirl when the electric current is stronger. But as the electricity’s swirl is becoming more extended with increased electric current, so the magnetic swirl, or rather, the magnetic spiral is becoming more compact (i.e. lesser extended). When the current is stronger, then the magnetic spiral is so tight, that it is practically at an angle of 90° with respect to the conductor’s line; but, of course, never ideally. At the same time the electricity’s spiral is practically at an angle of 0° with respect to the conductor’s line. Here we have something very similar to the water swirl and its cavitation. When a propeller is turning underwater, then the motion of the water is to one direction, while the motion of the cavities is at angle of 90° with respect to that of the water (drawing below). The faster the propeller is turning, the more extended is the water swirl and the more compacted is the cavities’ spiral. The motion of the water corresponds to the motion of the electric wind; the motion of the cavities corresponds to the magnetic wind. Please watch these two short YouTube videos (the first from 2:22): https://youtu.be/DDsPag56GQE?t=144 https://youtu.be/Y7k7p1RirkI Although the electromagnetic element is represented by straight lines, it is only a symbolic representation. Each line represents a flux, and the many elementary fluxes unify themselves in a single electromagnetic flux (principle of self-similarity). The E and M-segments could be imagined as helical gears. Probably it seems inconsistent that we draw the EM-force element so that the arrows of both E-segments point from their sources outwards on the one hand, while on the other hand we say that the one force has a suctioning effect. Hence, its arrow should have been drawn in the opposite direction. However, the direction of the arrows does not refer to whether the force acts from the source outwards or inwards, but rather to the effect of the action of both E-segments on the M-segment, that is, on its righting with respect to the wire line. Quotation from Hans Christian Oersted (21 July, 1821): “All the effects on the north pole above-mentioned are easily understood by supposing that negative electricity moves in a spiral line bent towards the right, and propels the north pole, but does not act on the south pole. The effects on the south pole are explained in a similar manner, if we ascribe to positive electricity a contrary motion and power of acting on the south pole, but not upon the north. The agreement of this law with nature will be better seen by a repetition of the experiments than by a long explanation. The mode of judging of the experiments will be much facilitated if the course of the electricities in the uniting wire be pointed out by marks or figures.” Quotation from Michael Faraday (1822): “The theory of M.Oersted, therefore, seems to require that there be two electric fluids; that they be not either combined or separate, but in the act of combining so as to produce an electric conflict; that they move nevertheless separate from each other, and in opposite spiral directions, through and round the wire; and that they have entirely distinct and different magnetical powers; the one electricity (negative) propelling the north pole of a magnet, but having no action at all on the south pole; the other electricity (positive) propelling the south pole, but having no power over the north pole. I have before said, that I am not able to comprehend the whole of the Professor's statement, and, perhaps, therefore, ought not to send you any account of it. It is to be hoped, however, that this celebrated philosopher will shortly develope the principles more at large, which have already led him to the results he has published; and there can be no doubt that in pursuing them he will arrive at other results as new to the world, as important to science, and as honourable to himself, as those he has already made known.”