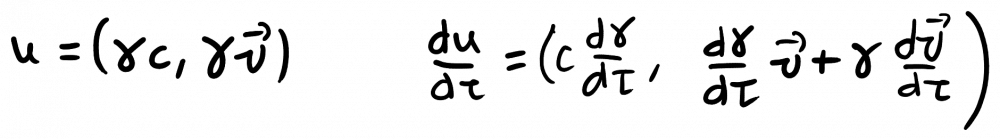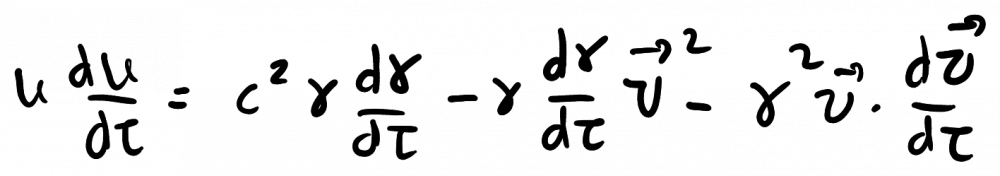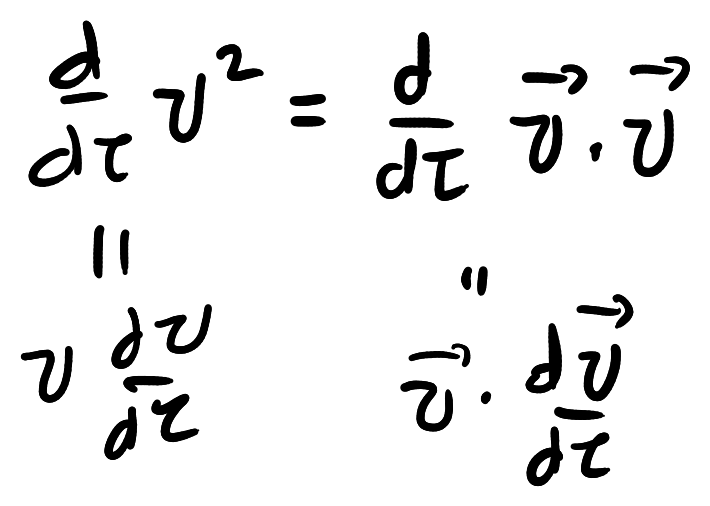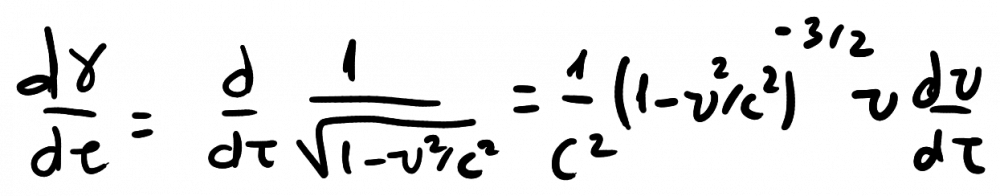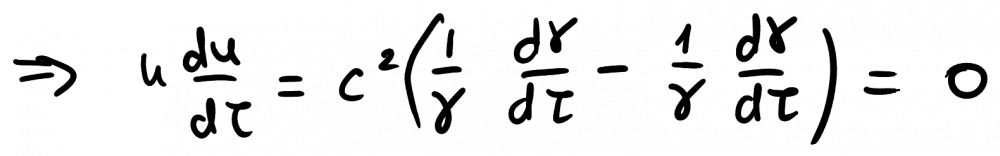-
Posts
4785 -
Joined
-
Days Won
55
Content Type
Profiles
Forums
Events
Everything posted by joigus
-

Has Ockham's Razor become blunt in the last 700 years ?
joigus replied to studiot's topic in General Philosophy
Sorry, I'm not familiar with it. I agree that the OP has a point, even when applied to science. But I still think it all has to do with the scope of what you want to explain, with what we could call first principles vs particular explanatory pathways based on those principles. In the spirit of what @Prometheus says, there are overarching principles (simple), and then there is the implementation of particular scenarios (complicated parametrics). Something like that. I want to make more comments. Perhaps later. I need some sleep. The discussion is tantalizing. I feel a bit behind the game right now. Maybe I'm just tired. -

Has Ockham's Razor become blunt in the last 700 years ?
joigus replied to studiot's topic in General Philosophy
Ockham's-razor rule of thumb rests on two simultaneous optimisation desiderata: 1) Maximum simplicity. 2) Fitness to account for observation. The search for maximum simplicity works under the constriction to fit experimental data. The latter overrides it all. If explanations seem more complicated it's likely because the range of phenomena that we intend to contemplate is widening more than ever before. Further constrictions operate on approximations, ancillary hypothesis, etc., to account for an ever more complicated landscape of phenomenology. I tend to agree with the points as expressed by @CharonY, @Ken Fabian, and @Prometheus even though I cannot be totally sure that we would completely agree with each other in the finer details. Summarising, I think Okham's razor is alive and well, even though it's become subtler and more difficult to apply it. -
Yes, I've noticed that. Seems like all of our comments have gone unanswered. I think I've noticed a pattern though. After a couple of posts he even stops addressing the person. I wonder what that means...
-
I don't know how to interpret the fact that the OP has decided not to address my comments at all.
-
To add to the panoply of excellent comments by Kino and Markus, you cannot expect an arbitrary linear combination of 4-vectors to be a physically significant 4-vector. Both vectors must be timelike \( \left(u_{\left(i\right)}^{0}\right)^{2}-\boldsymbol{u}_{\left(i\right)}\cdot\boldsymbol{u}_{\left(i\right)}\geq0 \) and orthochronous \( u_{\left(1\right)}^{0},\:u_{\left(2\right)}^{0}>0 \). Also, the resulting 4-vector must be normalised to \( c^2 \). In that sense, when you're working with 4-velocities, you're not working on a plain linear space --Minkowski space--, but in some kind of "unitary quotient of it." This distinction is referred-to in physics by means of the buzzwords "on-shell" and "off-shell." Adding vectors off-shell can lead you to vectors on-shell, and vice versa. This point has arisen before --Ghideon has been particularly persistent. Off the top of my head, you can derive a common (CoM) 4-velocity for 2 material particles moving every which way by calculating the common 4-momentum, and then dividing by \( m_1+m_2 \) --which are relativistic invariants. Another thing you could do is calculate the centre-of-energies motion and then impose that it be normalised as to become a physical 4-vector. One last thing you could do is use Einstein's addition of velocities --which doesn't involve the masses--, to obtain a physical 4-vector, by multiplying by the appropriate observer-dependent factor as to obtain a 4-vector. I don't know. I'm just trying to help you so that your effort is not in vain. So far, it is in vain, simply because you're not distinguishing with any care what's on-shell and what's off-shell.
-
Thanks for telling us, @studiot. I'm sorry. I'd like to reach out to everybody who has a genuine interest on what all of this (reality) is about, no matter what their background or what their grasp of science is. We as individuals come and go, but the human endeavour to understand the cosmos and ourselves, and how all that we perceive came to be, lives on. My homage to Mike, I will express in the words of Ticho Brahe, as I remember them referred by Carl Sagan --addressed to Johannes Kepler: "Let me not seem to have lived in vain."
-
Hope this helps.
-
Hats off to Ghideon. Great summary.
-
I'm no expert either, so be my guest. And of course it would be nice that some of the local experts can give us a hand. Yes, DNA does get old. That's at the basis of cellular aging, and thereby the organism's aging itself, AFAIK. The replication mechanism is some kind of bi-directional zip assembly, so it's always imprecise at the ends. In one direction the replication process is very smooth, because the initial fragment (RNA primer) and the DNA polymerase work in the 5' to 3' direction, but in the opposite strand, primer and polymerase are forced to work against the uncoiling of the double strand, so it must interrupt and restart the copying work over and over again --the so-called Okazaki fragments. That's why there's always a mismatch at the end. Eukaryotes use a meaningless[?] chunk of DNA at the end --telomere-- which is partially replenished with every replication process, to kind of delay this ongoing degrading of the information. Also, as you point out, different cells down the line of cellular development, have different adjustments to their particular function. Red blood cells being the perfect examples of cells that will never go back to be able to produce anything in the way of stem-cells or higher-potent cells, because they've completely lost their DNA. Other extremes are neurons and cells from the digestive lining. The average life of the latter is, if I remember correctly, 48 to 72 hours. And neurons, because they never get replenished by sister cells mitotically splitting. Although new neurons do appear directly from stem cells, especially in the hippocampus*. Also, they retain some ability to reconnect, or change connections. That's about the summary of what I know. * Google search: "newborn neurons in hippocampus and olfactory bulb"
-
Suspicious of anyone? Eek!
-
That goes for neurons. But I meant it --more in general-- in the sense that the cell --every cell, including neurons-- is the basic unit that carries out a particular function within the organism. In order to do that, they specialize down the line of cellular development. Cells have a finite life though, so when they no longer work, they are replaced by releasing stress signals that activate their destruction and further mitosis in other sister cells. As long as the cell is performing its function, it's important that it does it well --cancer being an example of how bad it is that a cell stops working properly. Cancer cells get stuck in continual mitosis and just can't stop. It's their function that's essential. Gametes, on the contrary, are some kind of "inter-phase" between one organism and the next generation. They carry random arrangements of half the genetic material --haploid cells-- of the parent organism; and they're fundamentally like a throwing of the dice. Not a functional cell really. Not yet. So chromosomes are expendable. On the contrary, the organism cannot afford to have malfunctioning DNA in the nucleus of working cells. That's why eukaryotes have mechanisms to destroy tissue cells that are not working properly. It doesn't play around trying to fix it --replace it. During replication cells do have an impressive proofreading mechanism, very precise --transcription and translation don't have to be that accurate--. But when DNA that's being read for transcription is just too messed up, the cell must be destroyed. When the cell malfunctions, the DNA is replaced... by replacing the whole cell. Not taking any chances. But a gamete turns bad? No problem for this organism. That's more or less what I meant.
-
But, as I understand, in common slang "dark side of the Moon" means the side that we never see from Earth. Although it's not always dark. Ergo: misnomer. I think it was Eric the Red who decided to call it "Green land" so that his fellow Vikings would buy into the idea of going there looking for pastures new. May be an apocryphal story.
-
An alternative proof from direct Taylor expansion in the metric coefficients and counting how many parameters are left that I cannot set to zero by changing the coordinate system: https://www.youtube.com/watch?v=gf-G4QiAHLY&list=PLaNkJORnlhZnwjIXnOHrX50FEyoyiTh4o&index=5 Those must coincide with the number of independent components of the Riemann. \( \frac{1}{12}n^2\left(n^2-1\right) \) Uses Young tableaux, which allows you to count free parameters very easily.
-
Oh, but that's not because it's much worse than I pointed out. It's because it's bound to get worse if you make a notational blunder of that magnitude. If you want to discuss anything in terms of a 2-index tensor being diagonal in a certain point --o perhaps everywhere?, the OP didn't tell us--, you could arrange to distinguish this by using Latin capital letters, e.g., \[A^{BB}=\frac{\partial x^{B}}{\partial\bar{x}^{\mu}}\frac{\partial x^{B}}{\partial\bar{x}^{\nu}}\bar{A}^{\mu\nu}\] Meaning, \[A^{00}=\frac{\partial x^{0}}{\partial\bar{x}^{\mu}}\frac{\partial x^{0}}{\partial\bar{x}^{\nu}}\bar{A}^{\mu\nu}\] \[A^{11}=\frac{\partial x^{1}}{\partial\bar{x}^{\mu}}\frac{\partial x^{1}}{\partial\bar{x}^{\nu}}\bar{A}^{\mu\nu}\] etc. So it can be done, but not the way the OP is doing it. Not that it's very useful to consider tensors as objects that are or aren't diagonal in any invariant geometrical sense, as they are objects referred to two different bases. Absolutely. When I'm doing maths and I get to such surprising results as "the whole of tensor algebra/calculus is bonkers, because all tensors are null" --or something like that, I'm not completely sure if that's the point--, I try to retrace my steps and, sure enough, I can spot a silly mistake. The last thing that would cross my mind is to highlight the "result" and announce to the world, "hey, I've found an enigma".
-
Sorry. I made a mistake here. The delta tensor is an isotropic tensor only when it is a once-covariant, once-contravariant tensor --similarly for tensor products of them--. And the epsilon tensor is an isotropic tensor only when it's totally covariant or totally contravariant. I already pointed this out in a previous post. Same OP. Different thread.
-
Yes, this surfaced in the 1st post already. Yes, that's another problem. But also, the OP is not familiar with tensor algebra. They have a tendency to use repeated indices both for summation convention and for representing fixed diagonal elements, so no wonder the conclusions are wrong, already just at the mathematical level. Also, I've observed them being very cavalier in asserting other properties about tensors. Symmetric or antisymmetric only make sense for tensors twice covariant or twice contravariant, etc. The delta tensor, or tensor products of delta tensors; and the epsilon tensor, or tensor products of them--, are isotropic tensors only when they are pure-covariant or pure-contravariant. And so on. Seeing tensor algebra used like this brings tears to my eyes. That's why I'm taking certain distance from this particular OP's posts. I'm only too glad I have you and Kino to help with this.
-
The OP wants to fix the value of the alpha index and at the same time keep Einstein's summation convention. Very dangerous practice. No wonder they get inconsistent results.
-
Exactly. I can barely add anything significant. Contraction of pairs of symmetric indices with pairs of antisymmetric indices always gives zero, no matter what the value of the non-zero components of both. The OP clearly has problems with the tensor formalism. \[ A_{\alpha\beta}=-A_{\beta\alpha}\] \[ S_{\alpha\beta}=S_{\beta\alpha}\] \[ Q=S^{\alpha\beta}A_{\alpha\beta}=S^{\beta\alpha}A_{\alpha\beta}\] (swapping dummies) and, \[ S^{\beta\alpha}A_{\alpha\beta}=\left(S^{\alpha\beta}\right)\left(-A_{\alpha\beta}\right)=-Q\] (applying symmetry properties) As \( Q=-Q \), \(Q\) must be zero, even if \( A_{\alpha\beta} \) and \( S_{\alpha\beta} \) are not. The rest of the indices are along for the ride.
-
I share your concern, but I'm an optimist. I think --or wanna think-- many people will realise that either we learn to fork out some attention span on reliability of information, or else we become too vulnerable, and we're done for. Even fish will take the bait for so long. After a while they know it's bait. Either they wise up, or only the cleverer survive. Although you're the expert angler here, Moon.
-
Not that I know of. You do have a section to test your LaTeX beforehand, as you already know: https://www.scienceforums.net/forum/99-the-sandbox/
-
Yeah, nice insight. \( \gamma^{-1} \frac{d\gamma}{d\tau} \) doesn't have to be zero, even though \( \gamma^{-1} \frac{d\gamma}{d\tau} - \gamma^{-1} \frac{d\gamma}{d\tau} \) is identically zero. Welcome to the forums, @Kino.
-
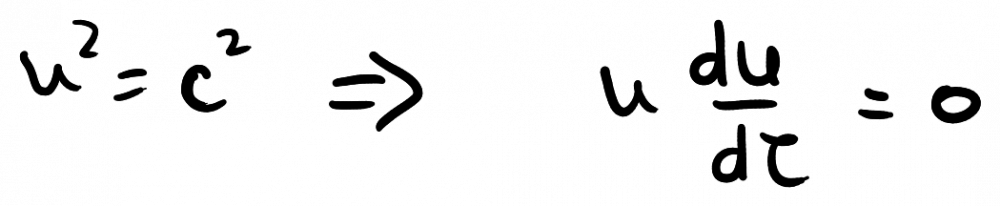
You may be right. I'm not following this thread very closely, and I'm not sure if what you say is what the OP is trying to prove. But here's a more standard proof: This is obvious, but let's do a check. And gammas, of course, are in general time-dependent. SR can deal with accelerations, as Markus said. The 4-vectors are, and their 4-product is, It's necessary to keep in mind that, The derivative of the gamma is, So the 4-product is indeed identically zero: As Markus also said, the concept that in SR supersedes constant acceleration is that of hyperbolic motion. He also has been very careful to distinguish flat space-time from prescription to adopt inertial frames. Indeed, the Minkowski spacetime can be studied in terms of Rindler charts --hyperbolically accelerated frames--. It is not difficult to show that when the motion is completely collinear (spacial 3-vectors of velocity, acceleration, and force). It's in wikipedia, although the proof is not complete, and I can provide a completion, if anyone's interested. As I said, I'm not completely sure that what I'm saying is relevant to the discussion. It is the standard, reliable, mainstream formalism that we know and love.