joigus

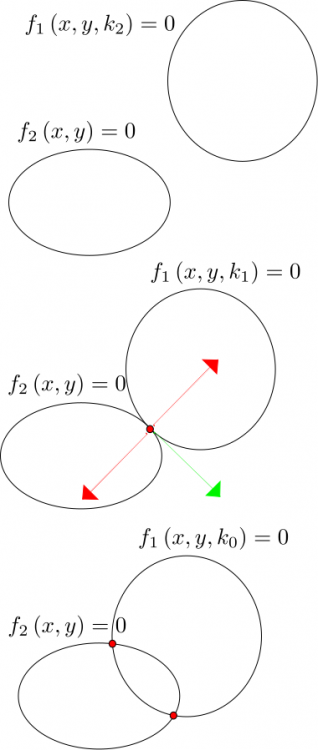
OK. I see what you mean much more clearly now. There's still something you've understood that I haven't. Problem is I don't have much time now, but I promise to get back. This was gonna be my drawing: There's an idea that maybe could work for the general case. I don't know. I'll get back to you ASAP. It's to do with the green and red arrows in the drawing. The co-tangential condition can be written as, \[\boldsymbol{\nabla}f_{1}\wedge\boldsymbol{\nabla}f_{2}=0\] It involves the determinant, \[\left|\begin{array}{cc} \frac{\partial f_{1}}{\partial x} & \frac{\partial f_{1}}{\partial y}\\ \frac{\partial f_{2}}{\partial x} & \frac{\partial f_{2}}{\partial y} \end{array}\right|\] It could work in the general case. I don't know. The problem is \( k \) doesn't appear there. Let's keep talking. No time now.

Mmmm. I think I know what you mean now. When you said you obtained the solution you were looking for, did you mean (in the 1st, simpler, example)?: \[ x = 5 \left( 1 ± \sqrt{1- \frac{3}{125} k} \right) \] \[ y = 6 \left( 1 ± \sqrt{ 1- \frac{1}{45} k} \right) \] \[ K ≤ \frac{125}{3} \] Can you show me in more detail how you got to that by your method of adding a third equation? The equation you propose is, \[\left(-2x+10\right)-\left(-4x+20\right)=0\] That gives \( x = 5 \) as only solution, and I don't see how that relates to what you're looking for. Your 'tangency' idea got me confused, especially in combination with the Jacobian. Maybe I can't help you after all, but I think I'm closer to understand you and hopefully offer you some insight.

Here you have some help: The Jacobian is a matrix, not a simple derivative. I still don't understand why you want to apply derivatives when your equation can be solved exactly. Neither do I understand how an equation derived from the previous one gives you more information. I'm still missing it. I'm sorry. Maybe somebody else can help.

Can you be a bit more explicit about what you're doing there? Are those partial derivatives, implicit (as in \( \frac{d}{dx}=\frac{\partial}{\partial x}+\frac{dy}{dx}\frac{\partial}{\partial y} \). Do they involve K as a function of x and y, or as an independent variable? There are several ways to take the derivative with respect to x, and some of them are sorely wrong. E.g., are you considering, \[x,\:y\left(x\right),\:K\left(x,y\right)\] or, \[K,\:y\left(x,K\right),\:x\left(K\right)\] perhaps? And why would you want to involve a further equation which is implied by the previous two and contains, if anything, less information? I'm missing something in your argument. By the way, I made a mistake. It's, \[K\leq\frac{125}{3}\]

Because, as I told you, the non-linear system, \[− x^2 +10x − \frac{1}{2} y^2 +6y − K=0 \] \[− 2 x^2 +20x+ \frac{3}{2} y^2 − 18y=0\] decouples into, \[5y^{2}\text{−}60y+4K=0\] \[5x^{2}-50x+3K=0\] Which is trivial: \[x=\frac{50\pm\sqrt{2500-60K}}{10}\] \[y=\frac{60\pm\sqrt{3600-80K}}{10}\] Only solvable under the bounds, \[K<\frac{250}{6}=\frac{125}{3}=41.\overline{6}\] \[K<\frac{360}{8}=45\] The lowest upper bound being, \[K<\frac{125}{3}\]

Only if the energy-momentum source is spherically symmetric.

No general rule in non-linear equations. This system is particularly simple because it's a 'scrambled' set of quadratic equations in x and y. You can un-scramble it easily, find the conditions for K, and overlap.

I am. For starters

How significant is the Arizona flip?

You're welcome.

The answer is no, there is no particular point of origin. But that doesn't mean we can always map every point from within our chart. In general we need local charts, which are restricted patches of coordinates. Take the sphere as an example: You cannot map the whole sphere with one smooth coordinate system, though there is no particular point in the sphere that requires you to leave it out of the coordinate patch because of any geometric distinction. Yes AFAIK, as long as there is nothing physical that requires a singularity (e.g., static, non-rotating black holes.) Not necessarily, although arguments of symmetry force you to consider coordinates that take into account the centre of the gravitating object if you want to describe a wide-distance range of phenomena. But in fact, when you want to describe test particles crossing the horizon, more convenient coordinate patches are advisable than those distinguishing the centre of attraction. Coordinates around the centre of crossing.

Your constraint is F(x,y) = 1. Defines an implicit function y(x). As F(x,y) = sinh(x+y)/xy, there you are.

Can you do ordinary polynomial integrals and derivatives? Give me something. What is it you don't know?

Indeed. A bunch of massless particles can in principle generate curvature. Indeed. The acceleration parameter the OP is talking about refers to time-space relative curvature. Indeed. Intrinsic geometry are the key words, as Janus suggested. Indeed. No velocity there, just dilation, measured by expansion parameter. Indeed. Only energy-momentum, as said. Indeed. Action at a distance is no longer accepted as accurate. Indeed. m=0, v=c. Period. Indeed. It's not an easy theory. A cylinder appears 'bent' to you --as @Janus said-- only because you're looking at it as embedded in a 3-dimensional space. But a cylinder is actually flat.

Good idea. That's the ticket. OK. I've been racking my brain for quite a while. And the reason is there is no hyperbolic-trigonometry relation that gives you equality between, \[\frac{y\sinh\left(x+y\right)-xy\cosh\left(x+y\right)}{\cosh\left(x+y\right)xy-x\sinh\left(x+y\right)}\] --for which you've applied correctly the chain rule--, and, \[\frac{y-\cosh\left(x+y\right)}{\cosh\left(x+y\right)-x}\] which is the simpler expression you will find if you follow @studiot's tip. And the reason for that is that, if you want to find the simpler expression --Studiot's and your book's--, you must use the constraint given: \[y'=\frac{y\sinh\left(x+y\right)-xy\cosh\left(x+y\right)}{\cosh\left(x+y\right)xy-x\sinh\left(x+y\right)}\] \[xy=\sinh\left(x+y\right)\] along your curve. So that, \[y'=\frac{y\sinh\left(x+y\right)-\sinh\left(x+y\right)\cosh\left(x+y\right)}{\cosh\left(x+y\right)\sinh\left(x+y\right)-x\sinh\left(x+y\right)}=\] \[=\frac{y-\cosh\left(x+y\right)}{\cosh\left(x+y\right)-x}\] Consequently, your derivative was correct, but you must use the constraint once again if you want to get to the final expression that's in the book. I hope that's clear. It would remain for you to prove the simpler expression directly by using Studiot's tip. It's not difficult. I just wanted to dispel the "paradox."

You forgot to derive \( x+y \) using the chain rule in the first \( \cosh \). Edit: No, wait a minute. You didn't. I think the book "means", \[y'=\frac{y\tanh\left(x+y\right)-xy}{xy-x\tanh\left(x+y\right)}\]

I don't know what the status of the question is, but this is exactly the part I didn't understand at all. It seems like Tina is reconsidering and I on my part think everybody is being considerate and trying to understand the problem. Not at all, @wtf. I think you understand it better than anybody else here. At least than me. I applaud your suggestion to start with simpler numbers.

Effects depend on the amount of exposure.

At what point are you stuck? Can you parametrize a curve? Can you calculate components of curl or calculate div? Do you even know what they are?

I think I'm guilty of introducing an element of confusion here. You can set up Moontanman's though experiment with pretty much everything at rest. With an equidistant point C waiting for the signals to arrive, as Swansont said, I think. Then someone pointed out the relevance of question 'how do you define synchronicity between departures?' or something to that effect. I think that's key, because if C is at rest and planet A and B synchronize their clocks so as to depart at the same inertial time, there is no paradox. Paradoxes would appear if observers passed through C with different constant velocities, because in that case they would record A in the past of B or viceversa depending on the relative motion. I'm trying very hard not to be sloppy and not saying anything already covered. but I will have to look into this in more detail later. Well, paradoxes... You know what I mean. Yeah, I think it was Ghideon when mentioning 'relativity of simultaneity'. So the scenario in the simplest possible case is like Janus describes, I think. Everything is quite symmetrical and there is no paradox, but A and B must sync their clocks, and C musn't move with respect to them.

I'm sorry to hear that too, Ahmet. In my case, the workload has gone up and up. All this feels very strange. All the best.

Yes, it was a joke, but I meant something relevant to the discussion, I hope. What I meant is that the category 'scientist' has no closure, because it's a real category, so it's defined by family resemblance. It has no logical closure. Is this guy an astronomer?: https://en.wikipedia.org/wiki/David_H._Levy I think he is. By the same token, he is a scientist. It doesn't matter whether he is an academic or not.

Interesting noises are coming from the LHCb 'beauty' experiment. Analysis of angular data in decay B+→K*+μ+μ- reveal a 'tension' between the data and predictions of bare Standard Model. It seems that the results appear at the level of corrections via virtual particles. https://lhcb-public.web.cern.ch/Welcome.html (My emphasis.)

Michelle Pfeiffer is not a cat. But she has intersections with the category 'cat' that go beyond the costume.